群平行(相似)多列线
如何检查两条线是否接近平行?它们不必完全平行,但应该是相似的,因为它们的方向是相同的。
@Edit
我想我需要更多地解释每件事背后的想法。作为输入,我得到了许多多行。我想要做的是将多条线组合在一起,它们是相当平行的(一般都是相似的方向)。结果将是一组相似的多谱线。
多线看上去怎么样。它们一般向上或向左或向右。不需要从相同的y值开始。多角线的点一般不在同一高度,这就意味着y值不同。由于多条线通常是在某个区间内平行的,然后开始不同,我想找出区间边界,并在这个区间中定义多条线的部分平行线。当然,间隔不应该太小。
我现在将举例说明我希望取得的结果。从4条折线开始,P1到P4以蓝色显示。对于人类来说,很明显,在红线b1之前,P1-P3线是相当平行的。因此,这可能是第一组平行多线G1。在红线b1之后,有平行的多线P1和P4。因此,他们建立了小组G2。多线P3与其他任何东西都不平行,因此在组G3中是唯一的。希望那个插图能帮上忙
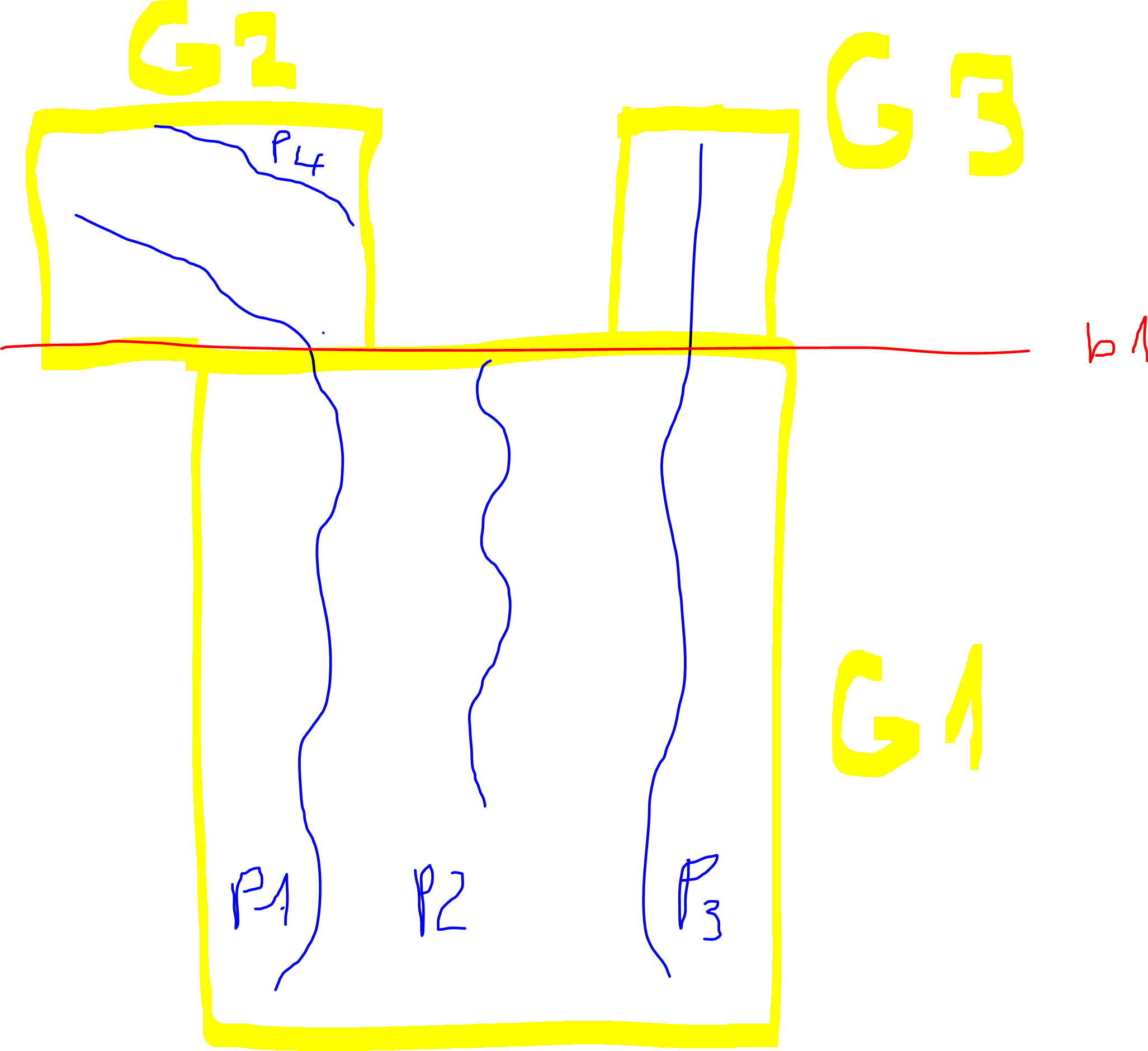
应该声明为并行的两条多线的示例:
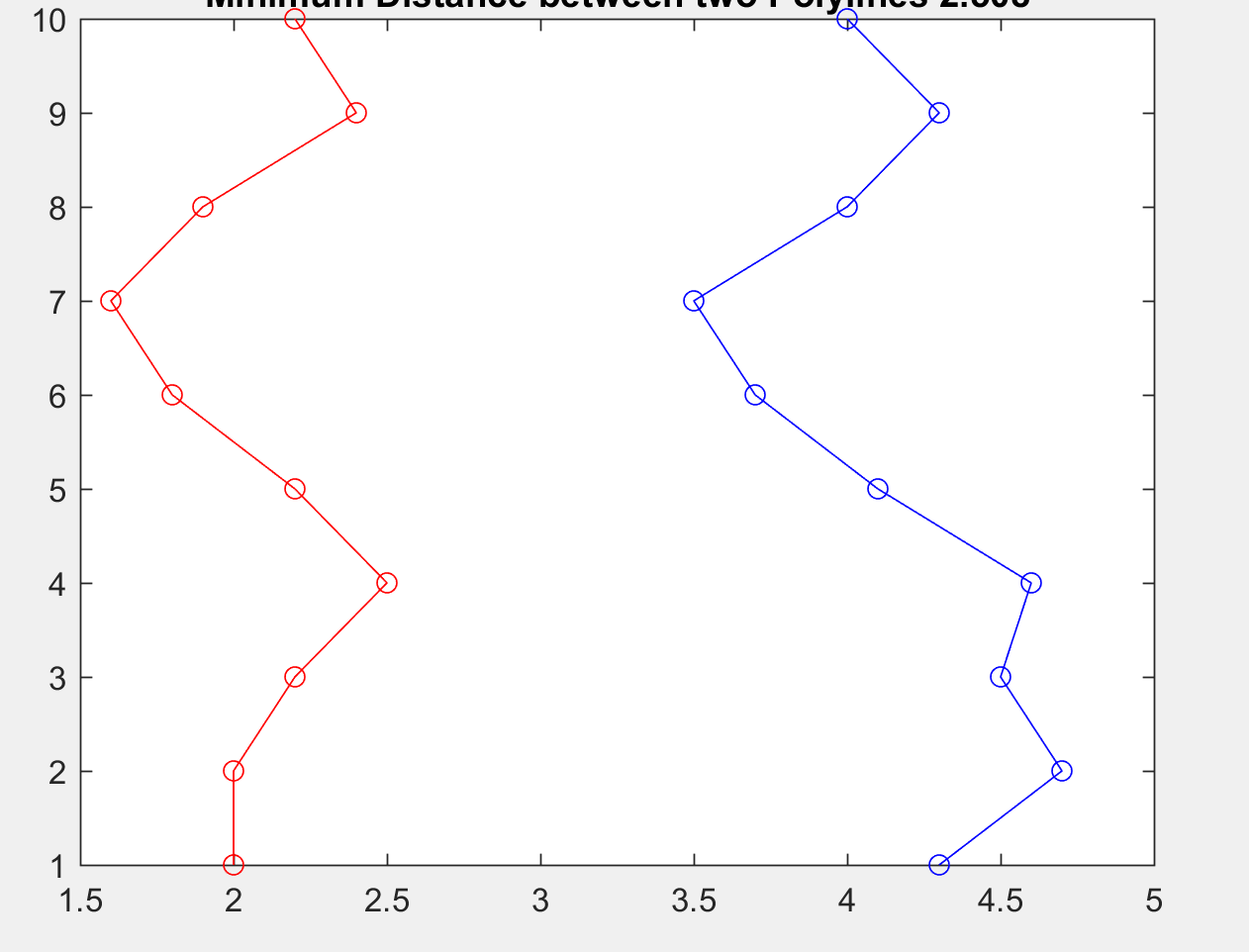
。
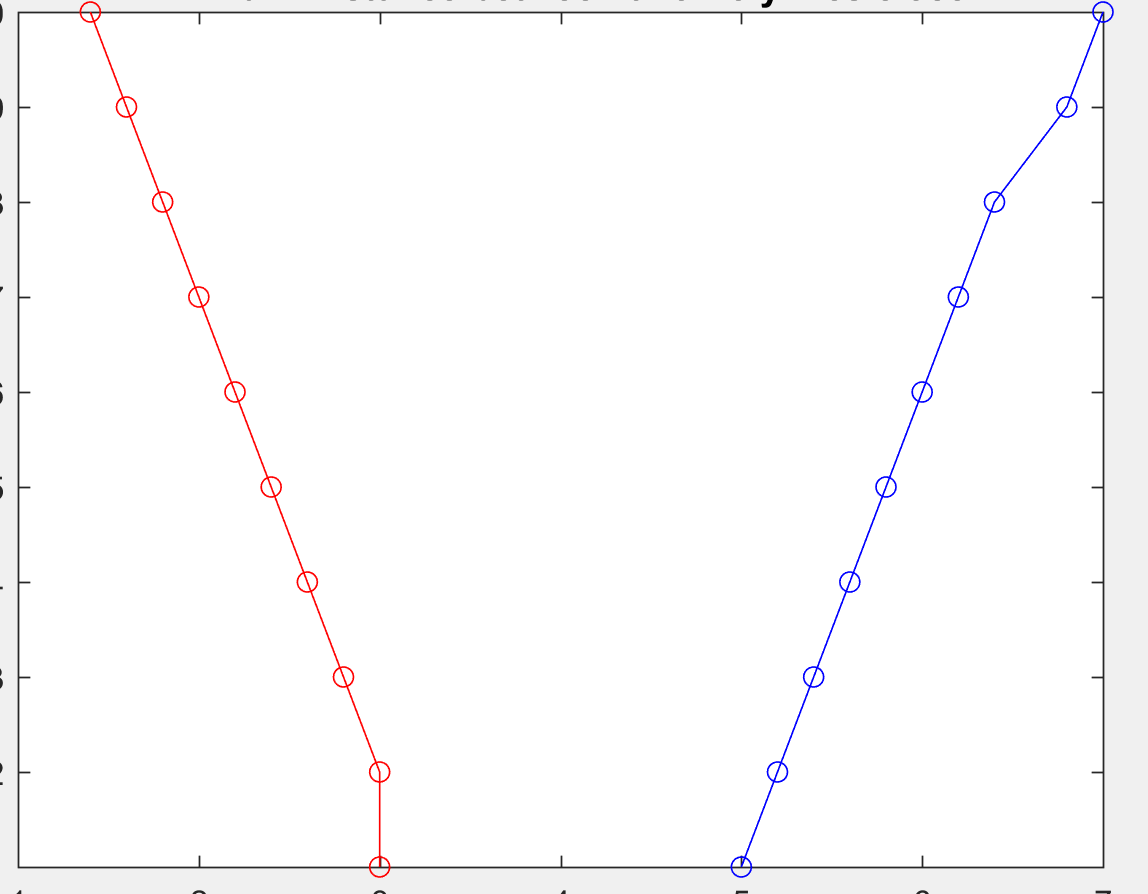
两个应该声明为而不是并行的多线的例子
@Edit 2在将douglas算法应用于输入多行后,得到了这个结果。现在我想把平行的多条线组合在一起。如何找到要比较的相应行段?此外,正如您在图“如何比较段”中看到的那样,多行1和2只应在间隔b1,b2中分组。我怎么才能找到这个间隔?这实际上意味着我需要找出要比较的部分。如果我比较它们,如果它们不是平行的,我将它们归类为不平行。如果它们是平行的,我仍然需要找到它们平行的间隔,对吗?那是因为一条折线可以开始和结束另一条。
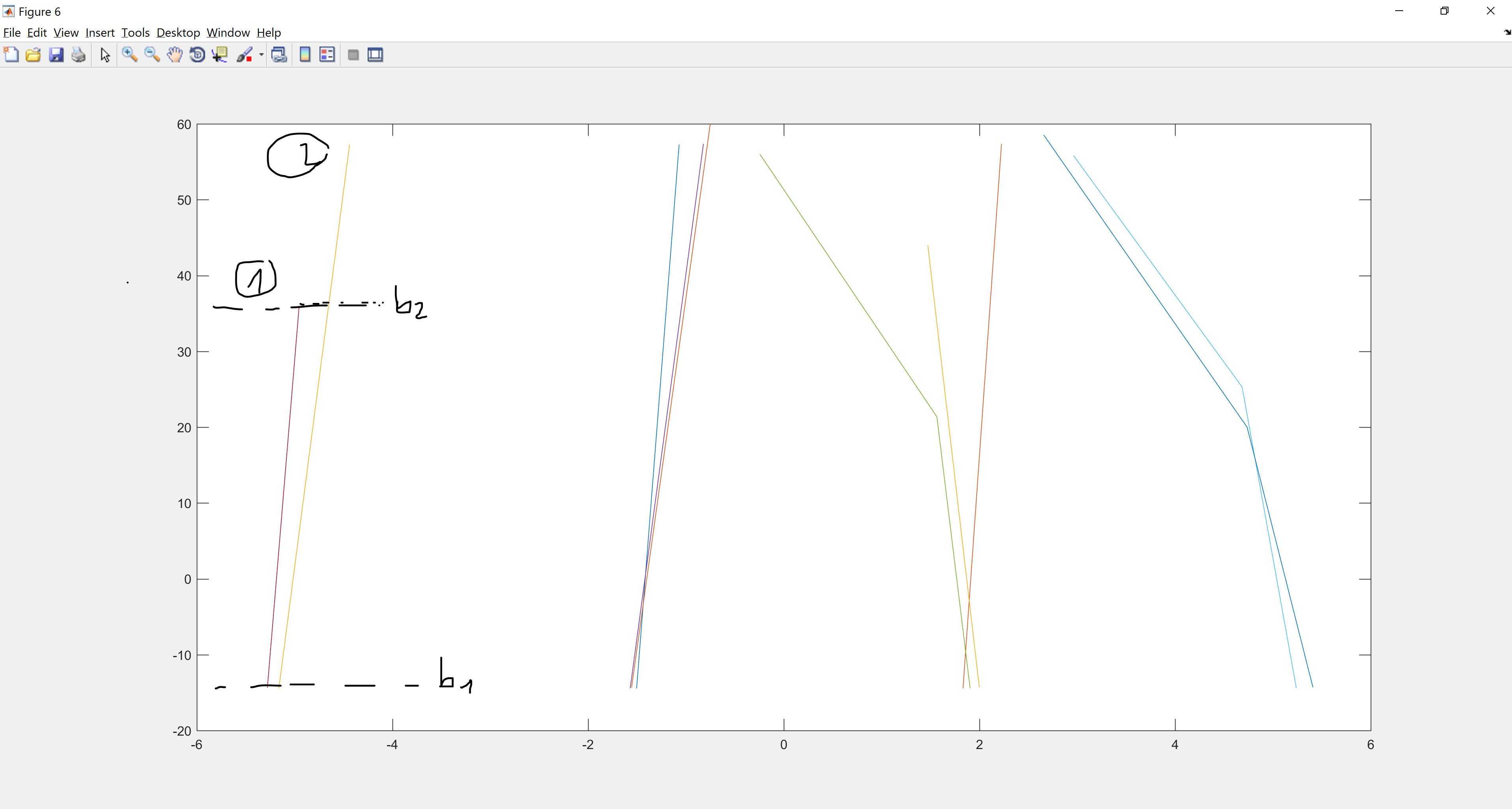
回答 4
Stack Overflow用户
发布于 2016-12-02 10:23:17
首先,拒绝任何交叉口。
然后对这些线进行线性回归。为“大致平行”设定一个阈值。现在选择一条折线,从最合适的线取最遥远的点(如果是终点,选择下一个点)。现在在“最佳匹配”点上分割另一条折线(基本上用一点斜度来保持距离,以使局部偏差最小,并在可能的情况下在拐角点上切入)。
重复,直到没有一个线段是多线,并应用相当大的距离和方向阈值。
Stack Overflow用户
发布于 2016-12-02 10:50:46
对于多边形A上的每个顶点,找出B上最接近的点,并输出这两个点之间的距离。(相反,使用最接近的顶点可能会很好。)对于A,对B也这样做。
现在对找到的距离进行线性回归。你应该得到一条水平线,大约。定义此检查的阈值。
Stack Overflow用户
发布于 2016-12-02 10:55:06
在您的示例中,您知道每一对线段共享y轴坐标,因此这些是索引,而且每个示例的线条都是连续的。
每个端点(y坐标)上的两条线之间的距离是已知的。因此:
for y in 0:n
delta_x[y] = abs(blue_x[y] - red_x[y]) 然后,如果从所有这些曲线中减去最小的delta_xy,就会有一条非负的曲线,这条曲线下的面积将与你的直线的平行程度成正比。
面积越小越平行,
越多面积越少平行,
完全平行没有区域。
但只有你可以选择你的门槛。
https://stackoverflow.com/questions/40929237
复制相似问题

