问最短公共SuperSequence

EN

让

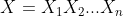
是字符串1和

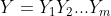
是字符串2。

设S是由X和Y as序列组成的任意最短超序列。让我们尝试创建这样一个序列。

很明显，X作为序列存在于S中，因此，最初S可以显示为：

​

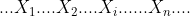
注：“……”这意味着空间可以是空的，也可以用来将Y的字符放入其中，使之成为由X和Y组成的最短超级序列。

这是最小值。我们只需要将Y的最小字符注入到这个S中，使它成为由X和Y组成的最短超级序列。另外，注意Y需要作为子序列而不是子字符串出现。因此，如果我发现Y的任何序列也发生在X中，那么这些字符就不需要被注入。

因此，我们证明了，要使for _s是最小的，就必须注入Y的最小特征，这样Y才能作为序列出现。为此，我们找到了X的最长序列，它也出现在Y中，换句话说，就是= LCS(X，Y)。

*=x_++(_

现在，存在多个LCS(X，Y)。取任意并构造序列。

首先，查看您发送的第二个链接，就可以创建一个超大的序列，其大小为:x，y，x，x，x。

对于两个输入序列，可以很容易地由最长的公共子序列(lcs)形成scs。

所以现在剩下的就是证明它实际上是最短的公共超序列。假设相反，假设有一个最短的公共超序列，使得它的长度为x，LCS(X，Y)-1 == X+区Y-(X(X，Y)x+ 1)。但是在这个字符串中，X作为子序列，Y作为子序列。这意味着它们在用字符串的大小来判断的{##**$$}(X，Y)x+1位置中相交。即存在一个大小为LCS (X，Y)x+ 1的LCS，这与LCS的定义是矛盾的！

因此，它的大小正好是{x，x，y}\x，y，x，x，y，x，xq.e.d

因为您只关心字母的计数，所以可以对所有序列(X、Y、Z和LCS(X，Y) )进行排序。这是因为排序序列(在计算出最小的内容序列和LCS之后)将保持字母的计数不变。

如果您正在考虑排序序列，您只需要考虑由一个字母组成的序列。这是因为每个序列中每个字母的计数独立于每个序列中所有其他字母的计数。

如果你只考虑由一个字母组成的序列，那么很明显，包含X和Y作为子序列的最小序列将是X或Y，而LCS(X，Y)将是另一个序列。因此(对极小包含序列采用符号"MCS“)，x-MCS(X，Y)x+x-LCS(X，Y)x=x-x-+y-x-x+y.