在Matlab中优化大量的函数调用
我正在用Matlab2016b中的fsolve()为每个体素数据集中的每一个体素解一对非线性方程。
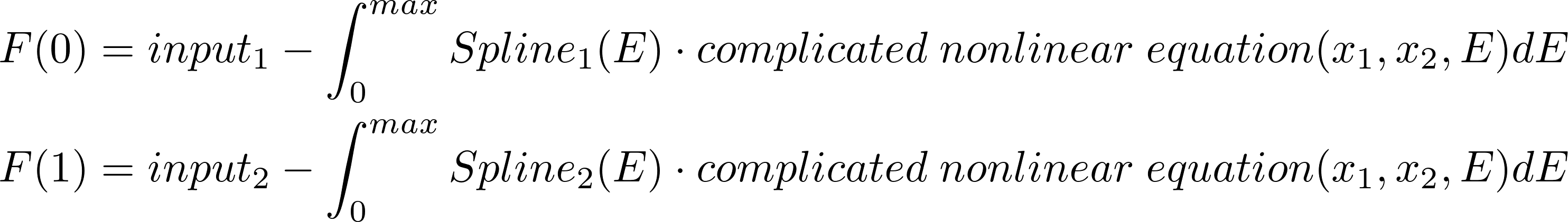
我已经完成了我所知道的所有“容易”的优化。内存定位是可以的,我使用的是parfor,方程的数值形式非常简单。积分的所有不连续点都被输入integral()。我使用了Levenberg-Marquardt算法,它具有良好的起始值和合适的起始阻尼常数,它平均收敛于6次迭代。
我现在每个体素大约有6毫秒,这是好的,但还不够好。我需要一个数量级的降低来使这项技术可行。在开始提高准确性之前,我能想到的只有几件事:
该方程中的样条用于复杂方程的快速采样。每个方程有两个,一个在“复杂的非线性方程”中。它们代表两个方程,一个具有大量的项,但光滑且无间断,另一个近似于从谱中提取的直方图。正如编辑建议的那样,我正在使用griddedInterpolant()。
是否有更快的方法从预先计算的分布中取样点?
parfor i=1:numel(I1)
sols = fsolve(@(x) equationPair(x, input1, input2, ...
6 static inputs, fsolve options)
output1(i) = sols(1); output2(i) = sols(2)
end在调用fsolve时,我使用Mathworks建议的‘参数化’来输入变量。我有一种唠叨的感觉,为每个体素定义一个匿名函数在这一点上占据了很大一部分时间。如果是这样的话,是否存在一次又一次定义匿名函数的相对较大的开销?我有任何方法将对fsolve的调用矢量化吗?
有两个输入变量不断变化,所有其他输入变量都保持不变。我需要为每个输入对求解一个方程对,所以我不能使它成为一个庞大的系统,并立即解决它。对于求解非线性方程组,除了fsolve之外,我还有别的选择吗?
如果不是,一些静态输入是相当大的。是否有一种使用MATLAB的persistent将输入保持为持久变量的方法,这会提高性能吗?我只看到了如何加载持久变量的例子,如何才能使它们只被输入一次,而以后的函数调用将不受大输入的巨大开销的影响?
编辑:
完整的原始方程如下所示:
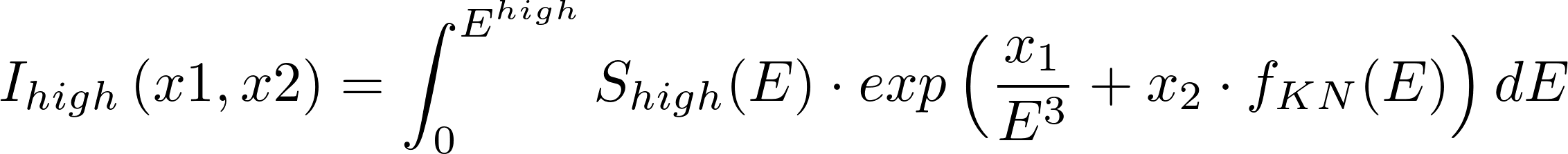
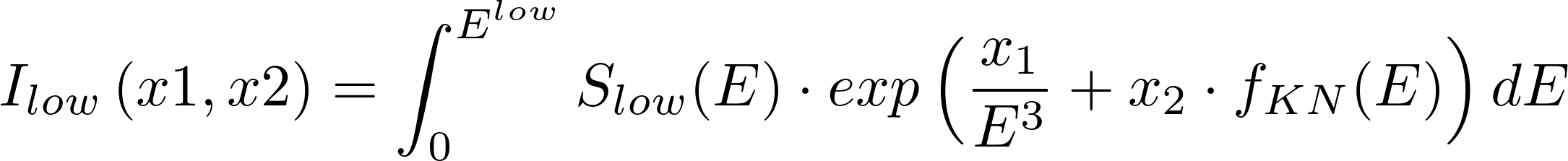
其中:
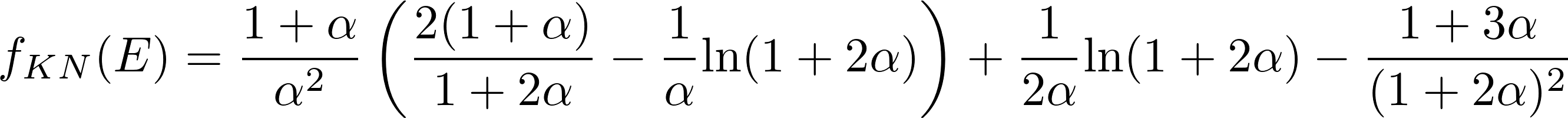
以及:
其他一切都是已知的,求解x_1和x_2。f_KN是用样条逼近的。S_low (E)和S_high(E)是样条,它们的直方图看起来如下:
回答 2
Stack Overflow用户
发布于 2017-01-12 11:19:07
所以,我想到了几件事:
查表
由于函数中的积分不依赖于x以外的任何参数,因此可以从它们生成一个简单的2D查找表:
% assuming simple (square) range here, adjust as needed
[x1,x2] = meshgrid( linspace(0, xmax, N) );
LUT_high = zeros(size(x1));
LUT_low = zeros(size(x1));
for ii = 1:N
LUT_high(:,ii) = integral(@(E) Fhi(E, x1(1,ii), x2(:,ii)), ...
0, E_high, ...
'ArrayValued', true);
LUT_low(:,ii) = integral(@(E) Flo(E, x1(1,ii), x2(:,ii)), ...
0, E_low, ...
'ArrayValued', true);
end 其中Fhi和Flo是计算这些积分的辅助函数,在本例中用标量x1和向量x2进行矢量化。将N设置为内存允许的高度。
然后将这些查找表作为参数传递给equationPair() (这允许parfor分发数据)。那么只需在interp2中使用equationPair()
F(1) = I_high - interp2(x1,x2,LUT_high, x(1), x(2));
F(2) = I_low - interp2(x1,x2,LUT_low , x(1), x(2));因此,与其每次重新计算整个积分,不如对预期的x范围进行一次评估,并重用结果。
您可以指定使用的插值方法,默认情况下是linear。如果您真正关心的是准确性,请指定cubic。
粗/细
如果由于某些原因(内存限制,以防x的可能范围太大)而无法使用查找表方法,那么您可以做的另一件事是:将整个过程分成两个部分,我称之为粗和细。
粗方法的目的是非常快地改进您的初始估计,但可能不是那么精确。到目前为止,逼近该积分的最快方法是通过矩形法:
- 不要用一个
S来近似spline,只需使用原始的表数据(所以S_high/low = [S_high/low@E0, S_high/low@E1, ..., S_high/low@E_high/low]) - 在
E的值与S数据(E0,E1,.)使用的值相同时,在x处计算指数: Elo = linspace(0,E_low,numel(S_low));integrand_exp_low = exp(x(1)./Elo.^3 + x(2)*fKN(Elo));Ehi = linspace(0,E_high,numel(S_high))‘;integrand_exp_high = exp(x(1)./Ehi.^3 + x(2)*fKN(Ehi)); 然后使用矩形方法: F(1) = I_low - (S_low * Elo) * (Elo(2) - Elo(1));F(2) = I_high - (S_high * Ehi) * (Ehi(2) - Ehi(1));
然后,为所有的fsolve和I_high运行这样的I_low和I_high,您的初步估计x0可能会改进到接近“实际”收敛的程度。
或者,使用trapz (梯形法)代替矩形方法。稍微慢一点,但可能更准确一些。
注意,如果(Elo(2) - Elo(1)) == (Ehi(2) - Ehi(1)) (步长相等),则可以进一步减少计算的次数。在这种情况下,两个积分的第一个N_low元素是相同的,因此指数的值只会在N_low + 1 : N_high元素中有所不同。因此,只需计算integrand_exp_high,并将integrand_exp_low设置为integrand_exp_high的第一个N_low元素。
然后,精细方法使用原始实现(使用实际的integral()),但从粗步骤的更新初始估计开始。
这里的整个目标是尝试将所需的迭代总数从大约6次减少到少于2次。也许您甚至会发现trapz方法已经提供了足够的准确性,因此没有必要执行整个精细的步骤。
矢量化
上面概述的粗步骤中的矩形方法很容易矢量化:
% (uses R2016b implicit expansion rules)
Elo = linspace(0, E_low, numel(S_low));
integrand_exp_low = exp(x(:,1)./Elo.^3 + x(:,2).*fKN(Elo));
Ehi = linspace(0, E_high, numel(S_high));
integrand_exp_high = exp(x(:,1)./Ehi.^3 + x(:,2).*fKN(Ehi));
F = [I_high_vector - (S_high * integrand_exp_high) * (Ehi(2) - Ehi(1))
I_low_vector - (S_low * integrand_exp_low ) * (Elo(2) - Elo(1))];trapz也可以处理矩阵;它将在矩阵中的每一列上进行集成。
然后使用x0 = [x01; x02; ...; x0N]调用x0 = [x01; x02; ...; x0N],然后fsolve将收敛到[x1; x2; ...; xN],其中N是体素数,每个x0为1×2 ([x(1) x(2)]),所以x0为N×2。
parfor应该能够很容易地将所有这些都分割到池中的所有员工上。
同样,精细方法的矢量化也是可能的;只需将'ArrayValued'选项用于integral(),如下所示:
F = [I_high_vector - integral(@(E) S_high(E) .* exp(x(:,1)./E.^3 + x(:,2).*fKN(E)),...
0, E_high,...
'ArrayValued', true);
I_low_vector - integral(@(E) S_low(E) .* exp(x(:,1)./E.^3 + x(:,2).*fKN(E)),...
0, E_low,...
'ArrayValued', true);
];雅可比
利用函数的导数是相当容易的。这里是导数w.r.t.x_1和这里 w.r.t.x_2。你的雅可比矩阵必须是2×2矩阵
J = [dF(1)/dx(1) dF(1)/dx(2)
dF(2)/dx(1) dF(2)/dx(2)]; 别忘了前面的负号(F = I_hi/lo - g(x)→dF/dx = -dg/dx)
使用上述一种或两种方法,您可以实现一个函数来计算雅可比矩阵并通过'SpecifyObjectiveGradient'选项() )将其传递给fsolve。'CheckGradients'选项在那里会派上用场。
由于fsolve通常会花费绝大部分时间通过有限差分计算雅可比,手动计算它的值通常会极大地加快算法的速度。
会更快,因为
fsolve不需要做额外的函数计算来完成有限的差异- 由于雅可比精度的提高,收敛速度会提高。
特别是如果您像上面这样使用矩形方法或trapz,您可以重用已经为函数值本身完成的许多计算,这意味着,甚至更快。
Stack Overflow用户
发布于 2017-01-18 16:15:41
罗迪的答案是正确的。为雅可比人提供食物是唯一最大的因素。特别是矢量化的版本,在速度上有三个数量级的差异,与雅可比提供和不。
我很难在网上找到关于这一主题的信息,所以我将在这里详细说明,以供将来参考:它是可以向量独立的并行方程与fsolve(),取得了很大的成就。
我还做了一些内联的工作,fsolve()。在提供Jacobian和更聪明的方程式之后,我的代码的串行版本主要是以每个体素1*10^-3s为代价。在这一点上,函数内部的大部分时间都用于传递选项-struct和创建错误消息,这些错误消息从未被发送过,并为优化函数中的其他优化函数添加了大量未使用的内容(levenberg-marquardt给我)。我成功地销毁了函数some和它调用的一些函数,将时间减少到机器上的每个体素1*10^-4s。因此,如果您被串行实现困住了,例如,由于必须依赖于前面的结果,那么很有可能内联fsolve()并取得良好的结果。
在我的例子中,矢量化版本提供了最好的结果,每个体素有~5*10^-5s。
https://stackoverflow.com/questions/41591639
复制相似问题

