使用当前实际国产总值/GDP数据的Python
我一直在使用statsmodel.tsa.MarkovAutoregressio复制哈密顿在1989年发表的马尔可夫切换模型。如果使用Hamilton数据(1982年美元的实际国产总值),我可以得到与代码示例/文件显示的结果相同的结果。然而,当我使用当前可用的实际国产总值或GDP数据(以2009年美元为单位)并以它们的日志差(季度)作为输入时,该模型并没有给出令人满意的结果。
我绘制了汉密尔顿国民生产总值的对数差额,这是从目前可用的实际国民生产总值中得出的。他们非常接近,差别很小。
有人能告诉我为什么会这样吗?这与当前国产总值数据的季节性调整有何关系?如果是的话,是否有办法对付呢?
使用现有国产总值的结果
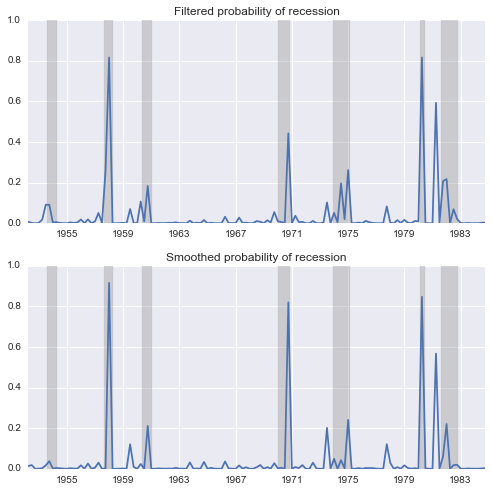
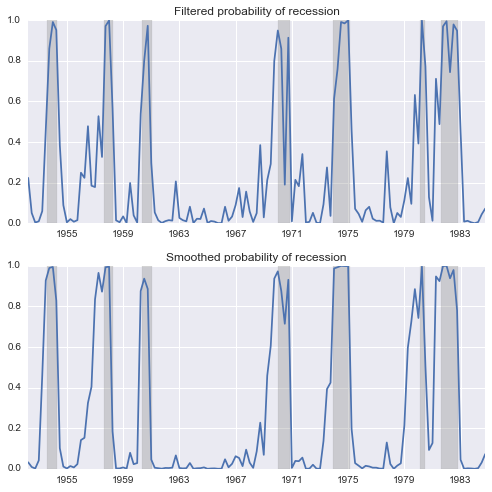
使用纸张提供的国产总值的结果
回答 1
Stack Overflow用户
发布于 2017-04-03 00:38:56
你写:
该模型没有给出满意的结果。
但你的意思是,模型并没有给出你期望/想要的结果。也就是说,您希望模型选择NBER标记为“衰退”的周期,而马尔可夫切换模型只是寻找数据最大似然函数的参数。
(文章的其余部分显示了这个木星笔记本的结果:http://nbviewer.jupyter.org/gist/ChadFulton/a5d24d32ba3b7b2e381e43a232342f1f)
(我还将注意到,我使用E视图对这些结果进行了二次检查,它与Statsmodels的输出几乎完全一致)。
原始数据集是实际国民生产总值的增长率(对数差* 100);此处显示了汉密尔顿数据集与美联储经济数据库中的数据,灰色条表示NBER日期的衰退:
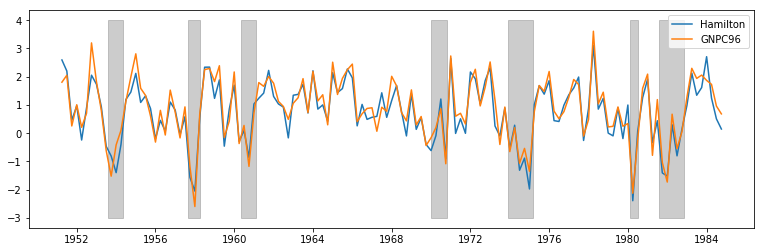
在这种情况下,模型是关于实际国产总值增长率的AR(4),具有一个特定于制度的截距;该模型允许两个机制。这种观点认为,“衰退”应对应于低(或负)平均增长率,而扩张应对应于较高的平均增长率。
模型1: Hamilton数据集:参数的最大似然估计
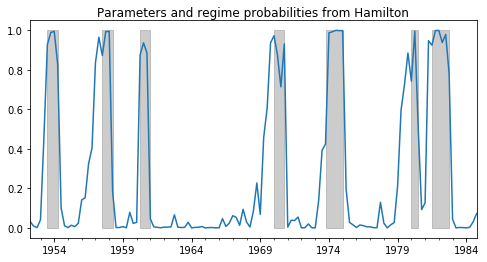
从哈密顿(1989)数据集的模型中,我们得到了以下估计参数:
Markov Switching Model Results
================================================================================
Dep. Variable: Hamilton No. Observations: 131
Model: MarkovAutoregression Log Likelihood -181.263
Date: Sun, 02 Apr 2017 AIC 380.527
Time: 19:52:31 BIC 406.404
Sample: 04-01-1951 HQIC 391.042
- 10-01-1984
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.3588 0.265 -1.356 0.175 -0.877 0.160
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.1635 0.075 15.614 0.000 1.017 1.310
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 0.5914 0.103 5.761 0.000 0.390 0.793
ar.L1 0.0135 0.120 0.112 0.911 -0.222 0.249
ar.L2 -0.0575 0.138 -0.418 0.676 -0.327 0.212
ar.L3 -0.2470 0.107 -2.310 0.021 -0.457 -0.037
ar.L4 -0.2129 0.111 -1.926 0.054 -0.430 0.004
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.7547 0.097 7.819 0.000 0.565 0.944
p[1->0] 0.0959 0.038 2.542 0.011 0.022 0.170
==============================================================================在0状态下运行的概率的时间序列(这里对应于负增长率,即衰退)如下:
模型2:更新的数据集:参数的最大似然估计
现在,正如您所看到的,我们可以使用“更新”数据集(看起来很像原始数据集)来拟合模型,以获得以下参数和系统概率:
Markov Switching Model Results
================================================================================
Dep. Variable: GNPC96 No. Observations: 131
Model: MarkovAutoregression Log Likelihood -188.002
Date: Sun, 02 Apr 2017 AIC 394.005
Time: 20:00:58 BIC 419.882
Sample: 04-01-1951 HQIC 404.520
- 10-01-1984
Covariance Type: approx
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -1.2475 3.470 -0.359 0.719 -8.049 5.554
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.9364 0.453 2.066 0.039 0.048 1.825
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 0.8509 0.561 1.516 0.130 -0.249 1.951
ar.L1 0.3437 0.189 1.821 0.069 -0.026 0.714
ar.L2 0.0919 0.143 0.645 0.519 -0.187 0.371
ar.L3 -0.0846 0.251 -0.337 0.736 -0.577 0.408
ar.L4 -0.1727 0.258 -0.669 0.503 -0.678 0.333
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.0002 1.705 0.000 1.000 -3.341 3.341
p[1->0] 0.0397 0.186 0.213 0.831 -0.326 0.405
==============================================================================
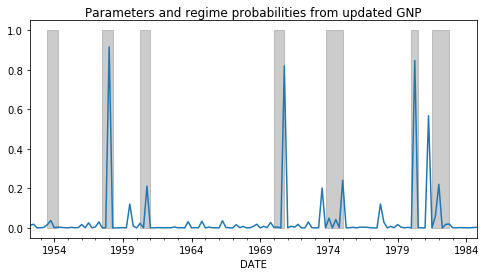
要了解这个模型正在做什么,请看一下这两个政权的拦截。在Hamilton模型中,“低”系统的截获值为-0.35,而根据更新的数据,“低”系统的截获值为-1.25。
这告诉我们,在更新的数据集中,该模型通过选择“低”机制来进行更深层次的衰退,从而“更好地”拟合数据(就更高的可能性而言)。特别是,回顾国民生产总值数据系列,很明显,它是在利用“低”制度来适应50年代末和80年代初非常低的增长。
相比之下,汉密尔顿模型的拟合参数允许“低”制度适应“中等低”增长率,涵盖范围更广的衰退。
我们不能用日志似然值来比较这两个模型的结果,因为它们使用的是不同的数据集。不过,我们可以尝试的一件事是,在更新的国产总值数据中使用汉密尔顿数据集中的拟合参数。这样做,我们得到了以下结果:
模型3:使用Hamilton数据集上估计的参数更新数据集
Markov Switching Model Results
================================================================================
Dep. Variable: GNPC96 No. Observations: 131
Model: MarkovAutoregression Log Likelihood -191.807
Date: Sun, 02 Apr 2017 AIC 401.614
Time: 19:52:52 BIC 427.491
Sample: 04-01-1951 HQIC 412.129
- 10-01-1984
Covariance Type: opg
Regime 0 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.3588 0.185 -1.939 0.053 -0.722 0.004
Regime 1 parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.1635 0.083 13.967 0.000 1.000 1.327
Non-switching parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sigma2 0.5914 0.090 6.604 0.000 0.416 0.767
ar.L1 0.0135 0.100 0.134 0.893 -0.183 0.210
ar.L2 -0.0575 0.088 -0.651 0.515 -0.231 0.116
ar.L3 -0.2470 0.104 -2.384 0.017 -0.450 -0.044
ar.L4 -0.2129 0.084 -2.524 0.012 -0.378 -0.048
Regime transition parameters
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
p[0->0] 0.7547 0.100 7.563 0.000 0.559 0.950
p[1->0] 0.0959 0.051 1.872 0.061 -0.005 0.196
==============================================================================
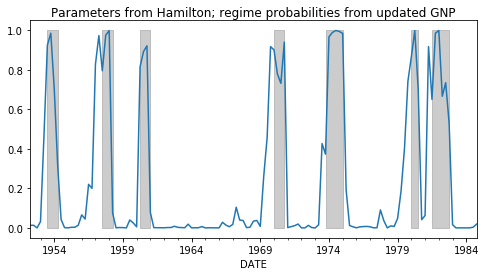
这看起来更像您所期望/想要的,这是因为正如我前面提到的,0.35的“低”体制拦截使得“低”机制非常适合于样本中更多的时间段。但是请注意,这里的对数可能性是-191.8,而在模型2中,log-可能性是-188.0.
因此,即使这个模型看起来更像您想要的,它也不适合数据。
(请再次注意,您不能将这些日志概率与Model 1中的-181.3进行比较,因为它使用的是不同的数据集)。
https://stackoverflow.com/questions/42796743
复制相似问题

