matlab / python中的局部直方图均衡
我是matlab中的新手。我想编写本地直方图均衡化的代码。我已经为全局直方图均衡编写了代码,我知道局部均衡意味着对图像的每个部分进行均衡,但我的问题是我应该如何选择图像的这一部分?例如,我是否应该对与其他像素分离的每100个像素进行均衡化?换句话说,我如何将图像分割成某些部分,然后对每个部分进行均衡?
回答 2
Stack Overflow用户
发布于 2017-03-25 07:39:18
最天真的方法是将图像分割成不重叠的块,在该块上执行全局直方图代码并将其保存到输出中。假设您将这些不重叠块的行和列定义为变量rows和cols。在您的例子中,假设是100x100,所以是rows = 100; cols = 100;。您可以简单地遍历每个不重叠的块,进行直方图均衡化,然后将其设置为输出中的相同位置。
如下所示,假设您的图像存储在im中
rows = 100;
cols = 100;
out = zeros(size(im)); % Declare output variable
for ii = 1 : rows : size(im, 1)
for jj = 1 : cols : size(im, 2)
% Get the block
row_begin = ii;
row_end = min(size(im, 1), ii + rows);
col_begin = jj;
col_end = min(size(im, 2), jj + cols);
blk = im(row_begin : row_end, col_begin : col_end, :);
% Perform histogram equalization with the block stored in blk
% ...
% Assume the output of this is stored in O
out(row_begin : row_end, col_begin : col_end, :) = O;
end
end请注意存储不重叠块的变量blk的复杂性。我们让开头的行和列只是循环计数器ii和jj,但是结尾的行和列必须确保它被图像的维数所限制。这就是为什么min电话在那里。否则,结束行和列只是由相应维度中的块的大小添加的开始行和列。还请注意,我已经使用:索引到第三维空间,以防你有一个彩色图像。灰度不应影响此代码。在将输出存储在输出映像中时,最终需要使用相同的索引。注意,我假设它存储在变量O中,这是您定制的直方图均衡器函数的输出。
输出out将包含本地直方图均衡化图像。请注意,理论上您可以使用图像处理工具箱中的blockproc (如果有)在一行中完成此操作。这将处理图像中的不同块,并对其应用一些功能。假设您的直方图均衡器函数称为hsteq,您只需这样做:
rows = 100; cols = 100;
out = blockproc(im, [rows, cols], @(s) hsteq(s.data));第一个输入是要处理的图像,第二个输入定义块大小,最后一个元素是要应用于每个块的函数。请注意,blockproc为您的函数提供了一个自定义的结构,因此重要的是提取结构中的data字段。这将产生与上面循环代码相同的输出。
Stack Overflow用户
发布于 2022-06-15 23:49:25
我们可以使用基于块的局部(自适应)直方图均衡化来实现AHE (如另一个答案中所建议的),但在这种情况下,我们需要实现类似双线性插值的技术,以防止窗口边缘的对比度突然发生变化,例如,观察下面与python实现相同的均衡化输出(这里为该窗口使用了一个50x50窗口):
def AHE(im, tile_x=8, tile_y=8):
h, w = im.shape
out = np.zeros(im.shape) # Declare output variable
for i in range(0, h, tile_x):
for j in range(0, w, tile_y):
# Get the block
blk = im[i: min(i + tile_x, h), j: min(j + tile_y, w)]
probs = get_distr(blk)
out[i: min(i + tile_x, h), j: min(j + tile_y, w)] = CHE(blk, probs)
return out
def CHE(im, probs):
T = np.array(list(map(int, 255*np.cumsum(probs))))
return T[im]
def get_distr(im):
hist, _ = np.histogram(im.flatten(),256,[0,256])
return hist / hist.sum()
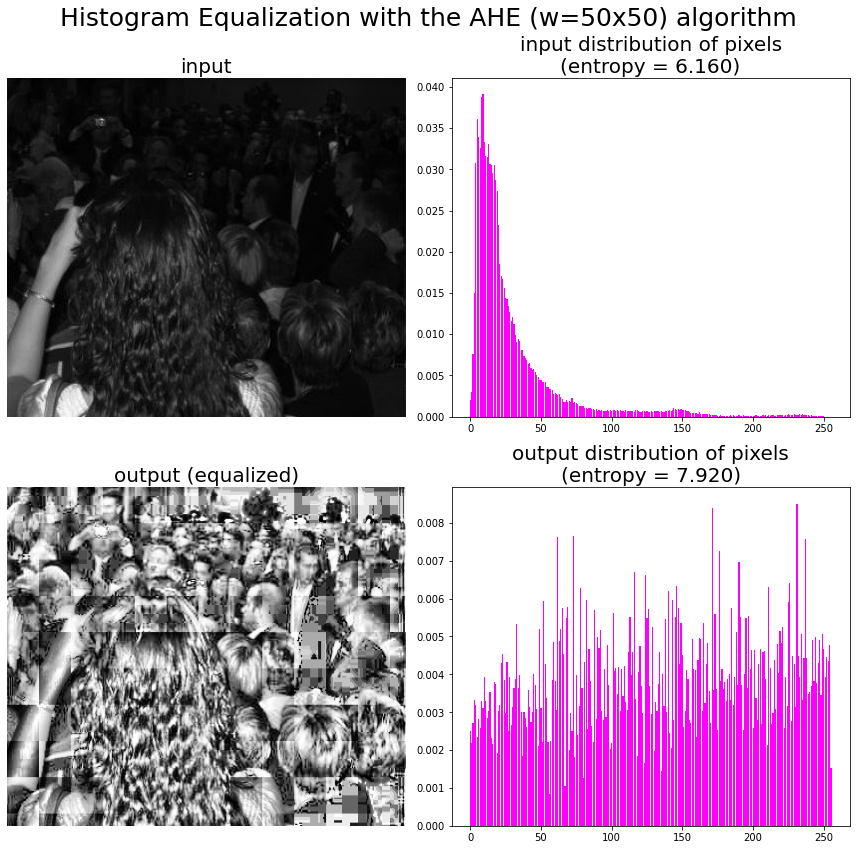
我们可以从本论文实现AHE算法

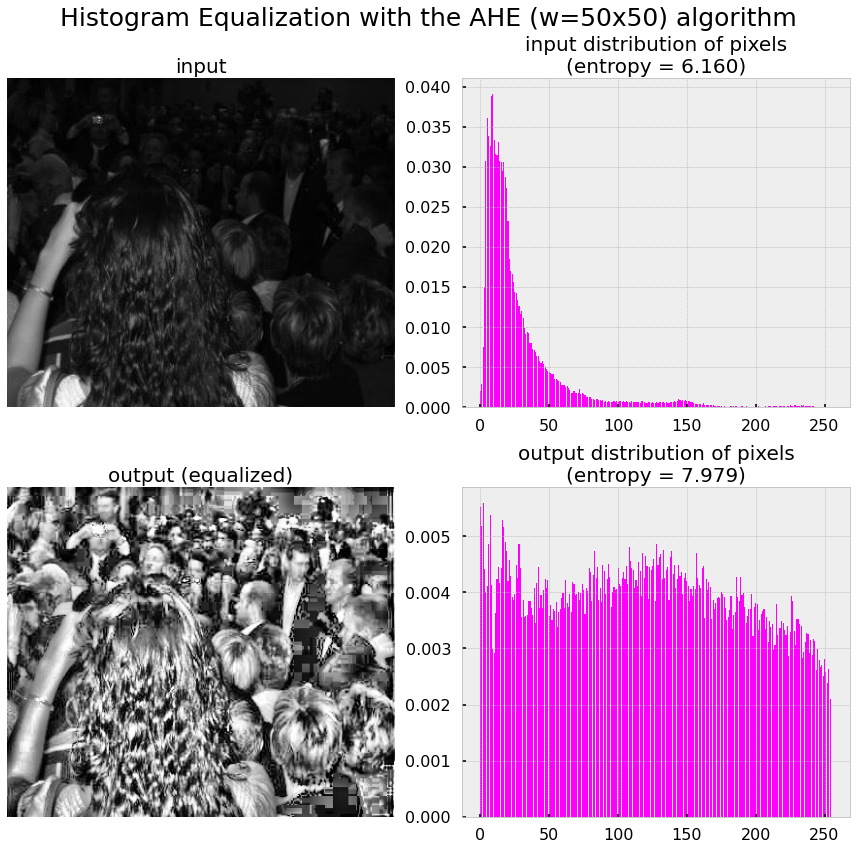
算法的实现产生了更好的结果(没有边界伪影):
https://stackoverflow.com/questions/43013492
复制相似问题

