如何在matlab中用分段线性函数拟合具有一定约束条件的边坡数据
如何在matlab中用分段线性函数拟合具有一定约束条件的边坡数据
提问于 2017-04-25 06:05:29
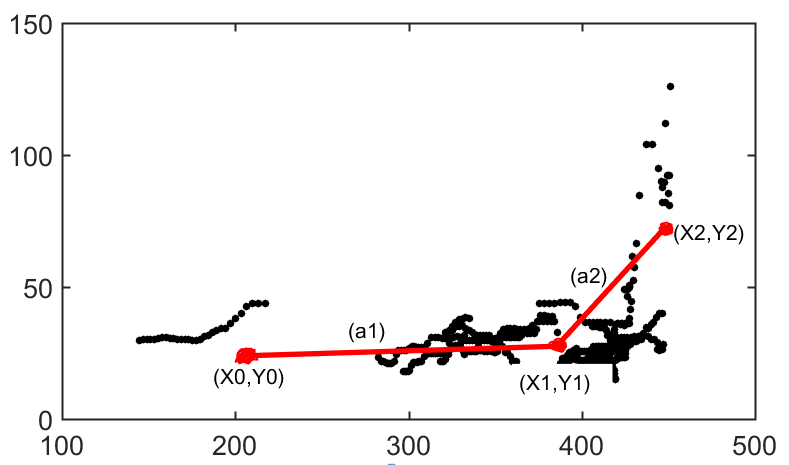
我试图为我的(xdata, ydata)数据拟合一个分段线性方程。我不得不面对挑战,第一个问题是如何以函数句柄的形式转换方程,第二个问题是如何在斜率上设置一个约束,例如,a2>a1、a2>0和a1>0。
xdata = 5:0.2:40;
ydata = max(18,xdata) + 0.5*randn(size(xdata));
a1 = (y1-y0)/(x1-x0); a2 = (y2-y1)/(x2-x1);
if x < x1;
f(x) = y0 + a1*(x-x0);
else
f(x) = y0 + a1*(x1-x0) + a2*(x-x1);
end
FU = matlabFunction(f)
x0 = 5; y0 = 16;
x = lsqcurvefit(FU,[x0,y0],xdata,ydata)
回答 1
Stack Overflow用户
回答已采纳
发布于 2017-04-25 08:26:37
创建分段函数的关键是用向量化的if替换>条件。通过在某些数组y = x > 1上调用x,输出y将是一个与x大小相同的数组,如果x中的对应元素大于1,则为逻辑True,否则为False。例如
>> x = [1, 2, 4; 3, 1, 2];
>> y = x > 2
y =
2×3 logical array
0 0 1
1 0 0您可以利用它创建一个分段线性函数,如下所示:
>> fun = @(theta, xdata) theta(1) + ...
(xdata<=theta(2)) .* theta(3) .* xdata + ...
(xdata>theta(2)) .* (theta(3) * theta(2) + ...
theta(4) .* (xdata-theta(2)))参数向量theta是四维的:第一个元素是从零开始的常数偏移,第二个元素是拐角点,第三个和第四个元素是两个斜率。
通过将theta(3).*xdata与xdata<=theta(2)的结果相乘,可以得到xdata中小于theta(2)的每个点的theta(3).*xdata,以及所有其他点的0。
然后,调用lsqcurvefit非常简单
>> theta = lsqcurvefit(fun, [0; 15; 0; 1], xdata, ydata)
theta =
18.3793
17.9639
-0.0230
0.9943
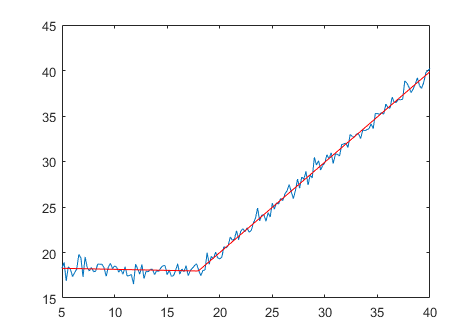
lsqcurvefit函数还允许您为要估计的变量指定一个下限lb和一个上限ub。对于不想指定绑定的变量,可以使用例如inf作为绑定。为了确保您的a1和a2 (即theta(3)和theta(4) )是正的,我们可以指定下界为[-inf, -inf, 0, 0]。
但是,lsqcurvefit函数不允许您添加约束a2 > a1 (或任何线性不等式约束)。在示例数据中,这个约束可能甚至不是必需的,因为从数据中可以看出这一点。否则,可能的解决方案是将a2替换为a1 + da,并为da使用0的下限。这确保了a2 >= a1。
>> fun = @(theta, xdata) theta(1) + ...
(xdata<=theta(2)) .* theta(3) .* xdata + ...
(xdata>theta(2)) .* (theta(3) * theta(2) + ...
(theta(3)+theta(4)) .* (xdata-theta(2)))
>> theta = lsqcurvefit(fun, [0; 15; 0; 1], xdata, ydata, [-Inf, -Inf, 0, 0], [])
theta =
18.1162
18.1159
0.0000
0.9944页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/43602835
复制相关文章
相似问题

