问具有n个任务和m台机器的作业调度

EN

问题描述：

我有n优先约束作业和m独立机器。每个作业都有一个分配给它的成本c (在1时间单元中完成任务所需的机器数量)。完成一项任务需要1时间单位，只有将c机器分配给它才能完成作业(作业是原子的，不可能完成一半的作业)。

因此，简而言之，存在n作业及其优先级约束、m机器和截止日期d (一定数量的时间单位)。

我的目标：

我想检查是否有可能将作业分配给机器，以便所有的作业都在d时间单位内完成。如果这是可能的，那么我想打印一个为每个作业分配一个时间单元的计划(处理作业的时间单位，参见下面的示例)。

示例：

n = 5; // number of jobs
m = 6; // number of machines
d = 4; // deadline (number of time units in which the jobs need to be finished)

Precedences: (read "Job(x,y)<--Job(q,p)" as "job x with cost y needs to be
              finished before job q with cost p can be started")
Job(3,1)<--Job(2,3)<--Job(1,4)
Job(5,3)<--Job(4,3)
Job(6,1)

 The solution: in this case it's possible to assign jobs to machines such that each job
finishes in <=d time units. 
A possible schedule is 1 2 3 3 4 1.

(read schedule as "job 1 and job 6 are done in the first time unit, job 2
is done during the second time unit, jobs 3 and 4 during the third time unit, 
job 5 during the fourth time unit")

当前的方法：(第二次尝试感谢@Ole V.V.的反例)

我想做一个回溯方法(最好的方法，我可以想出)。目前，我执行它有困难。

我想保存工作和他们的先例。然后，我确定了一个集合A，它包含在当前时间单元中可以解决的所有作业。然后，我找到一个集合B(它包含我在这个时间单元中考虑解决的所有作业集)，其中包含A的所有子集，这些子集在有限的机器m中是可解决的，这样就不能向每个子集添加其他作业(通过将作业添加到其中一个子集中，该子集中所有作业的成本都超过'm')。然后我重复这个过程，但是没有已解决的作业(A\ B )，我对B中的每个子集执行递归调用。当传递的剩馀作业集(A\B)为空(所有作业都已完成)时，我停止。此时，如果递归的深度为<= d (如果满足最后期限)，则返回找到的时间表。

这种方法的例子由@Ole V.V.提供：

​

​

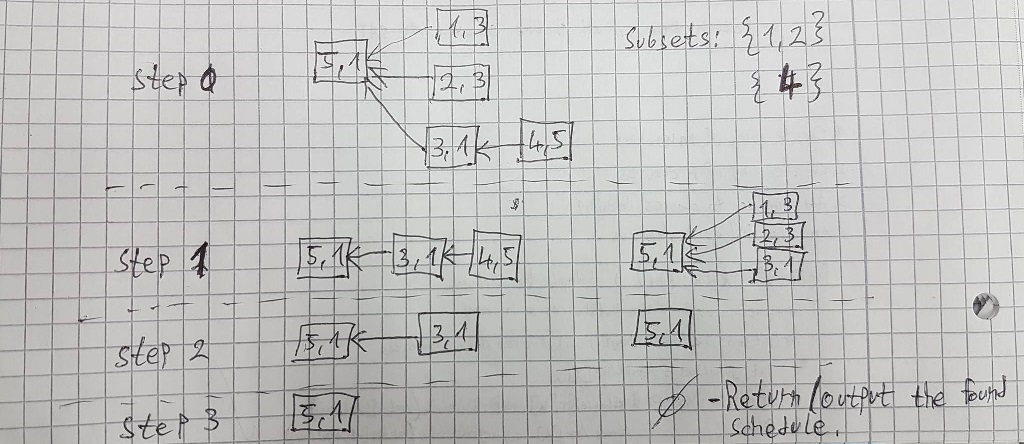
步骤引用递归的深度，框引用作业(第一个数字是作业ID，第二个是时间单位的成本)。在步骤0中，我显式地写出了子集(在这一步中我考虑解决的一组作业)。

现在我的问题是储存作业及其先例，找出可以在现时时间单位(A组)内解决的工作，找出我在现时时间单位(B组)内考虑解决的工作子集，并把这些工作组合成一个递归函数，最终输出已找到的时间表，或在没有时间单位(集合B)的情况下，输出“未找到的时间表”。