拟合多模态分布
拟合多模态分布
提问于 2017-07-05 19:48:39
假设我们有两个正态分布的线性组合。我想人们会把这个结果称为多峰分布。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
ls = np.linspace(0, 60, 1000)
distribution = norm.pdf(ls, 0, 5) + norm.pdf(ls, 20, 10)
distribution = (distribution * 1000).astype(int)
distribution = distribution/distribution.sum()
plt.plot(ls, distribution)
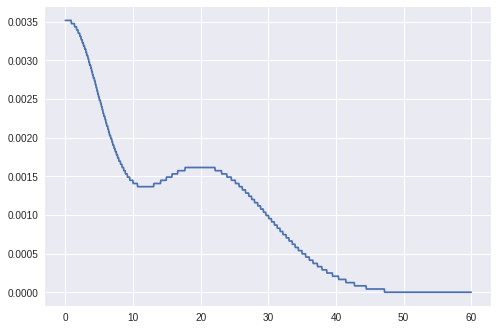
正如您所看到的,我们有两个正态分布的线性组合,参数为(mu1 = 0, s1 = 5)和(mu2 = 20, s2 = 10)。当然,我们通常事先不知道这些参数。
我想知道如何估计或拟合这些参数(毛里求斯和西格玛)。我相信有一些方法可以让我做到这一点,但我还没有找到任何方法。
回答 2
Stack Overflow用户
回答已采纳
发布于 2017-07-05 20:39:33
您描述的问题是高斯混合模型的特例。为了能够估计这些参数,您需要一些样本。如果你没有样本,但你得到了曲线,你可以根据曲线产生一些样本。然后可以使用期望最大化算法来估计参数。Scikit--学习有一种方法可以让你做到这一点:sklearn.mixture.GaussianMixture。您只需提供您的样本、组件数量(n_components) (在您的情况下为2)和协方差类型(在您的情况下为full ),因为您之前对协方差矩阵没有任何假设。
Stack Overflow用户
发布于 2017-07-05 20:40:38
您可能需要使用期望最大化算法。
这是一种迭代方法,允许您拟合混合组分的模型。在scikit中有一个非常方便的实现--学习:GaussianMixture
我发现很难知道如何构造数据以使该算法工作,所以我为您设置了一个示例:https://nbviewer.jupyter.org/gist/lhk/e566e2d6b67992eca062f9d96e2a14a2
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/44934808
复制相关文章
相似问题

