模拟离散房间中的降压
我正在试图建立一个自上而下的太空飞船游戏,其中有可摧毁的部分。我需要模拟在船体破裂情况下的减压过程。
我有一张平铺的地图,里面有房间分区代码设置:
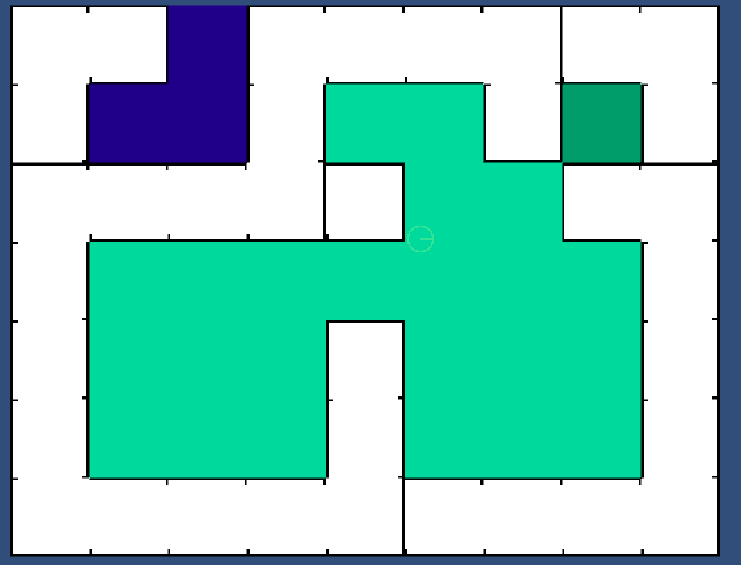
我想要做的是建立一个向量场来决定空气离开减压空间的方式。因此,如果你打破了连接真空和房间的瓷砖(毗邻紫色和绿色的房间),你最终会得到这样的矢量地图:
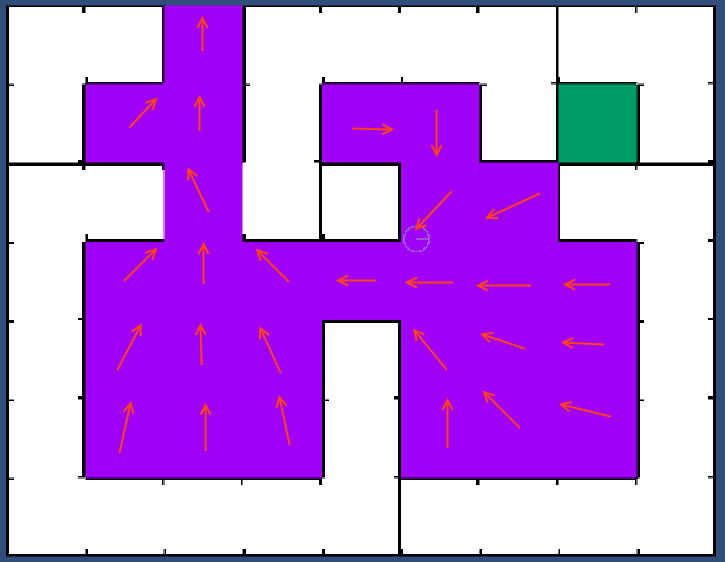
我的想法是实现某种标量场(类似于势场)来帮助确定气流(基本上用欧氏距离填充网格(考虑障碍)到一个已知的零势点,然后考虑到当前瓷砖所具有的所有潜在值较低的相邻瓦片,计算向量:
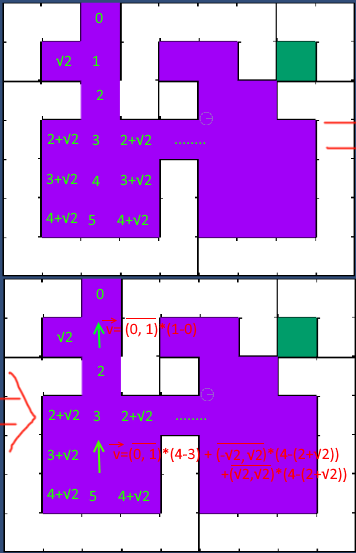
但是,这种方法存在一个缺陷,即在某一点上对物体施加的力的大小并没有真正考虑气流瓶颈和距离,所以在真空瓦旁边的瓷砖和房间的另一端的力应该是相同的。
是否有更好的方法来模拟这种行为,或者对算法进行修改,我认为这或多或少会考虑到距离和瓶颈?
回答 1
Stack Overflow用户
发布于 2017-07-27 07:28:32
算法升级从评论中收集到的思想:
(...)在这种情况下,你想要一种真实的“力”感觉,那么它不应该仅仅基于距离,而是,就像你说的,气流。您需要在某种程度上估计它,并注意它的行为类似于电子产品中的Kirchoff规则。假设这个洞很小,那么每秒吸进的空气量很小。第一个最近的瓷砖必须覆盖它,他们失去X空气每秒。它们周围的瓷砖也必须将其吸收--它们每秒总共会失去X空气。和他们的邻居..。诸若此类。它的工作原理就像Dijkstra距离但是倒数。
例如:假设没有墙,从点每秒16秒开始,指向地面上的洞,周围的8个瓷砖将得到2/秒的指向零点瓷砖。下一层周围的12个瓷砖将得到大约1.33秒,以此类推。现在,改变这一点,即(1)考虑不同的初始孔尺寸,(2)各种大的无通障碍(3)由于小通道的气流限制-这表现为新的起点。
另一个例子(从图中):值为零的瓷砖的值是,比如说1000单位/秒,低于这个值的是500/s,下一个也是1000/s,与之相连的三个单位都是333/s。
在此基础上,我们可以根据这个标量值的差值来确定向量的系数,因为它考虑了障碍和距离,所以它或多或少地是实际工作的。
关于上面的第(3)点,想象一下,与其只有-100%的传球和不-0%的墙,你还有中间的选择。不只是一条走廊和一堵墙,你也可以有破碎的窗户,30%的通风口。例如,在地图上有距离的地方,有一个初始孔,它能产生1000秒的流量。然而,在距离2,有一个小的空气通风口或一个破碎的窗口与30%的气流改性剂。这意味着它将限制从传入(2x500=1000)到0.3x(2x500)=300/秒的数量,这将进一步流到下一个区域。这将允许你以不同的速度减压舱室,所以前几块瓷砖很快就会失去所有的空气,而甲板的其他部分将需要更多的时间(除非在第2点的30%的修改器窗口完全断裂,等等)。
https://stackoverflow.com/questions/45343472
复制相似问题

