用R进行不匹配F检验
我学会了如何使用R来进行F-检验,因为回归模型缺乏拟合,其中$H_0$:“回归模型中并不缺少拟合”。
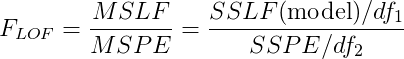
其中,df_1是SSLF (缺少拟合平方和)的自由度,df_2是SSPE (纯误差平方和)的自由度。
在R中,F检验(例如对于有两个预测因子的模型)可以用以下方法计算。
anova(lm(y~x1+x2), lm(y~factor(x1)*factor(x2)))
示例输出:
Model 1: y ~ x1 + x2
Model 2: y ~ factor(x1) * factor(x2)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 19 18.122
2 11 12.456 8 5.6658 0.6254 0.7419F-统计量: 0.6254,p值为0.7419.
由于p-值大于0.0 5,所以我们不拒绝$H_0$,即不缺少fit。因此,该模型是充分的。
我想知道的是,为什么使用2模型,为什么使用factor(x1)*factor(x2)命令?显然,来自Model 2的12.456是神奇地为Model 1而设的SSPE。
为什么?
回答 1
Stack Overflow用户
发布于 2017-07-28 09:14:21
您正在测试一个具有交互作用的模型是否会改善模型的适合性。
模型1对应于x1和x2的加性效应。
一种“检查”一个模型的复杂性是否足够的方法(在你的例子中,带有加性效应的多元回归对你的数据是否有意义)是将提议的模型与一个更灵活/复杂的模型进行比较。
您的模型2具有这个更灵活的模型的作用。首先对预测器进行分类(使用factor(x1)和factor(x2)),然后用factor(x1)*factor(x2)构造它们之间的交互关系。交互模型包括作为特例的加性模型(即,模型1嵌套在模型2中),并且有几个额外的参数来提供可能更适合数据的参数。
在来自anova的输出中,您可以看到两个模型之间的参数数量不同。模型2有8个额外的参数以允许更好的拟合,但是由于p值不是显着性的,所以您会得出结论,模型2(基于附加的8个参数具有额外的灵活性)实际上并不能提供对数据的更好的匹配。因此,与模型2相比,相加模型为数据提供了足够合适的匹配。
请注意,上面使用x1和x2的类别(因素)的技巧只有在x1和x2的唯一值数量较低时才能真正发挥作用。如果x1和x2是数字的,并且每个个体都有自己的值,那么模型2并不那么有用,因为您最终得到的参数数量与您的观察值相同。在这种情况下,会使用更多的临时修改,例如绑定变量。
https://stackoverflow.com/questions/45364277
复制相似问题

