hermitian矩阵ARPACK的奇异性质
hermitian矩阵ARPACK的奇异性质
提问于 2017-08-30 15:54:56
我想得到一些厄米矩阵的基态能量(见下面代码中这个矩阵的定义),并用矩阵参数“相位”来绘制它。
import scipy.sparse as sparse
import scipy
import numpy
import numpy as np
import math
from scipy.special import binom
import cmath
import sympy
import matplotlib.pyplot as plt
import pylab
from copy import *
from numpy import linalg as LA
M=5#DIMENSION OF THE MATRIX
def tunneling(phase):#HAMILTONIAN MATRIX
Matrix_hop = [[0 for x in range(M)] for y in range(M)]
for i in range(M):
if i+1==M:
Matrix_hop[i][0] = -1.0
Matrix_hop[i][i-1] = -1.0
else:
Matrix_hop[i][i+1] = -1.0
Matrix_hop[i][i-1] = -1.0
Matrix_hop[0][M-1]=-1.0*cmath.exp(1j*phase)
Matrix_hop[M-1][0]=-1.0*cmath.exp(-1j*phase)
return Matrix_hop
def eigen_system(H):
values, vectors = sparse.linalg.eigs(H,2,which='SR') #ARPACK!!
energy_ground = values[0]
return vectors[:,0], energy_ground
init = 0.0
points = 1000
final_value = 2*math.pi
steep = (final_value-init)/points
list_values_phase = np.arange(init,final_value,steep)
f1 = open("ground_state_energy.dat", "w")
for i in list_values_phase:
phase = i
f1.write(str(phase)+" ")
H = np.asarray(tunneling(i))
f1.write(str(np.real(eigen_system(H)[1]))+" ")
f1.write("\n")
f1.close()
datalist = pylab.loadtxt("ground_state_energy.dat")
pylab.plot( datalist[:,0], datalist[:,1],label="ground state" )
pylab.legend()
pylab.xlabel("phase")
pylab.ylabel("Energy")
pylab.show()我在Python中对hermitian矩阵使用了ARPACK,这是使用sparse.linalg.eigs完成的。问题是,如下图所示,基态能量没有正确计算,有很多峰值,这意味着基态找不到。实际上,对于这个山峰,ARPACK没有找到基态,而是获得了第一个激发状态。
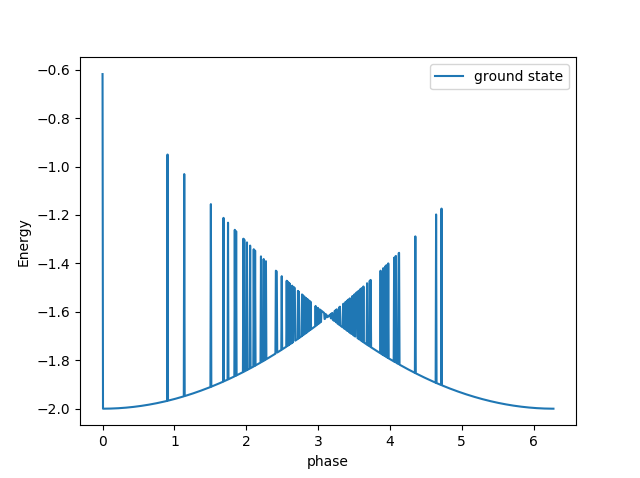
这是一个非常奇怪的问题,因为我使用的这个矩阵(来自量子力学)可以用数学方法来解析,用Python中的ARPACK也不能工作。有人知道为什么会发生这种情况,如何解决??谢谢
我正在使用的最后一个versión的枕0.19.1
回答 1
Stack Overflow用户
回答已采纳
发布于 2017-08-30 17:43:27
在这个职能中
def eigen_system(H):
values, vectors = sparse.linalg.eigs(H,2,which='SR') #ARPACK!!
energy_ground = values[0]
return vectors[:,0], energy_ground找到前两个特征值,然后取第一个特征值。函数eigs不能保证它找到的特征值是有序的,有时第一个特征值不是最小的。
与其找到两个最小的,为什么不直接找到最小的?
values, vectors = sparse.linalg.eigs(H, 1, which='SR') # ARPACK!!当我做出改变的时候,我得到了这样的情节:
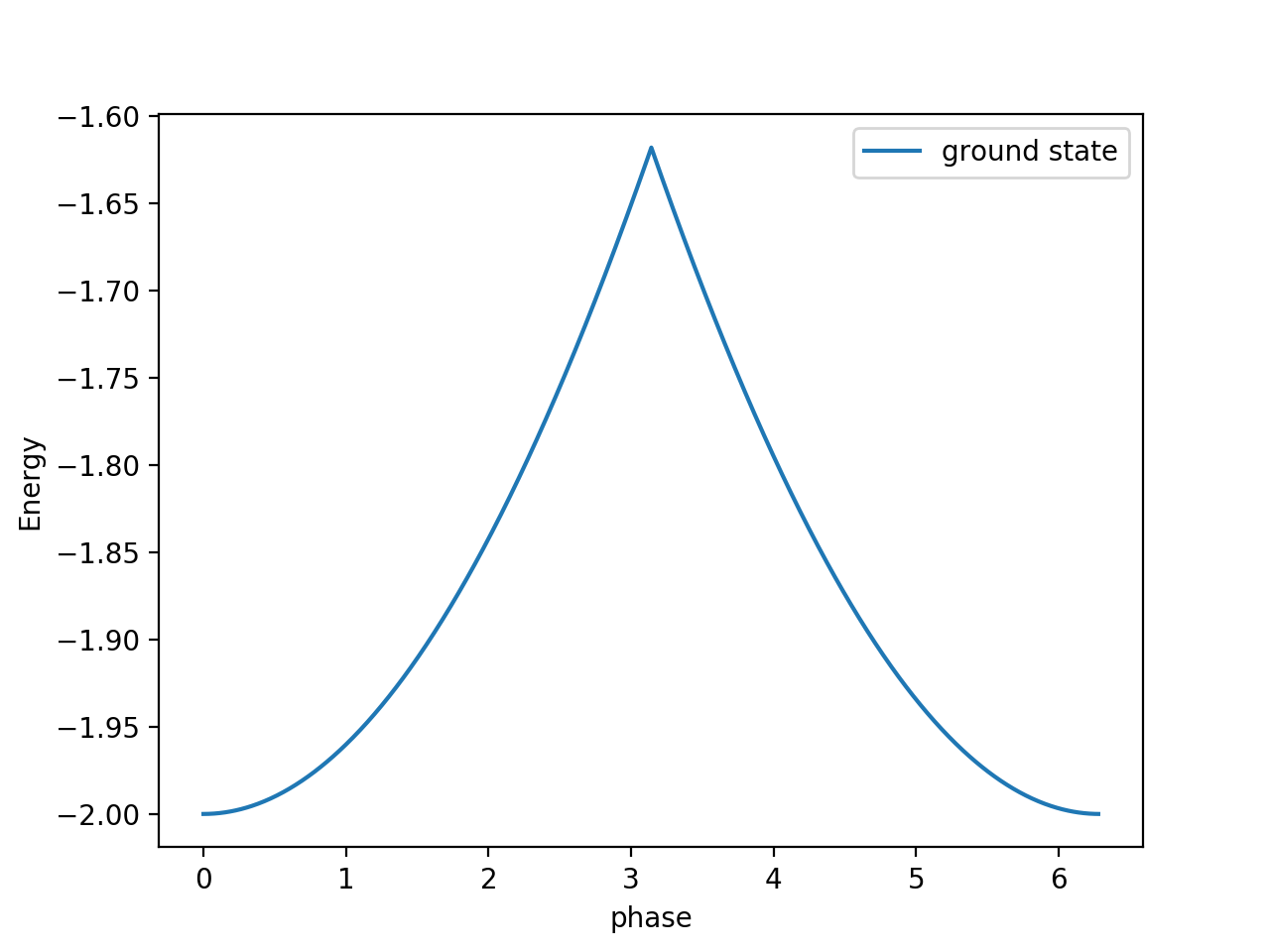
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/45964891
复制相关文章
相似问题

