查找与大数据集中每个点最近的线,可能使用shapely和rtree
我有一张简化的城市地图,其中有街道作为线串,地址作为点。我需要找到从每个点到任何一条街道的最近的路径。我有一个执行此操作的脚本,但是它在多项式时间内运行,因为它已经嵌套了for循环。对于15万行(shapely LineString)和10000点(shapely Point),它需要10个小时完成8 GB的Ram计算机。
该函数如下所示(很抱歉没有使它完全可复制):
import pandas as pd
import shapely
from shapely import Point, LineString
def connect_nodes_to_closest_edges(edges_df , nodes_df,
edges_geom,
nodes_geom):
"""Finds closest line to points and returns 2 dataframes:
edges_df
nodes_df
"""
for i in range(len(nodes_df)):
point = nodes_df.loc[i,nodes_geom]
shortest_distance = 100000
for j in range(len(edges_df)):
line = edges_df.loc[j,edges_geom]
if line.distance(point) < shortest_distance:
shortest_distance = line.distance(point)
closest_street_index = j
closest_line = line
...然后,我将结果保存在一个表中,作为一个新列,该列将从点到行的最短路径添加为新列。
有什么方法可以让它更快一些吗?
例如,如果我能过滤掉50米以外的每一个点的线,这将有助于加快每一次迭代的速度?
是否有一种使用rtree包使这一速度更快的方法?我找到了一个能让寻找多边形交集的脚本更快的答案,但我似乎无法使它在最近的一点到线上工作。
https://pypi.python.org/pypi/Rtree/
如果已经回答了,很抱歉,但是我在这里没有找到答案,也没有在gis.stackexchange上找到答案。
谢谢你的建议!
回答 2
Stack Overflow用户
发布于 2017-09-20 16:19:53
这里有一个使用rtree库的解决方案。其思想是构建包含对角线段的框,并使用该框构建rtree。这将是最昂贵的手术。稍后,您使用以点为中心的框查询rtree。您需要检查几次命中的最小值,但是点击的次数(希望地)比检查所有段的次数要低(希望如此)。
在solutions dict中,对于每个点,您将得到直线id、最近的段、最近的点(段的一个点)以及到点的距离。
代码中有一些注释可以帮助您。考虑到您可以序列化rtree以供以后使用。实际上,我建议构建rtree,保存它,然后使用它。因为调整常量MIN_SIZE和INFTY的异常可能会引发,而且您不希望丢失构建rtree的所有计算。
太小的MIN_SIZE将意味着解决方案中可能会有错误,因为如果点周围的框不相交一个段,它可能会交叉一个不是最近段的段(很容易想到一个情况)。
太大的MIN_SIZE意味着有太多的假阳性,在极端情况下,这会使代码对所有段进行尝试,并且您将处于与以前相同的位置,或者最糟糕的情况,因为您现在正在构建一个您并不真正使用的rtree。
如果数据是来自一个城市的真实数据,我想你知道,任何地址都将与一个距离小于几个街区的段相交。这将使搜索几乎是逻辑上的。
再评论一句。我假设没有太大的片段。由于我们使用分段作为rtree中框的对角线,如果在一行中有一些大段,这将意味着将为该段分配一个巨大的框,并且所有的地址框都将它相交。为了避免这种情况,您可以通过添加更多的中间点来人为地提高LineStrins的分辨率。
import math
from rtree import index
from shapely.geometry import Polygon, LineString
INFTY = 1000000
MIN_SIZE = .8
# MIN_SIZE should be a vaule such that if you build a box centered in each
# point with edges of size 2*MIN_SIZE, you know a priori that at least one
# segment is intersected with the box. Otherwise, you could get an inexact
# solution, there is an exception checking this, though.
def distance(a, b):
return math.sqrt( (a[0]-b[0])**2 + (a[1]-b[1])**2 )
def get_distance(apoint, segment):
a = apoint
b, c = segment
# t = <a-b, c-b>/|c-b|**2
# because p(a) = t*(c-b)+b is the ortogonal projection of vector a
# over the rectline that includes the points b and c.
t = (a[0]-b[0])*(c[0]-b[0]) + (a[1]-b[1])*(c[1]-b[1])
t = t / ( (c[0]-b[0])**2 + (c[1]-b[1])**2 )
# Only if t 0 <= t <= 1 the projection is in the interior of
# segment b-c, and it is the point that minimize the distance
# (by pitagoras theorem).
if 0 < t < 1:
pcoords = (t*(c[0]-b[0])+b[0], t*(c[1]-b[1])+b[1])
dmin = distance(a, pcoords)
return pcoords, dmin
elif t <= 0:
return b, distance(a, b)
elif 1 <= t:
return c, distance(a, c)
def get_rtree(lines):
def generate_items():
sindx = 0
for lid, l in lines:
for i in xrange(len(l)-1):
a, b = l[i]
c, d = l[i+1]
segment = ((a,b), (c,d))
box = (min(a, c), min(b,d), max(a, c), max(b,d))
#box = left, bottom, right, top
yield (sindx, box, (lid, segment))
sindx += 1
return index.Index(generate_items())
def get_solution(idx, points):
result = {}
for p in points:
pbox = (p[0]-MIN_SIZE, p[1]-MIN_SIZE, p[0]+MIN_SIZE, p[1]+MIN_SIZE)
hits = idx.intersection(pbox, objects='raw')
d = INFTY
s = None
for h in hits:
nearest_p, new_d = get_distance(p, h[1])
if d >= new_d:
d = new_d
s = (h[0], h[1], nearest_p, new_d)
result[p] = s
print s
#some checking you could remove after you adjust the constants
if s == None:
raise Exception("It seems INFTY is not big enough.")
pboxpol = ( (pbox[0], pbox[1]), (pbox[2], pbox[1]),
(pbox[2], pbox[3]), (pbox[0], pbox[3]) )
if not Polygon(pboxpol).intersects(LineString(s[1])):
msg = "It seems MIN_SIZE is not big enough. "
msg += "You could get inexact solutions if remove this exception."
raise Exception(msg)
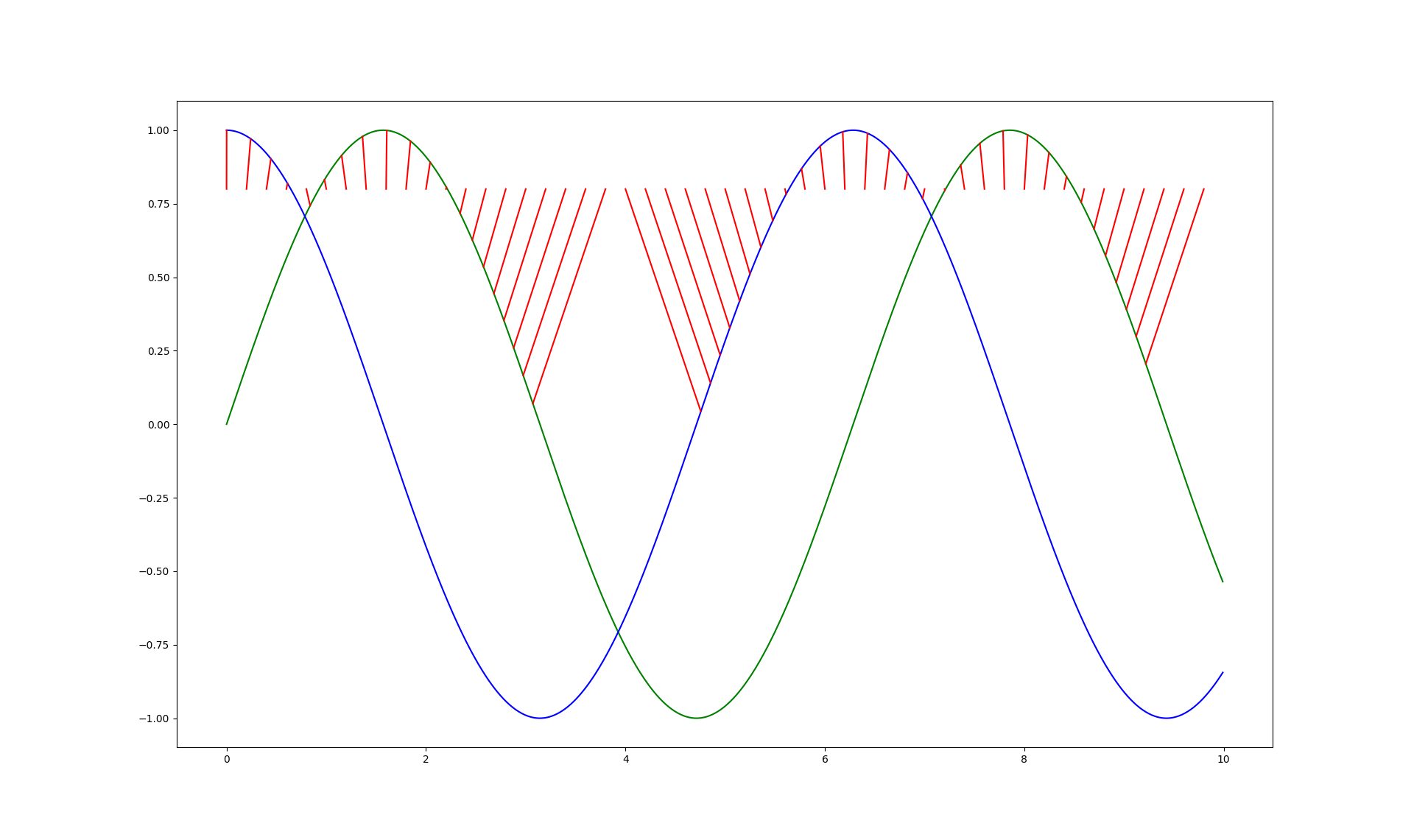
return result我用这个例子测试了这些函数。
xcoords = [i*10.0/float(1000) for i in xrange(1000)]
l1 = [(x, math.sin(x)) for x in xcoords]
l2 = [(x, math.cos(x)) for x in xcoords]
points = [(i*10.0/float(50), 0.8) for i in xrange(50)]
lines = [('l1', l1), ('l2', l2)]
idx = get_rtree(lines)
solutions = get_solution(idx, points)并得到:
Stack Overflow用户
发布于 2020-10-03 23:36:29
我一直在寻找解决方案,我找到了这,它使用Geopandas。基本上,这是一种简单的方法,它考虑点和线的边框的重叠。然而,由于空间索引的存在,计算量明显减少。
https://stackoverflow.com/questions/46170577
复制相似问题

