Python:有向图中的所有简单路径
Python:有向图中的所有简单路径
提问于 2017-09-30 06:48:57
我正在处理一个(数目)没有圈的有向图,我需要在任意两个节点之间找到所有简单的路径。一般来说,我不会担心执行时间,但是我必须在很多时间步骤中对很多节点这样做--我正在处理一个基于时间的模拟。
我过去曾尝试过NetworkX提供的设施,但总的来说,我发现它们比我的方法慢。不知道最近有没有什么变化。
我实现了这个递归函数:
import timeit
def all_simple_paths(adjlist, start, end, path):
path = path + [start]
if start == end:
return [path]
paths = []
for child in adjlist[start]:
if child not in path:
child_paths = all_simple_paths(adjlist, child, end, path)
paths.extend(child_paths)
return paths
fid = open('digraph.txt', 'rt')
adjlist = eval(fid.read().strip())
number = 1000
stmnt = 'all_simple_paths(adjlist, 166, 180, [])'
setup = 'from __main__ import all_simple_paths, adjlist'
elapsed = timeit.timeit(stmnt, setup=setup, number=number)/number
print 'Elapsed: %0.2f ms'%(1000*elapsed)在我的计算机上,平均每次迭代得到1.5ms。我知道这是一个小数目,但我要做很多次这个手术。
如果您感兴趣,我在这里上传了一个包含邻接列表的小文件:
adjlist
我使用邻接列表作为输入,来自NetworkX DiGraph表示。
对算法的改进有什么建议(例如,它必须是递归的吗?)或者我可能尝试的其他方法都是非常受欢迎的。
谢谢。
安德里亚。
回答 1
Stack Overflow用户
回答已采纳
发布于 2017-09-30 07:50:58
您可以通过缓存共享子问题的结果来节省时间,而无需更改算法逻辑。
例如,在下面的图中调用all_simple_paths(adjlist, 'A', 'D', [])将多次计算all_simple_paths(adjlist, 'D', 'E', []):
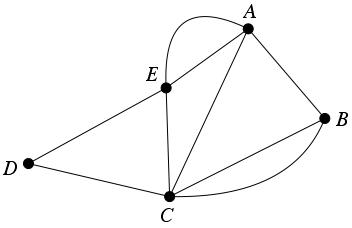
Python有一个内置的装饰器lru_cache来完成这个任务。它使用哈希来记忆参数,因此您需要将adjList和path更改为tuple,因为list是不可接受的。
import timeit
import functools
@functools.lru_cache()
def all_simple_paths(adjlist, start, end, path):
path = path + (start,)
if start == end:
return [path]
paths = []
for child in adjlist[start]:
if child not in path:
child_paths = all_simple_paths(tuple(adjlist), child, end, path)
paths.extend(child_paths)
return paths
fid = open('digraph.txt', 'rt')
adjlist = eval(fid.read().strip())
# you can also change your data format in txt
adjlist = tuple(tuple(pair)for pair in adjlist)
number = 1000
stmnt = 'all_simple_paths(adjlist, 166, 180, ())'
setup = 'from __main__ import all_simple_paths, adjlist'
elapsed = timeit.timeit(stmnt, setup=setup, number=number)/number
print('Elapsed: %0.2f ms'%(1000*elapsed))在我的机器上运行时间:
- 原件: 0.86ms
- 带缓存: 0.01ms
这种方法只有在有很多共享子问题时才能起作用。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/46500318
复制相关文章
相似问题

