为什么9x9 . slower的方法在9x9矩阵上运行得更慢?
为什么9x9 . slower的方法在9x9矩阵上运行得更慢?
提问于 2017-10-09 22:25:49
我正在比较各种解决线性系统的方法的运行时,我发现了一个奇怪的模式。我正在测试的解决方案方法是la.solve()、la.inv()和la.lu_factor_solve()。
import scipy.linalg as la
import numpy as np
from time import time
from matplotlib import pyplot as plt
N = 20 # up to NxN matrix
T = 100 # run T times
inv_time, solve_time = [[] for _ in range(20)], [[] for _ in range(20)]
lu_factor_solve, lu_just_solve = [[] for _ in range(20)], [[] for _ in range(20)]
for _ in range(T):
for n in range(1, N + 1):
A = np.random.rand(n, n)
b = np.random.rand(n, 1)
np.dot(la.inv(A), b) # the first time through is always slow,
la.solve(A, b) # so we run it once to get it out of the way
start = time()
np.dot(la.inv(A), b)
end = time()
inv_time[n - 1].append(end - start)
start = time()
la.solve(A, b)
end = time()
solve_time[n - 1].append(end - start)
start = time()
la.lu_solve(la.lu_factor(A), b)
end = time()
lu_factor_solve[n - 1].append(end - start)
temp = la.lu_factor(A)
start = time()
la.lu_solve(temp, b)
end = time()
lu_just_solve[n - 1].append(end - start)
inv_time = np.mean(np.array(inv_time), axis=1)
solve_time = np.mean(np.array(solve_time), axis=1)
lu_factor_solve = np.mean(np.array(lu_factor_solve), axis=1)
lu_just_solve = np.mean(np.array(lu_just_solve), axis=1)
# do some plots
plt.plot(range(1, N + 1), inv_time, '-o', label='by inverse')
plt.plot(range(1, N + 1), solve_time, '-o', label='by la.solve()')
plt.plot(range(1, N + 1), lu_factor_solve, '-o', label='by lu factor solve')
plt.yscale('log')
plt.plot(range(1, N + 1), lu_just_solve, '-o', label='just la.lu_solve()')
plt.legend()
plt.show()这些是在随机矩阵A上运行的,以及A = np.random.rand(n, n)和b = np.random.rand(n, 1)为n值从1到20之间生成的列向量b。我发现,每当我运行程序时,它都会找到9x9矩阵的解决方案,比其他大小的矩阵要慢得多,如下图所示。红线显示执行la.lu_solve()所需的时间。下面是T = 1的结果图:
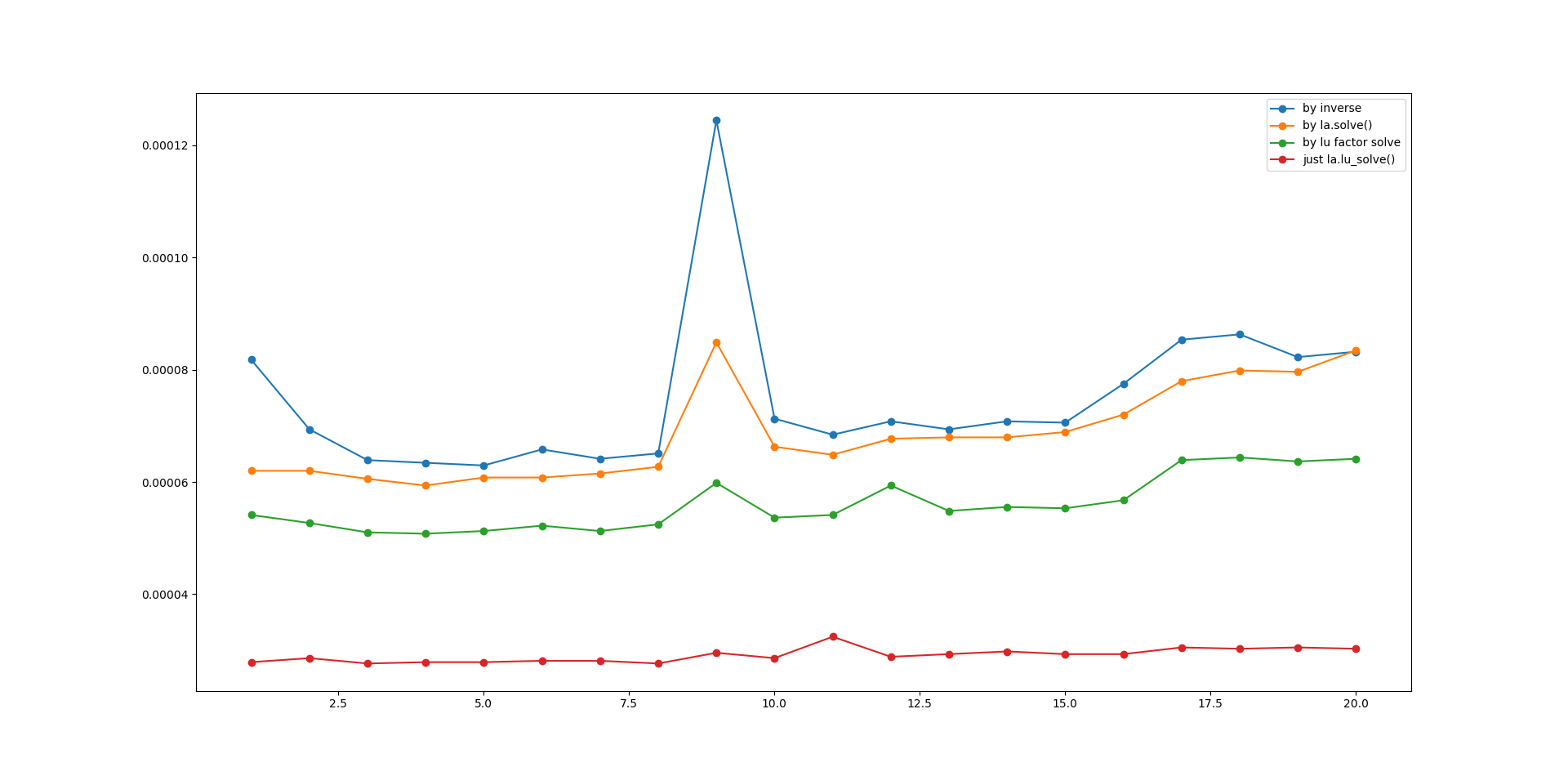
下面是T = 100的结果:
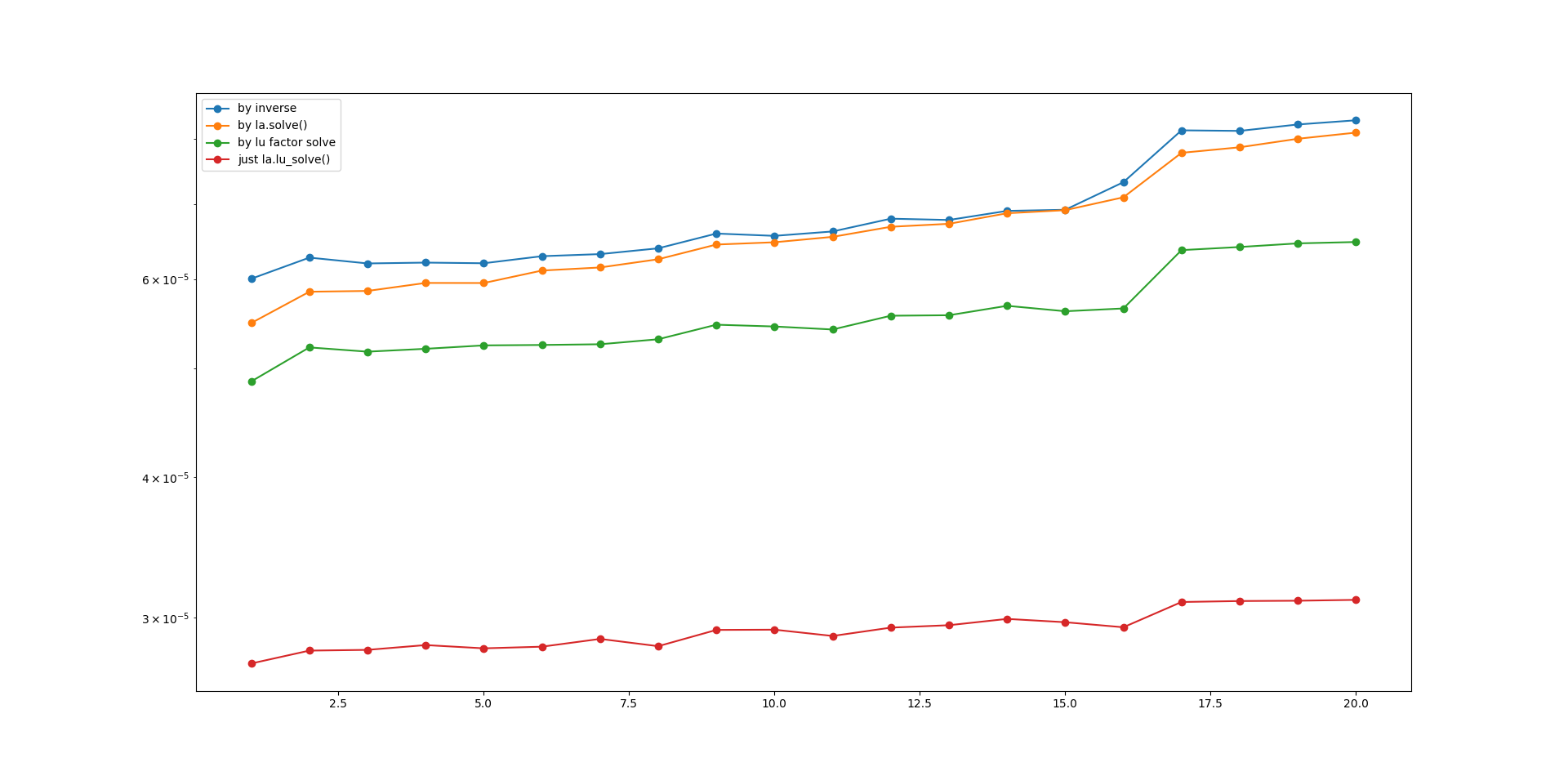
这是否与9x9矩阵的固有特性有关,对于这样的矩阵大小是不可用的一些优化,还是与某些不同的东西有关?
回答 1
Stack Overflow用户
回答已采纳
发布于 2017-10-09 23:03:38
我已经用完成图 (我的一个小项目,本质上是一个时间包装器)尝试了您的代码示例,但没有发现这样的特性。但是,人们可以识别级别1缓存的耗尽:
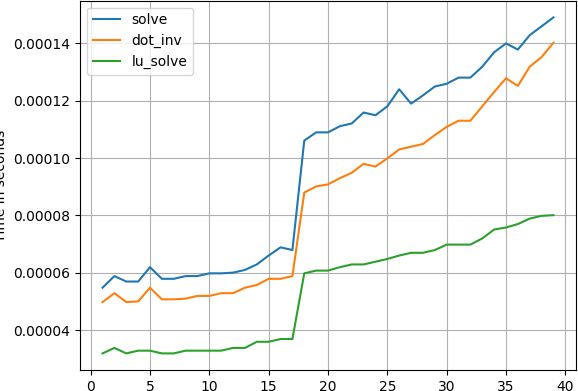
这与NumPy 1.13.3和SciPy 1.0.0rc1一起使用。
当只运行一次测试时,代码示例中会出现尖峰,原因是它们运行得太快,以至于对机器其他部分的小干扰可能变得很大。这可能是从浏览器中的JS引擎到CPU从更深的睡眠状态中醒来的重复任务。你在n=9看到这些尖峰是个巧合。当我只运行一次测试时,我自己可以在5到20之间的任何地方复制随机的峰值。
再现情节的代码:
import numpy
import perfplot
import scipy.linalg as la
def solve(data):
A, b = data
return la.solve(A, b)
def dot_inv(data):
A, b = data
return numpy.dot(la.inv(A), b)
def lu_solve(data):
A, b = data
return la.lu_solve(la.lu_factor(A), b)
perfplot.show(
setup=lambda n: (numpy.random.rand(n, n), numpy.random.rand(n)),
kernels=[solve, dot_inv, lu_solve],
n_range=range(1, 40),
)页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/46655873
复制相关文章
相似问题

