参数评分函数或算法
参数评分函数或算法
提问于 2017-10-13 13:13:42
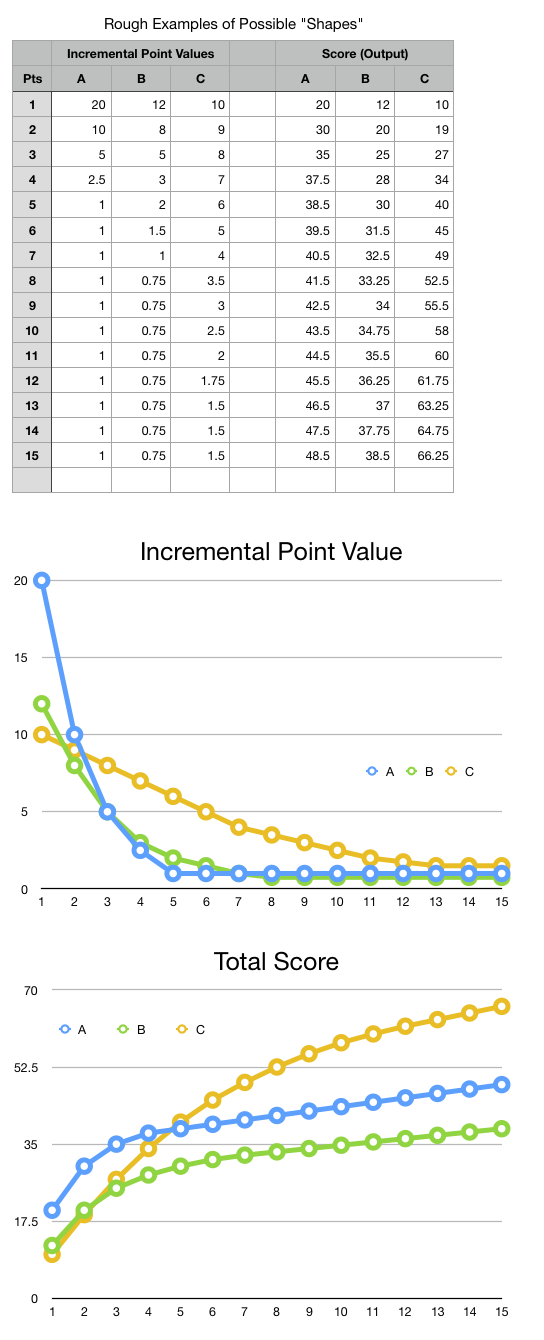
我试图想出一种方法,根据一个整数的“点数”来得出一个“分数”,这个整数是用一个小数字(3-5?)来调节的。关于参数的。最好是足够简单,可以在电子表格中合理地输入函数/计算,由"designer“(而不是程序员或数学家)调优参数。第一点有最大的价值,最终附加点有一个固定的或几乎固定的值。从点值的初始斜率到最终坡度的过渡将是平稳的。见下面的示例形状。
- 积分值总是正整数(0pt=0分)。
- 在某个点,曲线是线性的(或接近),所有附加点都有固定的值。
- 如:“曲线的光滑性”、“第一点的值”、“点的附加值固定的地方”等。
对于参数,理想情况的一个例子是:
- 第一点的值:
10 - 点的值#:
3是:5 - 附加点的最小值:
0.75
曲线的精确形状不太重要,只要拐角可以更光滑或更锐利。
这不是一个游戏,但更多的评级系统与多个组成部分(其中有几个可能使用这种规模)将合并。
对于SO/SE来说,这似乎是一个非传统的问题。在我的职业生涯中,我主要做的是金融软件,我希望在这种事情上我能得到一些领域的智慧。
执行Prune的解决方案:

回答 1
Stack Overflow用户
回答已采纳
发布于 2017-10-13 23:04:34
参数:
- 初值(a)
- 第二值(b)
- 最小值(z)
你的衰减率是b/a。从这里开始很简单:迭代你的值,在每一步应用衰变,直到你“钉住”到最小:
x[n] = max( z, a * (b/a)^n )
// Take the larger of the computed "decayed" value,
// and the specified minimum.序列x是您的值列表。
如果希望整数达到某个点,还可以截断中间结果。只需将地板函数应用于每个计算值,但仍然允许z在太小的情况下覆盖该值。
这就够了吗?我知道导数函数有一个不连续性,如果极小和衰变不能很好地对齐,它就会很明显。您可以通过相对衰减来调整这一点,将指数衰减曲线从y=0转换为z。
base = z
diff = a-z
ratio = (b-z) / diff
x[n] = z + diff * ratio^n在这种情况下,您不需要最大函数,因为衰变的自然渐近线为0。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/46730833
复制相关文章
相似问题

