在MATLAB中将图像矩阵围绕其中心旋转
假设我有一个2x2矩阵,其中充满了表示平面的值。现在我想让飞机以三维的方式旋转,在“z-方向”。要获得更好的理解,请参见以下图像:
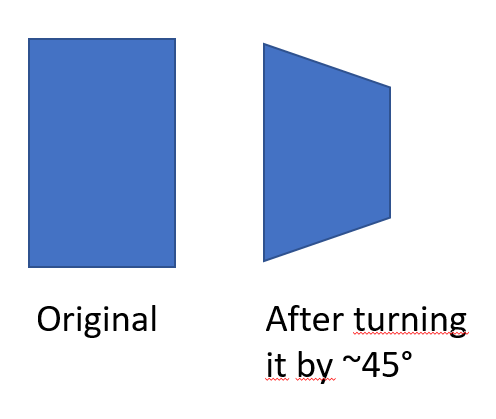
我想知道这是否可以通过一个简单的仿射矩阵来实现,因此我创建了以下简单脚本:
%Create a random value matrix
A = rand*ones(200,200);
%Make a box in the image
A(50:200-50,50:200-50) = 1;现在,我可以简单地通过这样的旋转矩阵在二维房间中应用转换:
R = affine2d([1 0 0; .5 1 0; 0 0 1])
tform = affine3d(R);
transformed = imwarp(A,tform);然而,这不会产生上述期望的输出,我不太确定如何创建二维仿射矩阵来创建这样的行为。
我想三维仿射矩阵可以做到这一点。但是,如果我定义了一个三维仿射矩阵,我就不能再使用矩阵的二维表示了,因为MATLAB会抛出错误:
The number of dimensions of the input image A must be 3 when the
specified geometric transformation is 3-D.那么,我如何用仿射矩阵编码所需的输出呢?
回答 2
Stack Overflow用户
发布于 2017-11-15 16:42:56
来自m3tho的回答正确地说明了如何应用所需的转换:将fitgeotrans与转换一起使用,因此需要指定4个控制点(即输入和输出图像中的4对对应点)。然后可以使用imwarp应用此转换。
因此,问题在于如何选择这些对点来创建所需的转换,在本例中是创建一个透视投影。如下图所示,透视投影考虑到观看位置(即“照相机”)将具有定义圆锥视野的给定视角。场景是通过在这个锥内的所有三维点并将它们投影到观察平面上来呈现的,这是位于摄像机目标处的平面,它垂直于连接摄像机及其目标的直线。
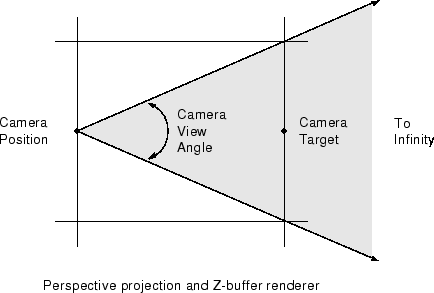
让我们首先假设您的图像位于视图平面上,并且这些角是由一个标准化的参考框架描述的,因此它们在每个方向上都跨越[-1 1]。我们首先需要通过选择一个视角来选择我们想要的透视度,然后计算摄像机和观察平面之间的距离。一个45度左右的视角可以模拟正常人类视觉的透视感,因此利用观察平面的角来定义圆锥形视场的边缘,我们可以计算出摄像机的距离如下:
camDist = sqrt(2)./tand(viewAngle./2);现在,我们可以使用它为转换生成一组控制点。我们首先将一个三维旋转应用到观察平面的角点上,在y轴上旋转一定量的theta。这会将它们从平面上旋转出来,所以我们现在将角点投影回观看平面,通过每个旋转的角点和找出它与平面相交的点,从摄像机中定义一条线。我将省去数学推导(您可以自己从上面链接中的公式中实现它们),但是在这种情况下,一切都简化到以下几组计算:
term1 = camDist.*cosd(theta);
term2 = camDist-sind(theta);
term3 = camDist+sind(theta);
outP = [-term1./term2 camDist./term2; ...
term1./term3 camDist./term3; ...
term1./term3 -camDist./term3; ...
-term1./term2 -camDist./term2];outP现在在输出映像中包含标准化的控制点集。给定大小为s的图像,我们可以创建一组输入和输出控制点,如下所示:
scaledInP = [1 s(1); s(2) s(1); s(2) 1; 1 1];
scaledOutP = bsxfun(@times, outP+1, s([2 1])-1)./2+1;您可以像这样应用转换:
tform = fitgeotrans(scaledInP, scaledOutP, 'projective');
outputView = imref2d(s);
newImage = imwarp(oldImage, tform, 'OutputView', outputView);你可能会遇到的唯一问题是,90度的旋转(即看着图像平面结束)会产生一组共线点,从而导致fitgeotrans出错。在这种情况下,从技术上讲,你只想要一个空白的图像,因为当你看到一个二维物体时,你不能看到它的边缘。
下面是一些代码,通过动画来演示上面的转换:
img = imread('peppers.png');
s = size(img);
outputView = imref2d(s);
scaledInP = [1 s(1); s(2) s(1); s(2) 1; 1 1];
viewAngle = 45;
camDist = sqrt(2)./tand(viewAngle./2);
for theta = linspace(0, 360, 360)
term1 = camDist.*cosd(theta);
term2 = camDist-sind(theta);
term3 = camDist+sind(theta);
outP = [-term1./term2 camDist./term2; ...
term1./term3 camDist./term3; ...
term1./term3 -camDist./term3; ...
-term1./term2 -camDist./term2];
scaledOutP = bsxfun(@times, outP+1, s([2 1])-1)./2+1;
tform = fitgeotrans(scaledInP, scaledOutP, 'projective');
spinImage = imwarp(img, tform, 'OutputView', outputView);
if (theta == 0)
hImage = image(spinImage);
set(gca, 'Visible', 'off');
else
set(hImage, 'CData', spinImage);
end
drawnow;
end这是动画:

Stack Overflow用户
发布于 2017-11-13 23:13:54
您可以执行投影转换,该转换可以使用第一和第二图像中角的位置来估计。
originalP='peppers.png';
original = imread(originalP);
imshow(original);
s = size(original);
matchedPoints1 = [1 1;1 s(1);s(2) s(1);s(2) 1];
matchedPoints2 = [1 1;1 s(1);s(2) s(1)-100;s(2) 100];
transformType = 'projective';
tform = fitgeotrans(matchedPoints1,matchedPoints2,'projective');
outputView = imref2d(size(original));
Ir = imwarp(original,tform,'OutputView',outputView);
figure; imshow(Ir);这是上述代码的结果:
原始图像:

变换后的图像:

https://stackoverflow.com/questions/47273993
复制相似问题

