问剪切旋转的任意角度(Paeth算法)

EN

我试图编写一个3剪切旋转算法阿兰·佩思的Java实现。问题不是值的计算，而是将旋转点拟合到图像网格上。在本文中，旋转是通过下列计算给出的三个连续剪刀进行的：

1. X=x+ alpha *y
2. y= y+β*x
3. X=x+ alpha *y

α和β是根据给定的角度(θ；半径)计算的，公式如下：

• β=sin(θ)
• alpha =-tan(θ/2)

利用这些公式，点围绕着坐标系的中心旋转。

为了纠正负值，我将相应轴的最小计算坐标添加到每个点，使最小值始终为0。

到目前为止，我的Java实现：

ShiftPoint[] val = new ShiftPoint[m*n];
double minX = 0,minY = 0, maxX = 0, maxY = 0;
double alpha = -1d*  Math.tan(Math.toRadians(theta)/2d);
double beta = Math.sin(Math.toRadians(theta));
for(int a = 0; a < m; a++) {
    for(int b = 0; b < n; b++) {
        ShiftPoint temp = new ShiftPoint(a, b, values[a][b]);
        double newX = b + alpha * a;    //first shear
        double newY = a + beta * newX;  //second shear
        newX += alpha * newY;           //third shear
        temp.setX(newX);
        temp.setY(newY);
        val[m * b + b] = temp;
    }
}

注意: ShiftPoint是一个简单的自写类，用于保存特定坐标和矩阵中的值(在图像处理中:像素的rgb值)。下面是计算的图形表示：

​

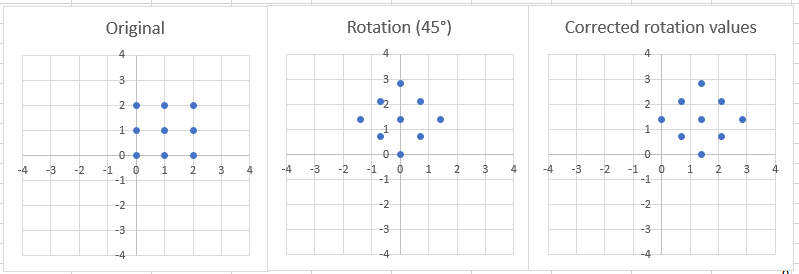
问题:虽然计算值似乎是正确的，并且图形表示显示旋转实际上是有效的，但我不知道如何在固定网格上拟合计算值--图像(或2d数组)--不失真它。此外，我也不完全理解Paeth文件中给出的实现(对于x轴剪切)：

​

​

我得到，斜交是计算值的整数部分，斜交是分数部分，但是宽度、高度、烯烃和左边长是多少呢？另外:为什么他在第一次计算时将y值加到0.5，而不考虑x值？

注意:我知道Java提供了简单的旋转图像的方法，但是为了好玩，我尝试实现这个特定的算法。我还知道有3-5个网站可以通过网络搜索(如#1和#2)找到，并试图解释该算法，但首先它们不使用java，其次它们主要引用Paeth的示例实现，因此它们不是很有用。