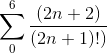问获得e值最快的方法是什么？

EN

1. 基本数据类型 正如注释中提到的，6-7小数位太小，不能通过算法实现。相反，使用常量，这是最快的方式无论如何。 const双e=2.7182818284590452353602874713527； 如果涉及FPU，则常数通常也存储在那里.还有一个常数所占的空间比计算它的函数少得多.
2. 有限精度 只有一旦涉及到bignum，那么使用算法计算e就有任何优点了。航向取决于目标的准确性。同样，对于较小的准确性，也使用了预定义的常量： e=2.71828182845904523536028747135266249775724709369995957496696762772407663035354759457138217852516642742746639193200305992181741359662904357290033429526059563073813232862794349076323382988075319525101901157383418793070215408914993488416750924476146066808226480016847741185374234544243710753907774499206955170189 但通常以十六进制格式进行更快和更精确的操作： e=2.B7E151628AED2A6ABF7158809CF4F3C762E7160F38B4DA56A784D9045190CFEF324E7738926CFBE5F4BF8D8D8C31D763DA06C80ABB1185EB4F7C7B5757F5958490CFD47D7C19BB42158D9554F7B46BCED55C4D79FD5F24D6613C31C3839A2DDF8A9A276BCFBFA1C877C56284DAB79CD4C2B3293D20E9E5EAF02AC60ACC93ECEBh 对于有限的/有限的精度和最佳的速度，PSLQ算法是最好的。我的理解是，寻找实数和整数迭代之间的关系是一种算法。

- [here is my favourite PSLQ up to 800 digits of Pi PSLQ example](https://cs.uwaterloo.ca/~alopez-o/math-faq/mathtext/node12.html)

​

1. 任意精度 对于任意或“固定”的精度，您需要具有可变精度的算法。这是我在我的arbnum类中使用的： e=(1+1/x)^x其中x -> +无穷大 如果选择x作为2的幂，请注意，x只是数字的单个集合位，而1/x具有可预测的位宽。因此，用单除法和pow法就可以得到pow。这里有一个例子： arithmetics_e() // e计算min(_arbnum_max_a，arbnum_max_b)*5个小数{ // e=(1+1/x)^x .X -> +inf int i；arbnum c，x；i=_arbnum_bits_a；if (i>_arbnum_bits_b) i=_arbnum_bits_b；i>>=1；c.zero()；c.bitset(_arbnum_bit_b-i)；x.one()；x/=c；c++；for (！x.bitget(_arbnum_bits_b)；x>>=1) c*=c；//=pow(c，x)；返回c；} 其中_arbnum_bits_a,_arbnum_bits_b是二进制小数点前后的位数。因此，它分解为一些位操作，一个大除法和一个幂平方。请注意，乘法和除法并没有那么简单，通常涉及到Karatsuba或更糟的. 还有一些多项式方法不需要类似于计算bignum的Pi算法。其思想是每次迭代计算二进制位块，而不影响先前计算过的比特(太多)。它们应该更快，但对于任何依赖于实现和运行的HW的优化，它们应该是正常的。

​

​

如需参考，请参阅兄弟的公式：https://www.intmath.com/exponential-logarithmic-functions/calculating-e.php