问图论Cutwidth

EN

您的定义有点不完整:您还应该包括与图的排序相关的成本的定义。在您可能要引用的定义中，此成本定义如下：

对于任何节点集S，相应的代价c'(S)是由S中的任何节点到S之外的任何节点的边数所给出的。

由此，排序v_1, ..., v_n的成本被定义为所有子集v_1, ..., v_i的最大成本，其中i = 1, ..., n - 1

根据前面的定义，这意味着从低阶节点到高阶节点的最大边数，您可以任意地在低阶和高阶之间选择“裁剪”。

然后是节点最优排序的代价(即成本最小的节点排序)。

当我们将此应用于区间图时，这意味着一个图的节点是区间，其边表示这些区间之间的交点，子集的代价c'( S )是S以外区间与S内间隔之间的交叉点数。

由此，你可以看到，区间图的顶点是区间最优排序的代价，这样高阶区间与低阶区间相交的次数最少。

不幸的是，对于给定的区间图，我不能给出一个精确的计算规则，但是我将给出一个小的例子：

取间隔0,4,0,1,2,3,1.5,2.5,3.5,5，给出如下图表：

​

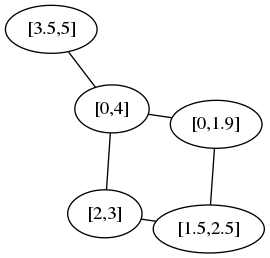
无论您如何排序间隔，如果您选择了4个周期中的两个区间(0、4、0、1.9、1.5、2.5、2、3)，则循环中的其他两个区间将至少有两个与前两个区间的交叉点，这意味着至少为2。

同时，排序0,1.9,1.5,2.5,2,3,0,4,3.5,5给出了2,2,2,1对于i = 1,2,3,4的削减成本，所以这个图的顶点最多是2。

结合这些结果，你可以看到图的角速度是2。

也许可以把这类上界和下界推广到所有区间图，但我现在还不能给出这个问题的完整解。