如何解释scipy.stats.probplot结果?
我想用scipy.stats.probplot()在mydata上做一些测试。
from scipy import stats
_,fit=stats.probplot(mydata, dist=stats.norm,plot=ax)
goodness_fit="%.2f" %fit[2]文件上说:
根据指定理论分布的分位数(缺省情况下为正态分布)生成样本数据的概率图。可以选择计算数据的最佳匹配行,并使用Matplotlib或给定的绘图函数绘制结果。概率图生成一个概率图,,不应与Q-Q或P图混淆。Statsmodels具有这种类型的更广泛的功能,请参见statsmodels.api.ProbPlot。
但是如果google 概率图,它是P图的一个通用名称,而文档中说不要混淆这两件事。
现在我很困惑,这个功能是做什么的?
回答 2
Stack Overflow用户
发布于 2019-04-29 20:59:28
我从几个小时以来就一直在寻找这个问题的答案,这可以在Scipy/Statsmodel代码注释中找到。
在Scipy中,https://github.com/scipy/scipy/blob/abdab61d65dda1591f9d742230f0d1459fd7c0fa/scipy/stats/morestats.py#L523的评论说:
probplot生成概率图,不应与Q-Q或P图混淆.Statsmodels具有这种类型的更广泛的功能,请参见statsmodels.api.ProbPlot。
现在,让我们来看看Statsmodels,https://github.com/statsmodels/statsmodels/blob/66fc298c51dc323ce8ab8564b07b1b3797108dad/statsmodels/graphics/gofplots.py#L58的评论是这样说的:
概率图:概率图比较样本和理论概率(百分位数). qqplot :分位数图比较样本和理论分位数。 概率图:概率图与Q-Q图相同,但概率在理论分布(x轴)的尺度上显示,y轴包含样本数据的无标度分位数。
因此,在这些模块中,QQ图和概率图的差异与量表有关。
Stack Overflow用户
发布于 2019-11-20 07:53:59
事件发生的理论概率是基于对情况的了解的“预期”概率。它是转正有利结果的数量与可能结果的数量。
在实验期间,当你从观测数据中收集数据时,你将计算一个更接近的经验概率(或实验概率)。
示例:你抛出一枚硬币,你得到了一个头。
- 实验概率(头)=1
- 理论概率(头)=0.5
为了简单起见,请参阅下图,该图显示获得特定票据金额的概率。给出了P图和Q图。
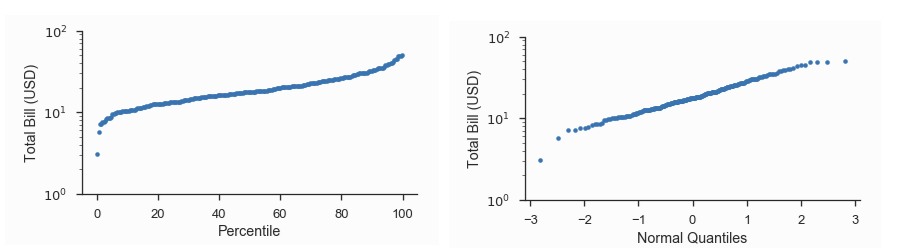
概率图(概率概率图)
- 比较样本和理论概率(百分位数)。
qqplot (分位数图)
- 比较样本和理论分位数
概率图(概率图)
- 然而,与Q-Q图一样,概率在理论分布(x-轴)的尺度上显示,y-轴包含样本数据的无标度分位数。
to、qqplot和概率图的差异与量表有关。在x轴和y轴上都显示了样品和理论值。
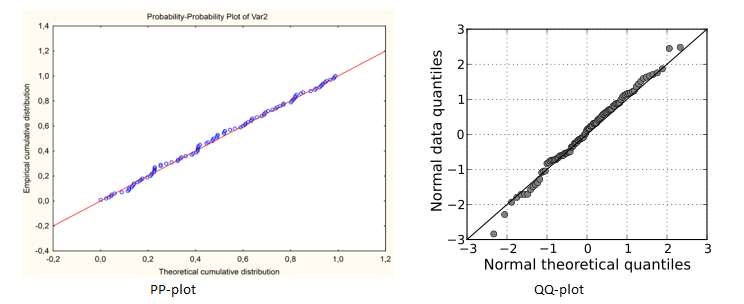
百分位数图
- 百分位图是最简单的情节。您只需根据他们的绘图位置绘制数据。绘图位置显示在线性尺度上,但数据可以适当地进行缩放。
分位图
- 分位数图与概率图相似。主要的区别是绘图位置被转换成基于概率分布的分数或ZZ分数。
默认分布是标准正态分布.您会注意到,在Q图上,数据的形状比P图更直观。这是由于在将绘图位置转换为分布的分位数时发生的转换。
最佳匹配线
- 在概率图中添加一条最佳拟合线可以提供数据集是否可以用分布来描述的洞察力。
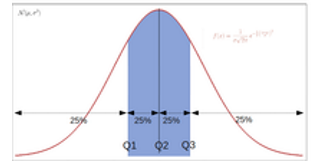
在统计量和概率分位数中,等分位数是将概率分布的范围划分为具有相同概率的连续区间的切分点,或者用同样的方式将观测值分割成一个样本。
正态分布的概率密度,四分位数显示。红色曲线下的区域在间隔(−∞,Q1),(Q1,Q2),(Q2,Q3)和(Q3,+∞)中是相同的。
在统计学中,Q(分位数)图是一种相似概率图,它是一种比较两种相似概率分布的图解方法。
如果比较的两个分布相似,那么Q-Q图中的点将近似位于line y = x上,如果分布是线性相关的,则Q-Q图中的点将近似位于一条线上,但不一定位于line y = x上。
Q-Q图用于比较分布的形状,提供了一个图形视图,说明在这两种分布中,诸如位置、规模和倾斜度等属性是如何相似或不同的。
P-P图两个相对的累积分布函数(Cdfs):它是一个评估两个相似数据集是否一致的概率图,它将两个基本的累积分布函数(Cdf)相提并论。P图被广泛地用于评价分布的倾斜度.
https://stackoverflow.com/questions/48108582
复制相似问题

