R中的学习隐马尔可夫模型
隐马尔可夫模型(HMM)是一种观察序列,但不知道模型经过的状态序列来产生观测。隐马尔可夫模型的分析试图从观测数据中恢复隐藏状态的序列。
我有观察和隐藏状态的数据(观测值是连续的),其中隐藏状态是由专家标记的。我想训练一个HMM,它将能够--基于一个(以前看不见的)观察序列--恢复相应的隐藏状态。
有什么R包可以做到吗?研究现有的包(depmixS4、HMM、seqHMM -仅针对分类数据)允许您仅指定一些隐藏状态。
编辑:
示例:
data.tagged.by.expert = data.frame(
hidden.state = c("Wake", "REM", "REM", "NonREM1", "NonREM2", "REM", "REM", "Wake"),
sensor1 = c(1,1.2,1.2,1.3,4,2,1.78,0.65),
sensor2 = c(7.2,5.3,5.1,1.2,2.3,7.5,7.8,2.1),
sensor3 = c(0.01,0.02,0.08,0.8,0.03,0.01,0.15,0.45)
)
data.newly.measured = data.frame(
sensor1 = c(2,3,4,5,2,1,2,4,5,8,4,6,1,2,5,3,2,1,4),
sensor2 = c(2.1,2.3,2.2,4.2,4.2,2.2,2.2,5.3,2.4,1.0,2.5,2.4,1.2,8.4,5.2,5.5,5.2,4.3,7.8),
sensor3 = c(0.23,0.25,0.23,0.54,0.36,0.85,0.01,0.52,0.09,0.12,0.85,0.45,0.26,0.08,0.01,0.55,0.67,0.82,0.35)
)我想要创建一个带有离散时间t的HMM,其中随机变量x(t)表示时间t,x(t)的隐藏状态。
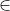
{"Wake“、"REM”、"NonREM1“、"NonREM2"}和3个连续随机变量sensor1( t )、sensor2(t)、sensor3(t)表示时间t的观测值。
model.hmm = learn.model(data.tagged.by.user)然后,我想使用创建的模型来估计对新测量的观测负责的隐藏状态。
hidden.states = estimate.hidden.states(model.hmm, data.newly.measured)回答 1
Stack Overflow用户
发布于 2018-07-11 17:43:47
数据(培训/测试)
为了能够运行朴素贝叶斯分类器的学习方法,我们需要更长的数据集。
states = c("NonREM1", "NonREM2", "NonREM3", "REM", "Wake")
artificial.hypnogram = rep(c(5,4,1,2,3,4,5), times = c(40,150,200,300,50,90,30))
data.tagged.by.expert = data.frame(
hidden.state = states[artificial.hypnogram],
sensor1 = log(artificial.hypnogram) + runif(n = length(artificial.hypnogram), min = 0.2, max = 0.5),
sensor2 = 10*artificial.hypnogram + sample(c(-8:8), size = length(artificial.hypnogram), replace = T),
sensor3 = sample(1:100, size = length(artificial.hypnogram), replace = T)
)
hidden.hypnogram = rep(c(5,4,1,2,4,5), times = c(10,10,15,10,10,3))
data.newly.measured = data.frame(
sensor1 = log(hidden.hypnogram) + runif(n = length(hidden.hypnogram), min = 0.2, max = 0.5),
sensor2 = 10*hidden.hypnogram + sample(c(-8:8), size = length(hidden.hypnogram), replace = T),
sensor3 = sample(1:100, size = length(hidden.hypnogram), replace = T)
)解决方案
在解决方案中,我们采用了Viterbi算法-结合朴素贝叶斯分类器。
在每个时钟时刻t,隐马尔可夫模型包括
- 一种未观察到的状态(在本例中表示为hidden.state ),其状态数目有限 states = c("NonREM1“、"NonREM2”、"NonREM3“、"REM”、"Wake")
- 一组观察到的变量(本例中为sensor1、sensor2、sensor3 )
过渡矩阵
基于转移概率分布进入一个新的状态。
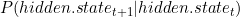
(变换矩阵)。这可以很容易地从data.tagged.by.expert中计算,例如使用
library(markovchain)
emit_p <- markovchainFit(data.tagged.by.expert$hidden.state)$estimate发射矩阵
在每个过渡之后,根据条件概率分布产生一个观测(sensor_i)。
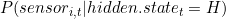
(发射矩阵),它只依赖于hidden.state的当前状态H。我们将用朴素贝叶斯分类器代替发射矩阵。
library(caret)
library(klaR)
library(e1071)
model = train(hidden.state ~ .,
data = data.tagged.by.expert,
method = 'nb',
trControl=trainControl(method='cv',number=10)
)Viterbi算法
为了解决这个问题,我们使用初始概率为1的Viterbi算法表示“唤醒”状态,否则使用0。(我们期望病人在实验开始时醒着)
# we expect the patient to be awake in the beginning
start_p = c(NonREM1 = 0,NonREM2 = 0,NonREM3 = 0, REM = 0, Wake = 1)
# Naive Bayes model
model_nb = model$finalModel
# the observations
observations = data.newly.measured
nObs <- nrow(observations) # number of observations
nStates <- length(states) # number of states
# T1, T2 initialization
T1 <- matrix(0, nrow = nStates, ncol = nObs) #define two 2-dimensional tables
row.names(T1) <- states
T2 <- T1
Byj <- predict(model_nb, newdata = observations[1,])$posterior
# init first column of T1
for(s in states)
T1[s,1] = start_p[s] * Byj[1,s]
# fill T1 and T2 tables
for(j in 2:nObs) {
Byj <- predict(model_nb, newdata = observations[j,])$posterior
for(s in states) {
res <- (T1[,j-1] * emit_p[,s]) * Byj[1,s]
T2[s,j] <- states[which.max(res)]
T1[s,j] <- max(res)
}
}
# backtract best path
result <- rep("", times = nObs)
result[nObs] <- names(which.max(T1[,nObs]))
for (j in nObs:2) {
result[j-1] <- T2[result[j], j]
}
# show the result
result
# show the original artificial data
states[hidden.hypnogram]参考文献
欲了解更多关于这一问题的资料,请参阅Vomlel Jiří,Kratochvíl Václav : Dynamic Stages for the分类法睡眠阶段,第11期不确定性处理讲习班会议记录(WUPES‘18),第205至215页,Eds: Kratochvíl Václav,VejnarováJiřina,不确定性处理讲习班(WUPES’18),(Třeboň,CZ,2018年/06/06)2018年
https://stackoverflow.com/questions/48341856
复制相似问题

