问具有离散自变量的非线性回归

EN

结果发现，我有两个变量不满足线性假设。因变量是连续的，自变量是数值离散的。在这里，剩余的情节和一个盒子和胡须图：

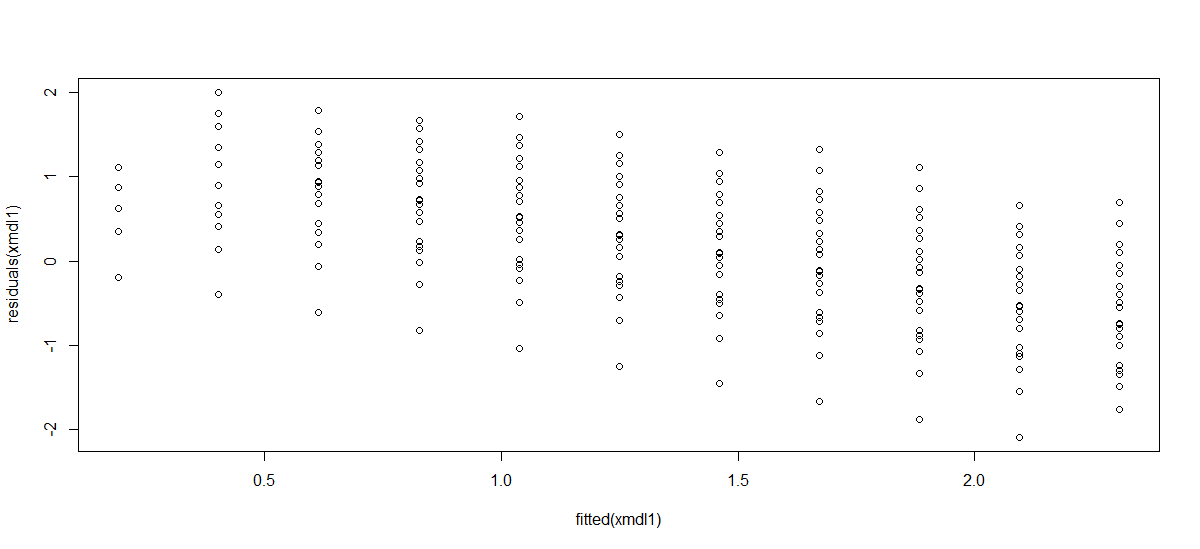
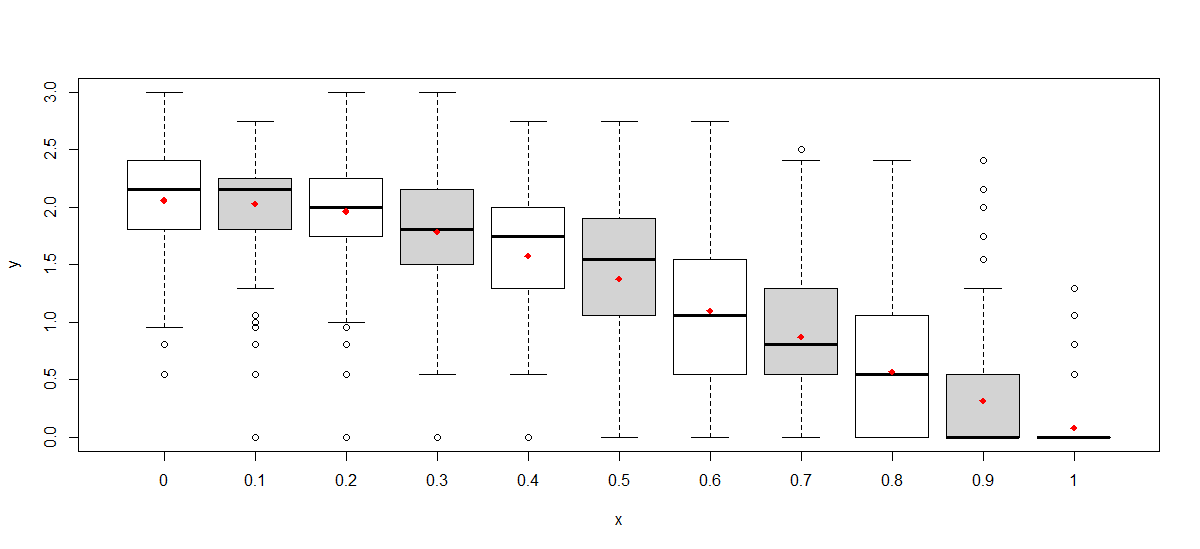
因此，我不能用线性回归。我试图通过转换数据(通过执行log(y)；log(x)；sqrt(y)；等等)将变量之间的关系线性化，但没有成功。我没有发现任何能令人满意地增加线性度的变换。因此，我最终试图将非线性函数与我的数据相结合(对我来说，这是一个完全未知的领域，我在互联网上找不到很多信息)。因此，我想知道我是否采取了正确的步骤来进行非线性分析：

1)我做的第一件事就是选择二次多项式。

y = a + (b*x) + c*(x^2)

这是我的第一个疑问(使用什么功能？)因为我知道有很多不同的函数可以描述同一条线。

2)第二件事是用非线性最小二乘法(R中的函数nls )估计参数，它基本上是用线性函数逼近非线性函数，并迭代地试图找到最佳的参数值：

m <- nls(y ~ a + (b*x) + c*(x^2), start= list(a = 2, b = 1, c=1))

要为参数选择初始值(开始)，我尝试选择接近预期最终解决方案的初始值。尽管我发现，即使我改变了初始值，最终的结果仍然是一样的。以下是非线性最小二乘法后的参数估计值：

非线性回归模型:y~a+ (b * x) +c* (x^2)数据: parent.frame() a b_c 2.1296 -0.9395 -1.1754剩余平方和: 27615次迭代到收敛:1达到收敛容限: 2.58e-08

3)最后，通过summary(m)检查结果。

公式:y~a+ (b * x) +c* (x^2)参数:估计Std。误差t值Pr 2.129555 0.003976 535.56 <2e-16 **b -0.939467 0.018500 -50.78 <2e-16 **c -1.175413 0.017818 -65.97 <2e-16 *-符号。代码:0‘*’0.001‘*’0.01‘*’0.05‘.’0.1‘’1残差标准误差: 0.5114在105597自由度上迭代到收敛:1达到收敛容限: 2.58e-08

我还运行了一段代码来获得一些模型评估：

RSS <- sum(residuals(m)^2)
TSS <- sum((y - mean(y))^2)
R.square <- 1 - (RSS/TSS)

结果：

R.square 0.6365729

我不知道我的手术是否正统。我想知道我是否采取了正确的步骤。我也欣赏一些线索，知道什么是最好的方式来解释统计和报告这些结果。