与复合对象的圆碰撞
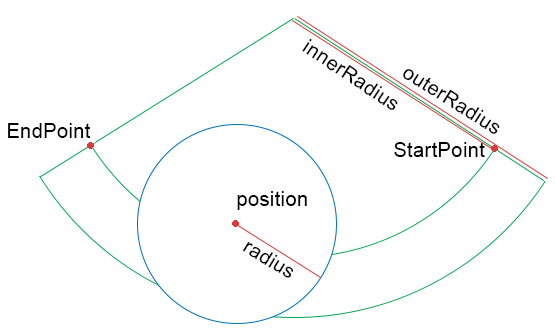
我想做一个圆环和圆环截面之间的碰撞检测。圆是由它的position位置和radius定义的。另一个对象由inner和outer半径定义,然后是startPoint和endPoint,两者都是x,y点。
在下面的例子中,this是圆,other是环部分。
首先,我只检查它是否与整个环碰撞。这是没有问题的。
float mag = this.position.Magnitude();
if (mag < other.InnerRadius() - this.radius ||
mag > other.OuterRadius() + this.radius) {
return false;
}但是,我需要检查圆是在这两个点定义的部分的内部还是外部。我能得到的最接近的,是检查它是否与开始向量和结束向量发生碰撞,但是当圆环完全在环段内时,这会返回错误的结果。
auto dot1 = Vector::Dot(position, other.StartPoint());
auto projected1 = dot1 / Vector::Dot(other.StartPoint(), other.StartPoint()) * other.StartPoint();
auto distance1 = Vector::Distance(position, projected1);
auto dot2 = Vector::Dot(position, other.EndPoint());
auto projected2 = dot2 / Vector::Dot(other.EndPoint(), other.EndPoint()) * other.EndPoint();
auto distance2 = Vector::Distance(position, projected2);
return distance1 < radius || distance2 < radius;检查一个圆是否与这两个向量定义的对象碰撞的最简单的方法是什么?
编辑:我在这里使用的所有点对象都是实现了所有向量操作的自定义Vector类。
Edit2:只是为了澄清一下,ring对象的原点是0,0
回答 2
Stack Overflow用户
发布于 2018-04-14 15:04:57
下面是一个简单的算法。
首先,让我们就变量名称达成一致:
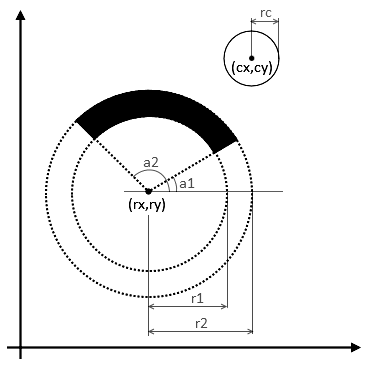
这里是r1 ≤ r2,-π/2 ≤ a1 ≤ a2 ≤ π/2。
(正如我在评论中被提醒的那样,你有起点和终点,而不是角度,但我会使用角度,因为它们看起来更方便。您可以通过atan2(y-ry, x-rx)轻松地从点获得角度,只需确保a1 ≤ a2。或者你可以重写算法,完全不使用角度。)
我们需要考虑三个不同的案例。这种情况取决于圆心相对于环段的位置:
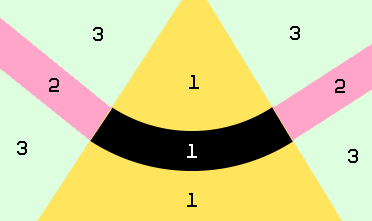
在第一种情况下,正如您已经指出的,如果向量(cx-rx, cy-ry)的长度大于r1-rc而小于r2+rc,则会发生碰撞。
在第二种情况下,如果圆心与最接近的直线边缘之间的距离小于rc,则发生碰撞。
在第三种情况下,如果圆心与4个拐角的最近距离小于rc,则发生碰撞。
以下是一些伪码:
rpos = vec2(rx,ry); // Ring segment center coordinates
cpos = vec2(cx,cy); // Circle coordinates
a = atan2(cy-ry, cx-rx); // Relative angle
r = length(cpos - rpos); // Distance between centers
if (a > a1 && a < a2) // Case 1
{
does_collide = (r+rc > a1 && r-rc < a2);
}
else
{
// Ring segment corners:
p11 = vec2(cos(a1), sin(a1)) * r1;
p12 = vec2(cos(a1), sin(a1)) * r2;
p21 = vec2(cos(a2), sin(a2)) * r1;
p22 = vec2(cos(a2), sin(a2)) * r2;
if (((cpos-p11) · (p12-p11) > 0 && (cpos-p12) · (p11-p12) > 0) ||
((cpos-p21) · (p22-p21) > 0 && (cpos-p22) · (p21-p22) > 0)) // Case 2
{
// Normals of straight edges:
n1 = normalize(vec2(p12.y - p11.y, p11.x - p12.x));
n2 = normalize(vec2(p21.y - p22.y, p22.x - p21.x));
// Distances to edges:
d1 = n1 · (cpos - p11);
d2 = n2 · (cpos - p21);
does_collide = (min(d1, d2) < rc);
}
else // Case 3
{
// Squared distances to corners
c1 = length_sqr(cpos-p11);
c2 = length_sqr(cpos-p12);
c3 = length_sqr(cpos-p21);
c4 = length_sqr(cpos-p22);
does_collide = (sqrt(min(c1, c2, c3, c4)) < rc);
}
}Stack Overflow用户
发布于 2018-04-14 14:47:44
要将小圆圈比作射线:
首先检查圆是否包含原点;如果是,则与射线相交。否则,继续读下去。
考虑从原点到圆心的向量v。规范它,规范射线R,取交叉乘积Rxv。如果它是正的,v是从R逆时针方向的,否则它是顺时针方向的,不管是从哪个方向,取acos来得到它们之间的角度。
如果圆有半径r,其中心距离原点d,则圆的角半宽(从原点看)等于(r/d)。如果R与v之间的夹角小于这一点,则圆与射线相交。
假设您知道对象是顺时针方向扩展,还是逆时针方向从头到尾扩展。(这些数字不会告诉你,你必须已经知道了,否则问题是无法解决的。)在你的例子中,它是顺时针方向的。现在,您必须小心;如果弧的角长度是<=π,那么您可以继续,否则就更容易确定圆是否在物体扇区之外的较小扇区。但假设物体的跨度较小,圆圈位于物体的扇区内(即射线之间)当且仅当它从一开始顺时针,从末端逆时针方向。
https://stackoverflow.com/questions/49832150
复制相似问题

