迭代平方时间复杂度
我有以下迭代平方的实现:
def power(a, b):
result = 1
while b > 0:
if b % 2 == 1:
result = mult(result, a)
a = mult(a, a)
b = b // 2
return resultmult()方法乘以2个给定的数,当一个是x比特的长度,另一个是y位的长度时,乘法所需的运算数是x*y+(x+y)运算,这在复杂性分析中需要考虑。
当a是n位长,b是m位长时,我试图找到一个O()表示法界,当a是n位长,b是m位长时,作为n和m函数完成的广义运算数的界。我只需要考虑乘法线,并检查最坏的情况。
最糟糕的情况是,当b是一个m位数时,所有m二进制数都是1,那么我就有循环的m迭代,在每一次迭代中,if条件都是真的。
我不知道该如何做,我应该如何在计算中考虑到a在每次迭代中都会增长?我如何把它用某种有限和,可能是几何级数,来计算呢?
谢谢
回答 3
Stack Overflow用户
发布于 2018-04-28 12:01:02
另外,我知道,乘以2位x位和y位会导致x*y+(x+y)异常操作。
这(一般)不是真的。一个处理器将在一个确定的循环数中将两个数字相乘,无论它们是否大。除非你是处理巨大的数字,你应该考虑,关于渐近复杂性(O),乘法作为一个运算,同样适用于加法,除法,.
在您的代码中,每个循环迭代有三个操作(if b % 2 == 1,可能是result = result*a,a = a*a,b = b // 2)。复杂性仅取决于循环的迭代次数,即: log2(b),因为b在每次迭代中被除以两次。
对于庞大的数字,您有两个操作可能会对渐近复杂性产生影响:result = result*a和a = a*a。Cpython使用Karatsuba增殖,如果n是数字的数字数,则为O(n^log2 2(3))。
我只想详细介绍一下a*a。当你取一个数字的平方,你大概把数字的数目乘以二。考虑log2(b)循环:a*a在第一次迭代中取O(n^log2 2(3)),在第二次迭代中取O(2n^log2 2(3)),在第二迭代中取O(4N^log2 2(3)),在最后一次迭代中取O(Bn)^log2 2(3)。之和是O(b*log2 2(B)*n)^log2 2(3),如果我没有错的话!
对于a*a,如果您被绑定到O(x*y)乘法算法,那么对于您的log2(b)循环,
- 第一次迭代的O(n^2);
- 第二次迭代的O(2n)^2;
- 第三次迭代O((4n)^2);
- K次迭代的O(2^(k-1)*n)^2.
这是O(b^2 * n^2) = O(2^2m * n^2),我认为(现在没有时间检查!)。
Stack Overflow用户
发布于 2018-04-28 11:12:34
我认为这种算法的复杂性与a无关。
在回顾复杂性时,我认为循环数是由于m而导致的最高复杂度的主要指标。
在b的值中运行,如果b>0时,我们可以看到如下数字:
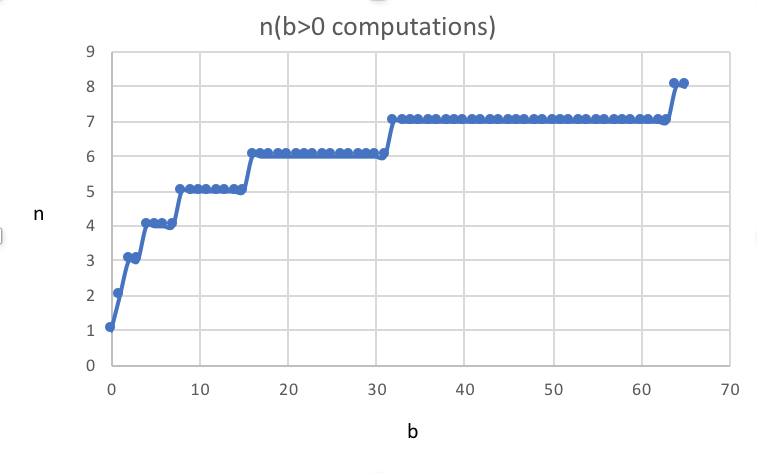
有趣的是,我们看到每个2的倍数(即1,2,4,8,16,32,64)的n个循环的增加。
粗略地说,我认为这个算法的复杂性与O(log2(n))密切相关。
Stack Overflow用户
发布于 2018-04-28 13:01:22
嗯,经过一些分析,我认为power方法的迭代次数将在2^(2i-1)*n+(2^(i-1)+2^i*n+(2^i*n)^2+2^(i+1)*n的i(从0到m-1)上求和,并且得到复杂度:O(4^m*n^2)是非常直接的。
https://stackoverflow.com/questions/50075509
复制相似问题

