问动态规划:我有重叠子问题吗？

EN

我的算法

假设我有一个二维的实数数组。我从这个数组中的一个特定的单元格开始，其中包含一个特别大的数字。我想标记其他单元格中的哪个应该属于上述开始单元格。规则是这样的:如果我找到了从开始单元格到另一个单元格的步行方式，则另一个单元格属于开始单元格。我只能在牢房里上下走动。我只能从一个数字较高的牢房走到一个号码较低的牢房。下面是我从中心9开始的一个例子

​

​

我的伪算法是

function Step(cellNr):
    foreach neighborNr in neighbors_of(cellNr):
        if array_value(neighborNr) < array_value(cellNr):
            mark_cell(neighborNr)
            Step(neighborNr)
Step(centerNr)

现在来了第二个方面，我不仅对一个开始单元格，而且对多个开始单元格都这样做。

​

​

动态规划

我研究了动态规划，发现为了能够应用动态规划，需要满足两个条件：

• 子问题需要重叠
• 子问题需要有最优的子结构

“动态规划是指以递归的方式将复杂的问题分解成简单的子问题.如果一个问题可以通过把它分解成子问题，然后递归地找到子问题的最优解来解决，那么它就被称为有最优子结构。..。要使动态规划适用，一个问题必须具备两个关键属性:最优子结构和重叠子问题。如果一个问题可以通过组合不重叠子问题的最优解来解决，那么这种策略被称为“分而治之”。这就是合并排序和快速排序不被归类为动态规划问题的原因。最优子结构是指通过优化子问题的最优解的组合，得到给定优化问题的解。这种最优子结构通常用递归来描述。..。重叠子问题意味着子问题的空间必须很小，也就是说，任何递归算法解决问题都应该一次又一次地解决相同的子问题，而不是产生新的子问题。“维基百科。

我想知道我的算法是否是动态规划。它绝对是递归的，并且在子结构上似乎是最优的。不过，我开始对重叠的子结构感到好奇了。有一个关于Fibonacci数的例子，但在我看来，关键方面是可以存储递归算法的中间结果。对于我的算法，中间结果不能存储--至少不能存储单个开始单元的一次运行。然而，当我考虑整个问题时，由于有许多起始单元格，我们发现其中一些区域是相互关联的：

​

​

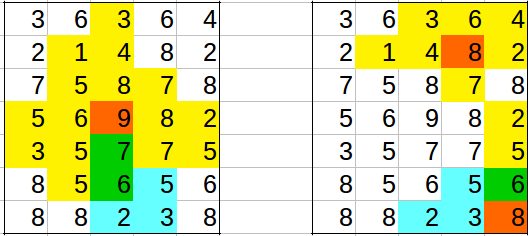
让我们从左边图像中的橙色9开始，沿着绿色的路径一直走到蓝色的5。从这里我们也可以得到蓝色3和蓝色2。我们完成了左边橙色9的算法。

现在我们转到右图中的下橙色8。我们从这8开始，沿着绿色的路径走到绿色的6。从这里我们得到蓝色的5。我们已经从先前的计算中知道(从左边图像中的橙色9)，蓝色3和蓝色2是可以从蓝色5到达的，所以我们可以一举标记它们，而不需要重新计算路径。

这就是为什么我认为我的整体问题是可以用动态规划解决的。

问题

1. 我的算法/问题是动态规划吗？为什么为什么不呢？
2. 如果不是，我能把它变成动态规划吗?如果是的话，怎么做？