用Runge-Kutta-4方法模拟Python (物理)中的轨道
用Runge-Kutta-4方法模拟Python (物理)中的轨道
提问于 2018-11-04 13:51:34
我正在尝试实现一种RK4方法来求解绕地球的火箭轨道。最终,这段代码将被用于更复杂的太阳系模拟,但我只是想让它首先在这个简单的系统中工作。我的代码在下面-我希望有人能告诉我它有什么问题。我解决问题的努力很长时间也没有结果,但我要总结一下我的发现:
- 我相信加速功能是正确的,因为它给出可信的数值,并符合我的计算器/大脑。
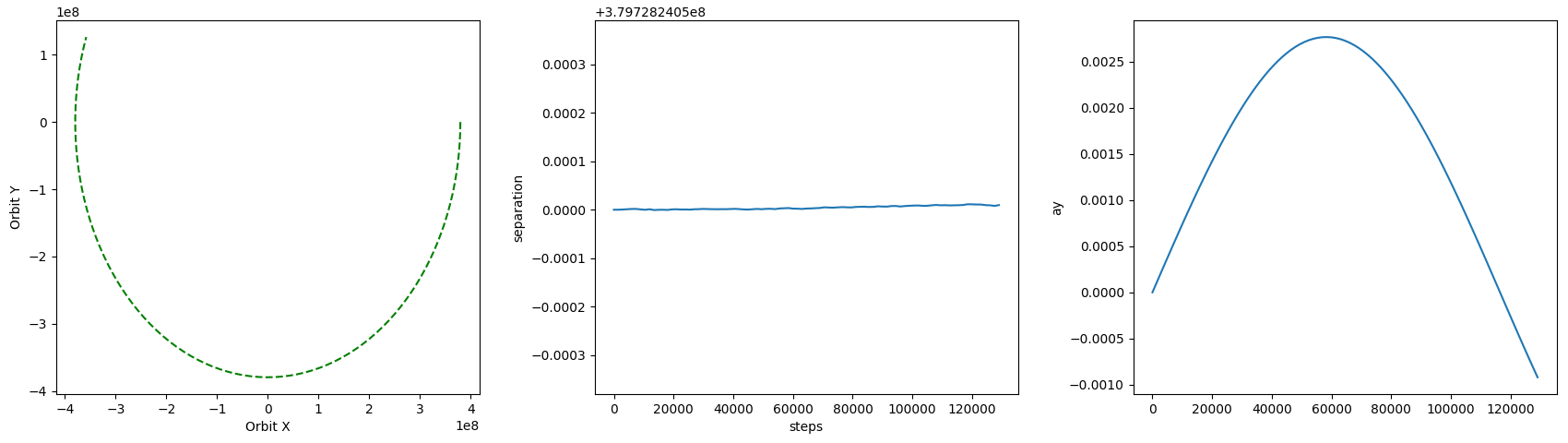
- 似乎问题就在计算下一个"r“值的某个地方--当你运行这段代码时,会出现一个x-y图,显示火箭最初落在地球上,然后又反弹,然后返回。在这一点上,我打印了所有相关的值,发现"v“和"a”在两个组件中都是负值,尽管火箭明显地朝正y方向移动。这使我认为新的"r“的计算与物理学不符。
- 火箭落到地球的速度比它应该的速度快得多,这也是可疑的(从技术上讲,它根本不应该落入地球,因为初始速度被设定为所需的轨道速度)
无论哪种方式,如果有人能发现错误,我会非常感激,因为我一直无法做到这一点。
from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
mE = 5.9742e24 #earth mass
mM = 7.35e22 #moon mass
dM = 379728240.5 #distance from moon to barycentre
dE = 4671759.5 #distance from earth to barycentre
s = 6.4686973e7 #hypothesised distance from moon to Lagrange-2 point
sr = 6.5420e7 #alternate L2 distance
def Simulate(iterations):
x = dM #initialise rocket positions
y = 0
a = 10 #set the time step
xdot = 0. #initialise rocket velocity
ydot = -((6.6726e-11)*mE/x)**0.5
rocket_history_x, rocket_history_y = [[] for _ in range(2)]
history_mx, history_my = [[] for _ in range(2)]
history_ex, history_ey = [[] for _ in range(2)]
sep_history, step_history = [[] for _ in range(2)] #create lists to store data in
history_vx, history_vy = [[] for _ in range(2)]
history_ax, history_ay = [[] for _ in range(2)]
n = 1500
m = 10000 #n,m,p are for storing every nth, mth and pth value to the lists
p = 60000
r = np.array((x,y)) #create rocket position vector
v = np.array((xdot, ydot)) #create rocket velocity vector
for i in range(iterations):
xe, ye = 0, 0 #position of earth
re = np.array((xe,ye)) #create earth position vector
phi = np.arctan2((r[1]-ye),(r[0]-xe)) #calculate phi, the angle between the rocket and the earth, as measured from the earth
r_hat_e = np.array((np.cos(phi), np.sin(phi))) #create vector along which earth's acceleration acts
def acc(r): #define the acceleration vector function
return ((-6.6726e-11)*(mE)/abs(np.dot((r-re),(r-re))))*r_hat_e
k1v = acc(r) #use RK4 method
k1r = v
k2v = acc(r + k1r*(a/2)) #acc(r + (a/2)*v)
k2r = v * (a/2) * k1v # v*acc(r)
k3v = acc(r + k2r*(a/2)) #acc(r + (a/2)*v*acc(r))
k3r = v * k2v * (a/2) #v*(a/2)*acc(r + (a/2)*v)
k4v = acc(r + k3r*a) #acc(r + (a**2/2)*v*acc(r + (a/2)*v))
k4r = v * k3v * a #v*a*acc(r + (a/2)*v*acc(r))
v = v + (a/6) * (k1v + 2*k2v + 2*k3v + k4v) #update v
r = r + (a/6) * (k1r + 2*k2r + 2*k3r + k4r) #update r
sep = np.sqrt(np.dot((r-re),(r-re))) #separation of rocket and earth, useful for visualisation/trouble-shooting
if i% n == 0: # Check for the step
rocket_history_x.append(r[0])
rocket_history_y.append(r[1])
history_ex.append(xe)
history_ey.append(ye)
sep_history.append(sep) #putting data into lists for plotting and troubleshooting
step_history.append(i)
history_ax.append(acc(r)[0])
history_ay.append(acc(r)[1])
history_vx.append(v[0])
history_vy.append(v[1])
#if i% m == 0: # Check for the step
#print r
#print acc(r)
#if i% p == 0: # Check for the step
#print ((a/6)*(k1v + 2*k2v + 2*k3v + k4v))
#print ((a/6)*(k1r + 2*k2r + 2*k3r + k4r))
#print k1v, k2v, k3v, k4v
#print k1r, k2r, k3r, k4r
return rocket_history_x, rocket_history_y, history_ex, history_ey, history_mx, history_my, sep_history, step_history, history_ax, history_ay, history_vx, history_vy
x , y, xe, ye, mx, my, sep, step, ax, ay, vx, vy = Simulate(130000)
#print x,y,vx,vy,ax,ay,step
print ("Plotting graph...")
plt.figure()
plt.subplot(311)
plt.plot(x, y, linestyle='--', color = 'green')
#plt.plot(mx, my, linestyle='-', color = 'blue')
plt.plot(xe, ye, linestyle='-', color = 'red')
#plt.plot(xm, ym)
plt.xlabel("Orbit X")
plt.ylabel("Orbit Y")
'''
plt.plot(step, vy)
plt.ylabel("vy")
'''
plt.subplot(312)
plt.plot(step, sep)
plt.xlabel("steps")
plt.ylabel("separation")
plt.subplot(313)
plt.plot(step, ay)
plt.ylabel("ay")
plt.show()
print("Simulation Complete")回答 1
Stack Overflow用户
回答已采纳
发布于 2018-11-04 15:25:00
您最严重的错误是在计算v斜率时,您使用乘法而不是加法。
k1v = acc(r) #use RK4 method
k1r = v
k2v = acc(r + (a/2) * k1r)
k2r = v + (a/2) * k1v
k3v = acc(r + (a/2) * k2r)
k3r = v + (a/2) * k2v
k4v = acc(r + a * k3r)
k4r = v + a * k3v 第二个错误是在加速计算更改状态时使用来自不同状态的值。这可能会将方法的顺序降到1,这可能不会明显地改变这个图,但是在较长的集成周期内会有更大的错误。使用
def acc(r): #define the acceleration vector function
return ((-6.6726e-11)*(mE)/abs(np.dot((r-re),(r-re)))**1.5)*(r-re)
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/53141542
复制相关文章
相似问题

