用6表示python中的循环累积和
数学问题是:
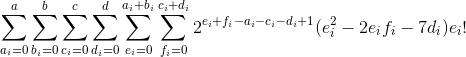
和内的表达式实际上比上面的要复杂得多,但这是为了一个最小的工作例子,以避免过于复杂的事情。我用Python编写了这篇文章,使用了6个嵌套的for循环,正如预期的那样,它执行得非常糟糕(真正的表单执行得很糟糕,需要评估数百万次),甚至在Numba、Cython和朋友的帮助下也是如此。在这里,它使用嵌套的for循环和累积和编写:
import numpy as np
def func1(a,b,c,d):
'''
Minimal working example of multiple summation
'''
B = 0
for ai in range(0,a):
for bi in range(0,b):
for ci in range(0,c):
for di in range(0,d):
for ei in range(0,ai+bi):
for fi in range(0,ci+di):
B += (2)**(ei-fi-ai-ci-di+1)*(ei**2-2*(ei*fi)-7*di)*np.math.factorial(ei)
return a, b, c, d, B表达式以4个数字作为输入,对于func1(4,6,3,4),B的输出为21769947.844726562。
我四处寻找这方面的帮助,并找到了几个Stack帖子,其中一些例子如下:
Exterior product in NumPy : Vectorizing six nested loops
Vectorizing triple for loop in Python/Numpy with different array shapes
Python vectorizing nested for loops
我试着用我从这些有用的帖子中学到的东西,但经过多次尝试,我总是得出错误的答案。即使是向量化的一个内部和将获得一个巨大的性能收益,为真正的问题,但事实是,和范围是不同的,似乎是让我放弃。有没有人对如何在这方面取得进展有任何建议?
回答 4
Stack Overflow用户
发布于 2018-11-14 17:44:16
编辑3:
最后(我认为)版本,更干净和更快地融合了来自max9111's answer的想法。
import numpy as np
from numba import as nb
@nb.njit()
def func1_jit(a, b, c, d):
# Precompute
exp_min = 5 - (a + b + c + d)
exp_max = b
exp = 2. ** np.arange(exp_min, exp_max + 1)
fact_e = np.empty((a + b - 2))
fact_e[0] = 1
for ei in range(1, len(fact_e)):
fact_e[ei] = ei * fact_e[ei - 1]
# Loops
B = 0
for ai in range(0, a):
for bi in range(0, b):
for ci in range(0, c):
for di in range(0, d):
for ei in range(0, ai + bi):
for fi in range(0, ci + di):
B += exp[ei - fi - ai - ci - di + 1 - exp_min] * (ei * ei - 2 * (ei * fi) - 7 * di) * fact_e[ei]
return B这已经比前面的任何选项快得多了,但是我们仍然没有利用多个CPU。这样做的一种方法是在函数本身内,例如并行化外部循环。这在每次调用创建线程时都会增加一些开销,因此对于较小的输入实际上要慢一些,但是对于更大的值,则应该要快得多:
import numpy as np
from numba import as nb
@nb.njit(parallel=True)
def func1_par(a, b, c, d):
# Precompute
exp_min = 5 - (a + b + c + d)
exp_max = b
exp = 2. ** np.arange(exp_min, exp_max + 1)
fact_e = np.empty((a + b - 2))
fact_e[0] = 1
for ei in range(1, len(fact_e)):
fact_e[ei] = ei * fact_e[ei - 1]
# Loops
B = np.empty((a,))
for ai in nb.prange(0, a):
Bi = 0
for bi in range(0, b):
for ci in range(0, c):
for di in range(0, d):
for ei in range(0, ai + bi):
for fi in range(0, ci + di):
Bi += exp[ei - fi - ai - ci - di + 1 - exp_min] * (ei * ei - 2 * (ei * fi) - 7 * di) * fact_e[ei]
B[ai] = Bi
return np.sum(B)或者,如果您有许多要计算函数的点,您也可以在该级别并行化。在这里,a_arr、b_arr、c_arr和d_arr是要计算函数的值向量:
from numba import as nb
@nb.njit(parallel=True)
def func1_arr(a_arr, b_arr, c_arr, d_arr):
B_arr = np.empty((len(a_arr),))
for i in nb.prange(len(B_arr)):
B_arr[i] = func1_jit(a_arr[i], b_arr[i], c_arr[i], d_arr[i])
return B_arr最佳配置取决于您的输入、使用模式、硬件等,因此您可以结合不同的想法来适应您的情况。
编辑2:
事实上,忘了我之前说过的话。最好的方法是JIT-编译算法,但以一种更有效的方式。首先计算昂贵的部分(我取了指数和阶乘),然后将其传递给已编译的循环函数:
import numpy as np
from numba import njit
def func1(a, b, c, d):
exp_min = 5 - (a + b + c + d)
exp_max = b
exp = 2. ** np.arange(exp_min, exp_max + 1)
ee = np.arange(a + b - 2)
fact_e = scipy.special.factorial(ee)
return func1_inner(a, b, c, d, exp_min, exp, fact_e)
@njit()
def func1_inner(a, b, c, d, exp_min, exp, fact_e):
B = 0
for ai in range(0, a):
for bi in range(0, b):
for ci in range(0, c):
for di in range(0, d):
for ei in range(0, ai + bi):
for fi in range(0, ci + di):
B += exp[ei - fi - ai - ci - di + 1 - exp_min] * (ei * ei - 2 * (ei * fi) - 7 * di) * fact_e[ei]
return B在我的实验中,这是目前为止最快的选择,几乎不需要额外的内存(只有预先计算出来的值,输入的大小是线性的)。
a, b, c, d = 4, 6, 3, 4
# The original function
%timeit func1_orig(a, b, c, d)
# 2.07 ms ± 33.7 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
# The grid-evaluated function
%timeit func1_grid(a, b, c, d)
# 256 µs ± 25 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
# The precompuation + JIT-compiled function
%timeit func1_jit(a, b, c, d)
# 19.6 µs ± 3.25 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each)好吧,总有网格的选择--评估整个事情:
import numpy as np
import scipy.special
def func1(a, b, c, d):
ai, bi, ci, di, ei, fi = np.ogrid[:a, :b, :c, :d, :a + b - 2, :c + d - 2]
# Compute
B = (2.) ** (ei - fi - ai - ci - di + 1) * (ei ** 2 - 2 * (ei * fi) - 7 * di) * scipy.special.factorial(ei)
# Mask out of range elements for last two inner loops
m = (ei < ai + bi) & (fi < ci + di)
return np.sum(B * m)
print(func1(4, 6, 3, 4))
# 21769947.844726562我使用scipy.special.factorial是因为显然由于某种原因,np.factorial无法处理数组。
很明显,随着参数的增加,内存成本会增长得很快。实际上,代码执行的计算比所需的要多,因为两个内部循环的迭代次数不同,所以(在这种方法中)您必须使用最大的,然后删除不需要的内容。希望矢量化能弥补这一点。一个小的IPython基准:
a, b, c, d = 4, 6, 3, 4
# func1_orig is the original loop-based version
%timeit func1_orig(a, b, c, d)
# 2.9 ms ± 110 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
# func1 here is the vectorized version
%timeit func1(a, b, c, d)
# 210 µs ± 6.34 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)编辑:
注意,前面的方法也不是什么都没有的。您可以选择网格-只计算一些循环。例如,两个最内部的循环可以像这样进行矢量化:
def func1(a, b, c, d):
B = 0
e = np.arange(a + b - 2).reshape((-1, 1))
f = np.arange(c + d - 2)
for ai in range(0, a):
for bi in range(0, b):
ei = e[:ai + bi]
for ci in range(0, c):
for di in range(0, d):
fi = f[:ci + di]
B += np.sum((2.) ** (ei - fi - ai - ci - di + 1) * (ei ** 2 - 2 * (ei * fi) - 7 * di) * scipy.special.factorial(ei))
return B这仍然有循环,但它确实避免了额外的计算,并且内存需求要低得多。哪个是最好的取决于输入的大小,我猜。在我的测试中,对于原始值(4、6、3、4),这甚至比原来的函数还要慢;而且,对于这种情况,在每个循环中为ei和fi创建新的数组似乎比在预先创建的一个片段上操作更快。但是,如果将输入乘以4 (14、24、12、16),那么这比原始输入(关于x5)要快得多,尽管比完全向量化的输入(关于x3)慢得多。另一方面,我可以用这个值(在5分钟内)计算10 (40、60、30、40)的输入值,但由于内存(我没有测试原始函数所用的时间),而不能计算前一个输入的值。使用@numba.jit有点帮助,虽然不是很大(由于阶乘函数不能使用nopython )。根据输入的大小,您可以尝试或多或少地对循环进行矢量化。
Stack Overflow用户
发布于 2018-11-15 13:10:20
这只是对@jdehesa回答的一个评论。
如果Numba本身不支持某个函数,那么通常建议自己实现它。在分解的情况下,这并不是一项复杂的任务。
码
import numpy as np
import numba as nb
@nb.njit()
def factorial(a):
res=1.
for i in range(1,a+1):
res*=i
return res
@nb.njit()
def func1(a, b, c, d):
B = 0.
exp_min = 5 - (a + b + c + d)
exp_max = b
exp = 2. ** np.arange(exp_min, exp_max + 1)
fact_e=np.empty(a + b - 2)
for i in range(a + b - 2):
fact_e[i]=factorial(i)
for ai in range(0, a):
for bi in range(0, b):
for ci in range(0, c):
for di in range(0, d):
for ei in range(0, ai + bi):
for fi in range(0, ci + di):
B += exp[ei - fi - ai - ci - di + 1 - exp_min] * (ei * ei - 2 * (ei * fi) - 7 * di) * fact_e[ei]
return B并行版本
@nb.njit(parallel=True)
def func_p(a_vec,b_vec,c_vec,d_vec):
res=np.empty(a_vec.shape[0])
for i in nb.prange(a_vec.shape[0]):
res[i]=func1(a_vec[i], b_vec[i], c_vec[i], d_vec[i])
return res示例
a_vec=np.random.randint(low=2,high=10,size=1000000)
b_vec=np.random.randint(low=2,high=10,size=1000000)
c_vec=np.random.randint(low=2,high=10,size=1000000)
d_vec=np.random.randint(low=2,high=10,size=1000000)
res_2=func_p(a_vec,b_vec,c_vec,d_vec)单线程版本将导致示例中的5.6的(在第一次运行之后)。
并行版本几乎会导致计算许多值的另一个Number_of_Cores加速比。请记住,并行版本的编译开销更大(对于第一次调用,编译开销超过0.5s )。
Stack Overflow用户
发布于 2018-11-14 17:58:20
使用这个product函数,您可以将嵌套的循环转换为矩阵,然后您可以简单地以矢量化的方式计算各自的嵌套西格玛:
In [37]: def nested_sig(args):
...: base_prod = cartesian_product(*arrays)
...: second_prod = cartesian_product(base_prod[:,:2].sum(1), base_prod[:,2:].sum(1))
...: total = np.column_stack((base_prod, second_prod))
...: # the items in each row denotes the following variables in order:
...: # ai, bi, ci, di, ei, fi
...: x = total[:, 4] - total[:, 5] - total[:, 0] - total[:, 2] - total[:, 3] + 1
...: y = total[:, 4] - total[:, 5]
...: result = np.power(2, x) * (np.power(total[:, 4], 2) - 2*y - 7*total[:, 3]) * np.math.factorial(total[:,4])
...: return resulthttps://stackoverflow.com/questions/53305490
复制相似问题

