渐近方程(python)中的未知数学误差
渐近方程(python)中的未知数学误差
提问于 2018-11-26 13:34:45
我试图在r(0,20)范围内绘制函数j0、j1和j10,方法是使用lambdify将函数转换为numpy格式。我使用了以下代码:
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym
from ipywidgets.widgets import interact
sym.init_printing(use_latex="mathjax")
x, y, z, t = sym.symbols('x y z t')
r = sym.symbols("r", positive=True)
j0 = (sym.diff(((sym.cos(sym.sqrt(r**2-2*r*t)))/r),t)).subs({t:0})
j1 = (sym.diff(((sym.cos(sym.sqrt(r**2-2*r*t)))/r),t,2)).subs({t:0})
j10 = (sym.diff(((sym.cos(sym.sqrt(r**2-2*r*t)))/r),t,11)).subs({t:0})
k = sym.lambdify(r,j0)
l = sym.lambdify(r,j1)
m = sym.lambdify(r,j10)
myr = np.linspace(0,20,1000)
plt.plot(myr,k(myr),label="$j_{0}(r)$")
plt.plot(myr,l(myr),label="$j_{1}(r)$")
plt.plot(myr,m(myr),label="$j_{10}(r)$")
plt.ylim(-1,1)
plt.legend()
plt.xlabel("r")
plt.ylabel("$j_{n}(r)$")我得到了这个输出:
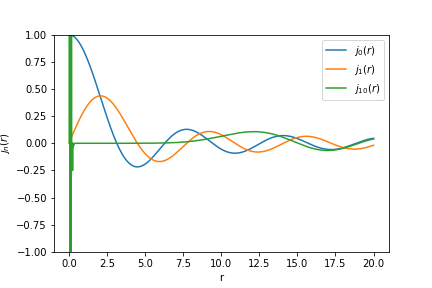
这似乎至少在一定程度上是正确的,但是我也收到了一条我从未见过的错误消息:
/anaconda3/lib/python3.6/site-packages/numpy/__init__.py:1: RuntimeWarning: invalid value encountered in true_divide
"""
/anaconda3/lib/python3.6/site-packages/numpy/__init__.py:1: RuntimeWarning: invalid value encountered in true_divide
"""
/anaconda3/lib/python3.6/site-packages/numpy/__init__.py:1: RuntimeWarning: divide by zero encountered in true_divide
"""
/anaconda3/lib/python3.6/site-packages/numpy/__init__.py:1: RuntimeWarning: invalid value encountered in true_divide
"""
/anaconda3/lib/python3.6/site-packages/numpy/__init__.py:1: RuntimeWarning: divide by zero encountered in true_divide
"""我怀疑这与使用.subs({t:0})有关,但是,经过大量修改和重新处理代码后,我发现如果不使用.subs,就无法获得j0、j1和j10所需的公式。我认为,当我试图将j10的公式替换为以下公式(应该为0)时,这个错误会产生连锁效应,因为我引用了“不正确的语法”:
(r**2)*sym.diff(m,r,2) + (2*r)*sym.diff(m,r) + (r**2 - 10*(10+1))*m其中m是j10的numpy版本。
任何帮助都将不胜感激。
回答 1
Stack Overflow用户
回答已采纳
发布于 2018-11-27 06:19:39
您的问题是由除以零引起的,这在数值上是很难处理的,尽管r->0的极限可能是有限的。对于这个问题,我有两种(稍微不同的)解决方案。
1)用数学精确结果代替问题点。在您的示例中,这将意味着类似的内容(limit是您首先从纸上导出的r->0函数的精确解):
myr = np.linspace(0,20,1000)
k_noerror = np.concatenate([[limit], k(myr[1:])])
plt.plot(myr,k_noerror,label="$j_{0}(r)$")2)如果你不能自己计算极限,你可以用一个很小的值来代替你的零,即:
myr = np.linspace(0,20,1000)
myr[0] = 1e-3
plt.plot(myr,k(myr),label="$j_{0}(r)$")页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/53482281
复制相关文章
相似问题

