线性回归中StandardScaler与正规化器结果的比较
我正在研究不同场景下线性回归的一些例子,比较使用Normalizer和StandardScaler的结果,结果令人费解。
我正在使用波士顿住房数据集,并以这样的方式准备:
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
#load the data
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df['PRICE'] = boston.target目前,我正试图对从以下场景中得到的结果进行推理:
- 用参数
normalize=True和Normalizer初始化线性回归 - 用参数
fit_intercept = False初始化线性回归,不论标准化与否。
总的来说,我觉得结果令人困惑。
我是这样安排一切的:
# Prep the data
X = df.iloc[:, :-1]
y = df.iloc[:, -1:]
normal_X = Normalizer().fit_transform(X)
scaled_X = StandardScaler().fit_transform(X)
#now prepare some of the models
reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)
reg3 = LinearRegression().fit(normal_X, y)
reg4 = LinearRegression().fit(scaled_X, y)
reg5 = LinearRegression(fit_intercept=False).fit(scaled_X, y)然后,我创建了三个单独的数据框架来比较每个模型的R_score、系数值和预测值。
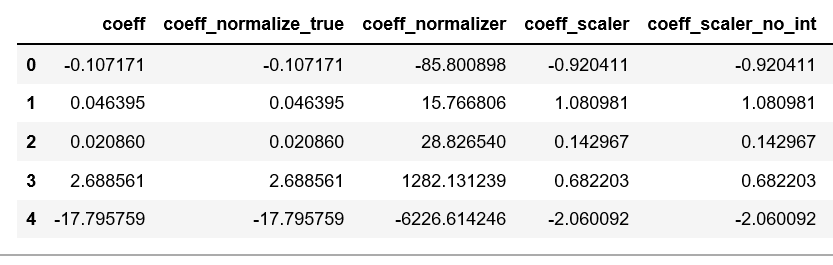
为了创建用于比较每个模型的系数值的数据,我执行了以下操作:
#Create a dataframe of the coefficients
coef = pd.DataFrame({
'coeff': reg1.coef_[0],
'coeff_normalize_true': reg2.coef_[0],
'coeff_normalizer': reg3.coef_[0],
'coeff_scaler': reg4.coef_[0],
'coeff_scaler_no_int': reg5.coef_[0]
})下面是我如何创建dataframe来比较每个模型的R^2值:
scores = pd.DataFrame({
'score': reg1.score(X, y),
'score_normalize_true': reg2.score(X, y),
'score_normalizer': reg3.score(normal_X, y),
'score_scaler': reg4.score(scaled_X, y),
'score_scaler_no_int': reg5.score(scaled_X, y)
}, index=range(1)
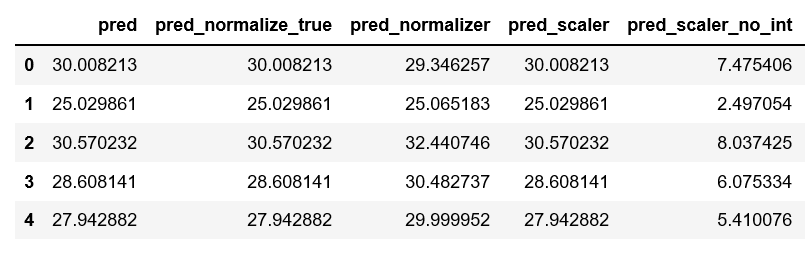
)最后,下面是比较每一种预测的数据:
predictions = pd.DataFrame({
'pred': reg1.predict(X).ravel(),
'pred_normalize_true': reg2.predict(X).ravel(),
'pred_normalizer': reg3.predict(normal_X).ravel(),
'pred_scaler': reg4.predict(scaled_X).ravel(),
'pred_scaler_no_int': reg5.predict(scaled_X).ravel()
}, index=range(len(y)))下面是生成的数据文件:
COEFFICIENTS:
分数:

PREDICTIONS:
我有三个我无法调和的问题:
- 为什么前两种模式完全没有区别?设置
normalize=False似乎没有任何作用。我能理解有相同的预测值和R^2值,但是我的特性有不同的数值尺度,所以我不知道为什么正常化会没有任何影响。当您考虑到使用StandardScaler会显着地改变系数时,这是双重混淆的。 - 我不明白为什么使用
Normalizer的模型会导致与其他模型完全不同的系数值,特别是当带有LinearRegression(normalize=True)的模型完全没有变化的时候。
如果要查看每个文档,它们似乎非常相似,如果不是完全相同的话。
规范化:布尔、可选、默认的假 当fit_intercept设置为False时,将忽略此参数。如果为真,则在回归之前,通过减去均值,再除以L2-范数,将回归量X归一化。
同时,sklearn.preprocessing.Normalizer 默认情况下,它将规范为l2规范。上的文档。
我看不出这两个选项之间有什么区别,我也不明白为什么其中一个在系数值上会与另一个有如此大的差别。
- 使用
StandardScaler的模型的结果对我来说是一致的,但是我不明白为什么使用StandardScaler和设置set_intercept=False的模型表现这么差。
从线性回归模上的文档
fit_intercept :布尔值,可选,默认的真 是否计算此模型的截距。如果设置为False,则不 拦截将用于计算(例如,数据预计已经被使用)。 中心)。
StandardScaler将您的数据作为中心,所以我不明白为什么将它与fit_intercept=False一起使用会产生不一致的结果。
回答 3
Stack Overflow用户
发布于 2019-01-10 15:02:36
- 前两个模型之间的系数没有差别的原因是,在从标准化输入数据计算出系数之后,
Sklearn对幕后的系数进行了去规范化。参考文献
这种去归一化是因为对于测试数据,我们可以直接应用协同效应.在不对测试数据进行规范化的情况下得到预测结果。
因此,设置normalize=True确实会对效率产生影响,但它们不会影响最佳匹配线。
Normalizer对每个样本进行规范化(意思是按行排列)。您可以看到引用代码这里。
将个别样本标准化为单位规范。
而normalize=True则针对每一列/特性进行规范化。参考文献
示例以了解规范化在数据的不同维度上的影响。让我们以二维x1 & x2和y作为目标变量。目标变量值在图中进行颜色编码。
import matplotlib.pyplot as plt
from sklearn.preprocessing import Normalizer,StandardScaler
from sklearn.preprocessing.data import normalize
n=50
x1 = np.random.normal(0, 2, size=n)
x2 = np.random.normal(0, 2, size=n)
noise = np.random.normal(0, 1, size=n)
y = 5 + 0.5*x1 + 2.5*x2 + noise
fig,ax=plt.subplots(1,4,figsize=(20,6))
ax[0].scatter(x1,x2,c=y)
ax[0].set_title('raw_data',size=15)
X = np.column_stack((x1,x2))
column_normalized=normalize(X, axis=0)
ax[1].scatter(column_normalized[:,0],column_normalized[:,1],c=y)
ax[1].set_title('column_normalized data',size=15)
row_normalized=Normalizer().fit_transform(X)
ax[2].scatter(row_normalized[:,0],row_normalized[:,1],c=y)
ax[2].set_title('row_normalized data',size=15)
standardized_data=StandardScaler().fit_transform(X)
ax[3].scatter(standardized_data[:,0],standardized_data[:,1],c=y)
ax[3].set_title('standardized data',size=15)
plt.subplots_adjust(left=0.3, bottom=None, right=0.9, top=None, wspace=0.3, hspace=None)
plt.show()
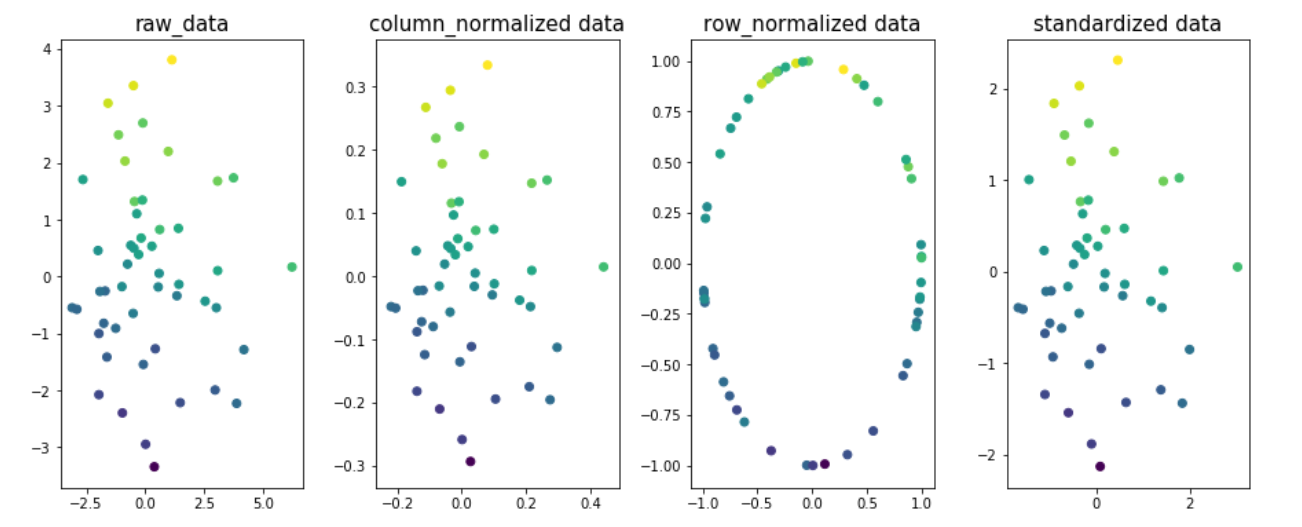
您可以看到,图1、2和4中数据的最佳匹配行是相同的;表示由于列/特性规范化或数据标准化,r2-得分不会改变。只是这样,结果却是不同的合作伙伴。值。
注:fig3的最佳适合线将有所不同。
- 当您设置fit_intercept=False时,偏差项将从预测中减去。这意味着拦截被设置为零,否则这将是目标变量的平均值。
对于目标变量没有缩放的问题(均值=0),拦截为零的预测应该执行不好的操作。您可以在每一行中看到22.532的差异,这意味着输出的影响。
Stack Overflow用户
发布于 2019-01-10 16:00:53
回答Q1
我假设前两个模型的意思是reg1和reg2。如果情况并非如此,请告诉我们。
如果您是否将数据规范化,线性回归具有相同的预测能力。因此,使用normalize=True对预测没有影响。了解这一点的一种方法是看到归一化(按列排列)是对每个列((x-a)/b)的线性运算,线性回归数据的线性转换不会影响系数估计,只会改变它们的值。请注意,对于Lasso/Ridge/ElasticNet,此语句不正确。
那么,为什么系数没有区别呢?normalize=True还考虑到用户通常想要的是原始特征上的系数,而不是标准化的特性。因此,它调整系数。检查这是否合理的一种方法是使用一个简单的示例:
# two features, normal distributed with sigma=10
x1 = np.random.normal(0, 10, size=100)
x2 = np.random.normal(0, 10, size=100)
# y is related to each of them plus some noise
y = 3 + 2*x1 + 1*x2 + np.random.normal(0, 1, size=100)
X = np.array([x1, x2]).T # X has two columns
reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)
# check that coefficients are the same and equal to [2,1]
np.testing.assert_allclose(reg1.coef_, reg2.coef_)
np.testing.assert_allclose(reg1.coef_, np.array([2, 1]), rtol=0.01)这两种方法都正确地捕捉了x1、x2和y之间的真实信号,即分别为2和1。
回答Q2
Normalizer不是你所期望的那样。它对每一行都进行了规范化。因此,结果将发生巨大的变化,并可能破坏功能与目标之间的关系,除了特定的情况(例如TF-国防军)。
要了解如何使用上述示例,请考虑另一个特性x3,它与y无关。使用Normalizer会使x1被x3的值所修改,从而降低它与y关系的强度。
模型之间系数的差异(1,2)和(4,5)
系数之间的差异在于,当你在拟合前标准化时,系数将相对于标准化的特征,也就是我在答案的第一部分中提到的系数。可以使用reg4.coef_ / scaler.scale_将它们映射到原始参数。
x1 = np.random.normal(0, 10, size=100)
x2 = np.random.normal(0, 10, size=100)
y = 3 + 2*x1 + 1*x2 + np.random.normal(0, 1, size=100)
X = np.array([x1, x2]).T
reg1 = LinearRegression().fit(X, y)
reg2 = LinearRegression(normalize=True).fit(X, y)
scaler = StandardScaler()
reg4 = LinearRegression().fit(scaler.fit_transform(X), y)
np.testing.assert_allclose(reg1.coef_, reg2.coef_)
np.testing.assert_allclose(reg1.coef_, np.array([2, 1]), rtol=0.01)
# here
coefficients = reg4.coef_ / scaler.scale_
np.testing.assert_allclose(coefficients, np.array([2, 1]), rtol=0.01)这是因为,在数学上,设置z = (x - mu)/sigma,模型reg4正在求解y = a1*z1 + a2*z2 + a0。我们可以通过简单代数:y = a1*[(x1 - mu1)/sigma1] + a2*[(x2 - mu2)/sigma2] + a0恢复y和x之间的关系,这可以简化为y = (a1/sigma1)*x1 + (a2/sigma2)*x2 + (a0 - a1*mu1/sigma1 - a2*mu2/sigma2)。
reg4.coef_ / scaler.scale_在上面的表示法中表示[a1/sigma1, a2/sigma2],这正是normalize=True为保证系数相同所做的。
模式5的得分下降。
标准化特征为零均值,但目标变量不一定是零均值。因此,不固定拦截会使模型忽略目标的均值。在我一直使用的例子中,y = 3 + ...中的"3“没有被拟合,这自然降低了模型的预测能力。:)
Stack Overflow用户
发布于 2020-08-06 17:39:13
关于fit_intercept=0和标准化数据不一致结果的最后一个问题(3)还没有得到充分的回答。
OP很可能期望StandardScaler将X和y标准化,这将使拦截必须达到0 (证明 1/3的下行方式)。
然而,StandardScaler忽略y。参见api接口。
TransformedTargetRegressor提供了一个解决方案。这种方法对于因变量的非线性转换也很有用,例如y的日志转换(但考虑这)。
下面是一个解决OP问题#3的例子:
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import make_pipeline
from sklearn.datasets import make_regression
from sklearn.compose import TransformedTargetRegressor
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import StandardScaler
import numpy as np
# define a custom transformer
class stdY(BaseEstimator,TransformerMixin):
def __init__(self):
pass
def fit(self,Y):
self.std_err_=np.std(Y)
self.mean_=np.mean(Y)
return self
def transform(self,Y):
return (Y-self.mean_)/self.std_err_
def inverse_transform(self,Y):
return Y*self.std_err_+self.mean_
# standardize X and no intercept pipeline
no_int_pipe=make_pipeline(StandardScaler(),LinearRegression(fit_intercept=0)) # only standardizing X, so not expecting a great fit by itself.
# standardize y pipeline
std_lin_reg=TransformedTargetRegressor(regressor=no_int_pipe, transformer=stdY()) # transforms y, estimates the model, then reverses the transformation for evaluating loss.
#after returning to re-read my answer, there's an even easier solution, use StandardScaler as the transfromer:
std_lin_reg_easy=TransformedTargetRegressor(regressor=no_int_pipe, transformer=StandardScaler())
# generate some simple data
X, y, w = make_regression(n_samples=100,
n_features=3, # x variables generated and returned
n_informative=3, # x variables included in the actual model of y
effective_rank=3, # make less than n_informative for multicollinearity
coef=True,
noise=0.1,
random_state=0,
bias=10)
std_lin_reg.fit(X,y)
print('custom transformer on y and no intercept r2_score: ',std_lin_reg.score(X,y))
std_lin_reg_easy.fit(X,y)
print('standard scaler on y and no intercept r2_score: ',std_lin_reg_easy.score(X,y))
no_int_pipe.fit(X,y)
print('\nonly standard scalar and no intercept r2_score: ',no_int_pipe.score(X,y))回传
custom transformer on y and no intercept r2_score: 0.9999343800041816
standard scaler on y and no intercept r2_score: 0.9999343800041816
only standard scalar and no intercept r2_score: 0.3319175799267782https://stackoverflow.com/questions/54067474
复制相似问题

