PyMC3中的噪声或门
PyMC3中的噪声或门
提问于 2019-01-29 12:52:27
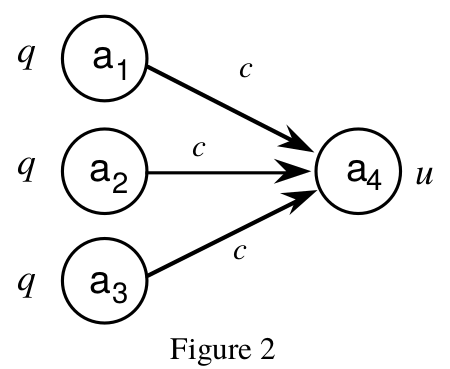
我正在尝试创建一个噪声或门的PyMC3模型(一个常见的Bayes网,见下图),其特点是Rehder (1999):
- 每一个a1、a2和a3都同样有可能独立地导致a4 : p(a4 \ ai = 1) =c for i != 4。
- 如果父节点为off,则a4启动的概率为u。
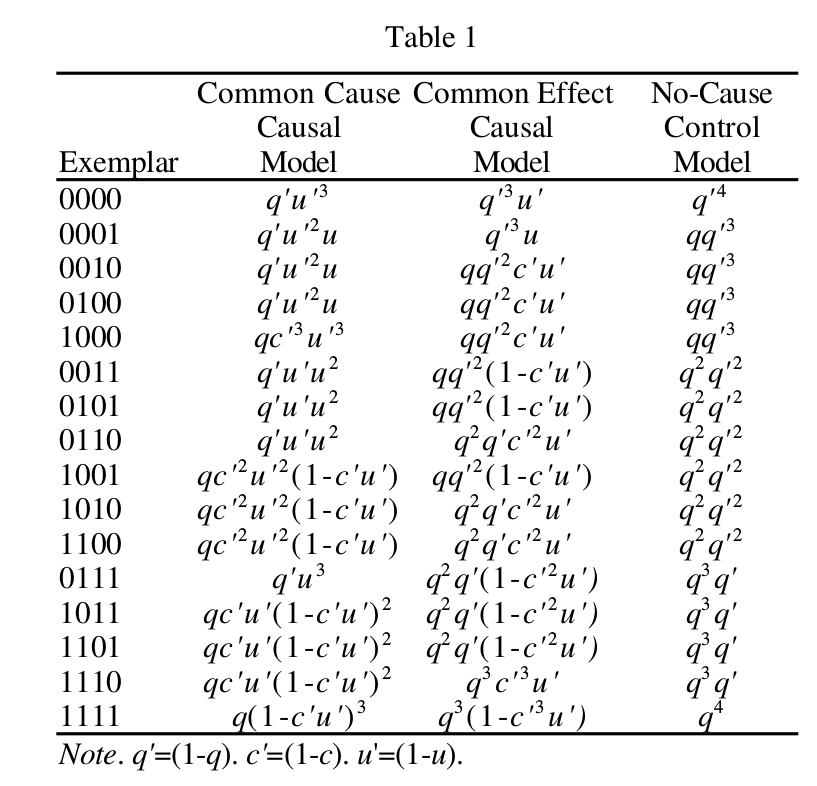
由此产生的概率分布应如下表“共同效应因果模型”下所示。Q是父母的无条件概率。
当然,我可以很容易地硬编码a4对其他三个随机变量的依赖,但是我不知道PyMC3是否有一种更紧凑的方式来表达这种分离性的交互。
参考资料: Rehder,B. (1999)。一种因果分类模型理论。“认知科学学会第21届年会议事录”*(第595-600页)。
回答 1
Stack Overflow用户
回答已采纳
发布于 2019-01-30 22:55:14
假设c是一个共享值,我认为捕获这种关系的最简洁的方法是将a_4的概率降到一个单一的概率。也就是说,类似这样的东西:
import pymc3 as pm
import theano.tensor as tt
with pm.Model() as model:
# prior probabilities
q = pm.Beta('q', alpha=1, beta=1)
c = pm.Beta('c', alpha=1, beta=1)
u = pm.Beta('u', alpha=1, beta=1)
# input nodes
a_i = pm.Bernoulli('a_i', p=q, shape=3)
# prob for a_4
p = pm.math.switch(tt.any(a_i), 1.0 - (1.0 - c)**tt.sum(a_i), u)
# output node
a_4 = pm.Bernoulli('a_4', p=p)
prior = pm.sample_prior_predictive(samples=1000)其中,如果任何一个a_i成功,那么我们计算在sum(a_i)尝试中任何成功的概率(即1-(1-c)^sum(a_i)),否则只使用u。
显然,先验概率可以根据需要被固定或变得独立(例如,您可能需要独立的q值,这将通过添加shape=3来完成)。
如果这不是你想要的,那就给这个问题加上一些澄清吧。
页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/54421539
复制相关文章
相似问题

