Networkx -寻找加权网络中最常见的路径
Networkx -寻找加权网络中最常见的路径
提问于 2019-03-10 16:04:21
我有一个有向图,有481个节点和6817个边(权重是边出现的次数,否则它大约有400万条边)。图如下所示:

我希望在大多数时间从最外层的节点找到进入图中心的路径(可能是总体权重最高的路径?)。我计算了节点的特征向量中心性,并得到了前20位。这些节点是出现在中心的节点。我试过的是:
d = g.successors(top20nodes[0])
h = g.subgraph(d)这是一种只获取最终以节点结束的节点的方法,在这种情况下,具有最高的特征向量中心性。但是,我不知道如何获得指向该节点的n条最显着(最加权)路径。
理想情况下,我的最终结果是,灰色节点只表明我只对n个最出现的路径感兴趣。在这种情况下,这4条通往中心的红色路径:
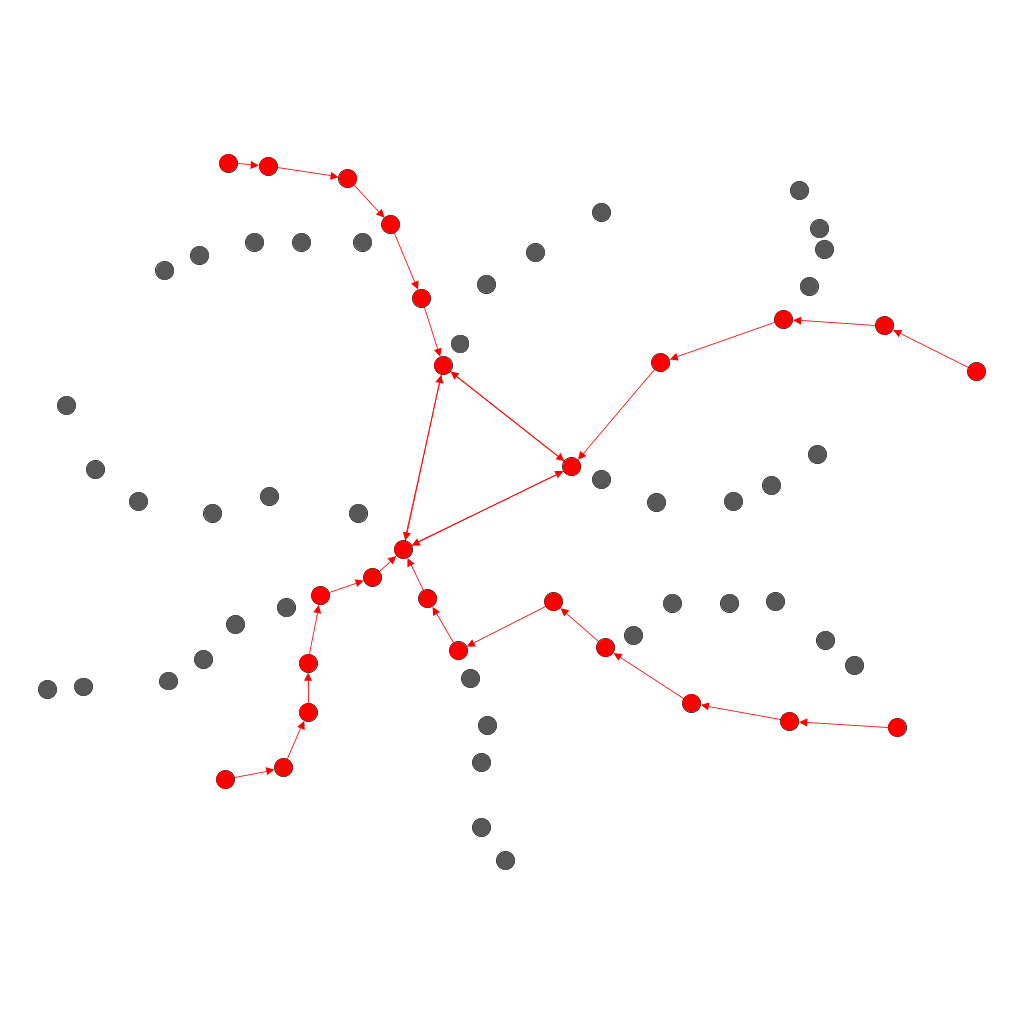
我不一定要寻找确切的代码,我只是不知道如何从这里开始。有人知道如何做到这一点吗?
回答 1
Stack Overflow用户
回答已采纳
发布于 2019-03-28 21:56:26
注意,我的解决方案不是完全最优的,在某些情况下它可以返回非最佳路径。
我给你想了个算法。它有几个假设,所以它不是最好的-最好的。但应该会有很好的结果。
首先,你应该定义你的图形中心(我把它放在算法之外)。一旦定义了它,就应该将所有中心节点替换为唯一的中心节点--主中心节点(不要忘记边缘)。之后,我的算法开始了。
它以定义的深度从中心节点启动BFS树。这是主要的不完美部分:如果在两个节点之间有两条路径--长重和短光,那么将选择短光。我不确定它是否会对你的图形至关重要,但看起来不会(图片不是很能提供信息)。
BFS树建立后,总结了BFS路径的所有分支,并对它们进行了排序。然后你可以选择第一个X路径。
我希望它能帮助你解决问题:)
import networkx as nx
# Create graph
G = nx.DiGraph()
G.add_nodes_from([1,6,7,8,9,10,11,12,13,14,15,16,17])
G.add_weighted_edges_from([
(6,1,2),
(7,1,5),
(10,1,7),
(12,1,1),
(15,1,4),
(17,1,6),
(8,6,5),
(8,7,8),
(9,8,2),
(11,10,1),
(13,12,5),
(14,13,6),
(16,15,3),
(16,14,4),
(14,16,1),
])
# Get the BFS tree. 1 is the center, 100 is the BFS length. Note, that
# long lengths MAY waste a lot of computing time
B = nx.bfs_tree(G, 1, 100)
# Get our center
root = list(v for v, d in B.in_degree() if d == 0)[0]
# Get all leaves _in_BFS_tree
leaves = (v for v, d in B.out_degree() if d == 0)
# Get all paths
all_paths = [nx.shortest_path(B, root, l) for l in leaves]
# Get all sorted pairs [path, path_length]
result = sorted(
[
(
path, sum((G.edges[path[i+1], path[i]]['weight'])
for i in range(len(path) - 1))
)
for path in all_paths
],
key=lambda x: x[1],
reverse=True
)
result
[([1, 12, 13, 14], 12),
([1, 6, 8, 9], 9),
([1, 10, 11], 8),
([1, 15, 16], 7),
([1, 17], 6),
([1, 7], 5)]页面原文内容由Stack Overflow提供。腾讯云小微IT领域专用引擎提供翻译支持
原文链接:
https://stackoverflow.com/questions/55089606
复制相关文章
相似问题

