问基于acf和pacf图确定p，q值，并根据图识别SARIMA的参数

EN

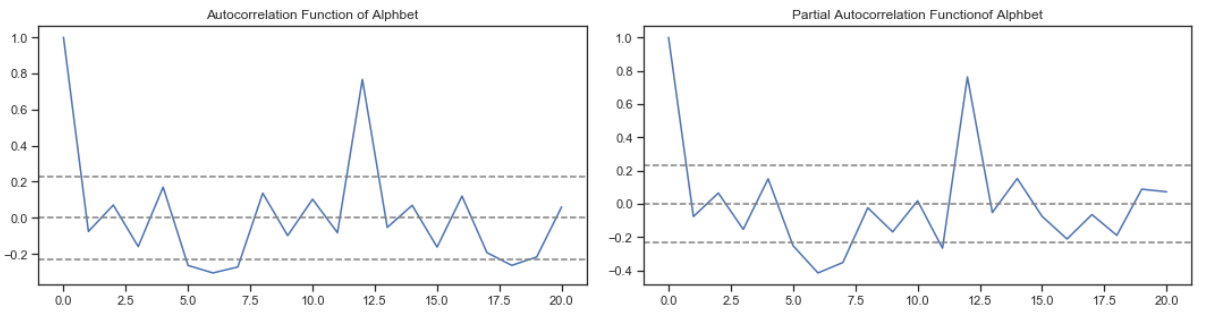
(自相关因子)

这是当前时间点的观测与前一个时间点的观测之间的相关性。

(偏自相关因子)

在我们考虑两个观测点的情况下，两个观测点之间的相关性与其他时间点的观测值是相关的。例如，今天的股价可以与前天相关联，昨天也可以与前天相关联。那么，昨天的PACF是扣除前天的影响后，今天和昨天之间的真正的相关关系。

法测定ACF和PACF

·去趋势数据

我们需要执行的首要步骤是确定数据中是否可以看到趋势的存在，如果是的话，我们需要降低数据的趋势，以便顺利地进行计算。本文第二部分讨论了从数据中消除趋势的各种方法。通常，这里使用一次滞后差分法。

·识别重要术语

使用PACF确定AR模型中使用的重要术语。术语的数量决定了模型的顺序。例如，如果昨天股票价格的PACF是显著的，而其他所有的PACF都是不显着的。那么昨天的股价将被用来预测今天的股价。这种AR模型称为一阶AR模型。它被表示为AR (1)。

类似的程序可以用于识别MA模型的重要条件。我们将使用ACF来确定MA模型中使用的重要术语。

·选择使用的模型

首先，我们应该分别用PACF和ACF计算AR和MA的重要项。然后，下一步是确定哪一个术语更简单，可以很好地用于实现。

​

​

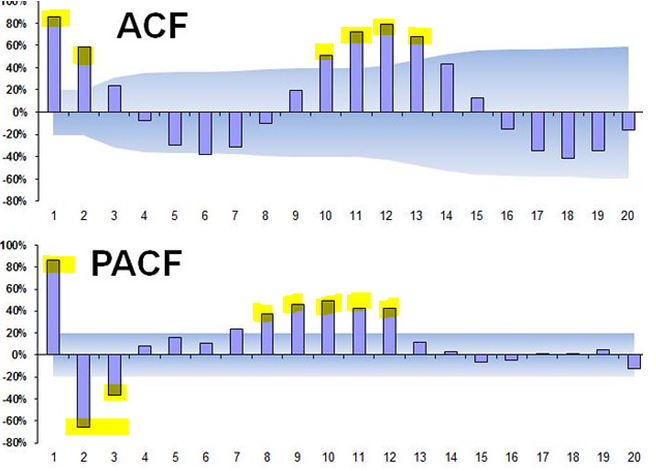
根据上面的图表，

*按ACF =6表示的重要数字

* PACF中的重要数字=8

显然，我们将在这个模型中使用MA，因为ACF < PACF。ACF =6表示如果我们使用MA模型，我们应该使用前6个时间点的观测值，这意味着MA (6)。PACF =8表示如果我们使用AR模型，我们应该使用前8个时间点的观测，这意味着AR (8)。为了降低模型的复杂度，选择了AR和MA的最小阶数。如果PACF的顺序小于ACF，我们会选择AR而不是MA。ARIMA算法代表自回归积分移动平均.这只不过是AR和MA的结合，以产生更复杂和准确的模型。在ARIMA中，“I”表示“整合”。它表示用于处理非平稳数据的差分。

对于上面显示的图表，

如果采用1级差分对数据进行退化，则积分因子为1，则可以将AR和MA相结合的模型表示为ARIMA (8，1，6)。如果采用2级差分对数据进行退化，则积分因子为2，则可以将AR和MA相结合的模型表示为ARIMA (8，2，6)。

在数学上，它被表示为ARIMA(p，d，q)

这里,

P= PACF中用于趋势的重要术语数

D=趋势差的顺序

ACF中用于趋势的重要术语的q=数

您可以参考我的文章在这里获得更多细节- URL