相似性计算方法是向量检索的基础,用于衡量高维向量数据之间的相似度。在创建 Collection 时,需要依据数据特征,选择合适的相似性计算方法。下表展示了这些广泛使用的相似性计算方法如何与各种输入数据形式和腾讯云向量数据库(Tencent Cloud VectorDB)索引相匹配。
相似性计算方法 | 数据格式 | 向量索引类型 |
内积(IP) | 浮点型 | FLAT、HNSW、IVF_RABITQ、IVF 系列 |
欧式距离(L2) | | |
余弦相似度(COSINE) | | |
汉明距离(Hamming Distance) | 二进制 | BIN_FLAT 说明: 索引类型为二进制索引时,相似性计算方法只能选择 Hamming Distance。 |
内积(IP)
全称为 Inner Product,内积也称点积,计算结果是一个数。它计算两个向量之间的点积(内积),其计算公式如下所示。其中,a = (a1, a2,..., an) 和 b = (b1, b2,..., bn) ,是 n 维空间中的两个点。计算所得值越大,越与搜索值相似。
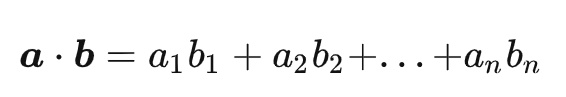
欧式距离(L2)
欧式距离(L2)全称为 Euclidean distance,指欧几里得距离。它计算两个向量点在空间中的直线距离。计算公式如下所示。其中,a = (a1, a2,..., an) 和 b = (b1, b2,..., bn) 是 n 维空间中的两个点。它是最常用的距离度量。计算所得的值越小,越与搜索值相似。L2在低维空间中表现良好,但是在高维空间中,由于维度灾难的影响,L2的效果会逐渐变差。
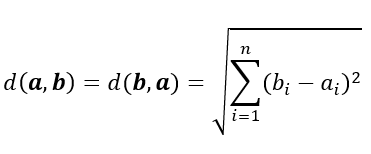
余弦相似度(COSINE)
余弦相似度(Cosine Similarity)算法,是一种常用的文本相似度计算方法。它通过计算两个向量在多维空间中的夹角余弦值来衡量它们的相似程度。其计算公式如下所示。其中,a = (a1, a2,..., an) 和 b = (b1, b2,..., bn) 是 n 维空间中的两个点。|a|与|b|分别代表 a 和 b 归一化后的值。cosθ 代表 a 与 b 之间的余弦夹角。计算所得值越大,越与搜索值相似。取值范围为[-1,1]。
说明:
在向量归一化之后,内积与余弦相似度等价。余弦相似性只考虑向量夹角大小,而内积不仅考虑向量夹角大小,也考虑了向量的长度差。
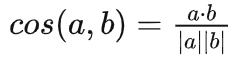
汉明距离(Hamming Distance)
汉明距离,也称为 Hamming Distance,通过计算两个字符串对应位置上不同字符的数量来定义,如果字符不同,那么它们之间的汉明距离就会加一。具体来说,对于长度为 n 的二进制向量,如果两个向量的对应位有 d 个不同,则它们的汉明距离为 d。汉明距离是一种简单而有效的相似度计算方法,尤其适用于处理等长的二进制数据。
汉明距离越小,表示两个字符串之间的相似度越高。
它是一种对称度量,即字符串 A 与字符串 B 的汉明距离与字符串 B 与字符串 A 的汉明距离相同。
例如,两个十进制数 a=93和 b=73,如果将这两个数用二进制表示的话,即 a=1011101和 b=1001001,这两者的汉明距离为2,因为它们中有两个字符不一致,即在第三和第五个位置上的字符不同。