(一)算法基础——枚举
目录
枚举
- 基于逐个尝试答案的一种问题求解策略
- 例如: 求小于N的最大素数
- – 找不到一个数学公式, 使得根据N就可以计算出这个素数
- – N-1是素数吗? N-2是素数吗? ……
- ->判断N-i是否是素数的问题
- ->转化为求小于N的全部素数(可以用筛法)
例题
1.完美立方
- 题目
形如a^3= b^3 + c^3 + d^3的等式被称为完美立方等式。例如 12^3= 6^3 + 8^3 + 10^3 。编写一个程序,对任给的正整数N (N≤100),寻找所有的四元组(a, b, c, d),使得a ^3 = b^3 + c ^3 + d^3,其中a,b,c,d 大于 1, 小于等于N,且b<=c<=d。
- 输入
一个正整数N (N≤100)。
- 输出
每行输出一个完美立方。输出格式为: Cube = a, Triple = (b,c,d) 其中a,b,c,d所在位置分别用实际求出四元组值代入。
- 要求
请按照a的值,从小到大依次输出。当两个完美立方 等式中a的值相同,则b值小的优先输出、仍相同 则c值小的优先输出、再相同则d值小的先输出。
- 样例输入
24
- 样例输出
Cube = 6, Triple = (3,4,5) Cube = 12, Triple = (6,8,10) Cube = 18, Triple = (2,12,16) Cube = 18, Triple = (9,12,15) Cube = 19, Triple = (3,10,18) Cube = 20, Triple = (7,14,17) Cube = 24, Triple = (12,16,20)
解题思路
本题目前找不到一个高效的办法,就只能先通过多层循环来解决,但是在循环的过程中,要注意循环的范围,避免一些无效的运算,以此来提高效率。 a枚举范围[2,N] b范围 [2,a-1] c范围 [b,a-1] d范围 [c,a-1]
代码实现如下所示
#include<stdio.h>
int main(void)
{
//输入部分
int N;
scanf("%d", &N);
//循环部分
int a, b, c,d;
for (a = 2; a <= N; a++){
for(b = 2; b <= a - 1; b++){
for(c = b; c <= a - 1; c++){
for(d = c; d <= a - 1; d++){
if(a*a*a == b*b*b + c*c*c + d*d*d)
printf("Cube = %d, Triple = (%d,%d,%d)\n", a, b, c, d);
}
}
}
}
return 0;
}运行效果如下所示
总结
本题难度不大,也没有什么技巧,主要的问题就是控制好循环的范围,避免一些无效计算。
2.生理周期
- 题目
人有体力、情商、智商的高峰日子,它们分别每隔 23天、28天和33天出现一次。对于每个人,我们想 知道何时三个高峰落在同一天。给定三个高峰出现 的日子p,e和i(不一定是第一次高峰出现的日子), 再给定另一个指定的日子d,你的任务是输出日子d 之后,下一次三个高峰落在同一天的日子(用距离d 的天数表示)。例如:给定日子为10,下次出现三 个高峰同一天的日子是12,则输出2。
- 输入
输入四个整数:p, e, i和d。 p, e, i分别表示体力、情感和智力 高峰出现的日子。d是给定的日子,可能小于p, e或 i。所有给 定日子是非负的并且小于或等于365,所求的日子小于或等于 21252。
- 输出
从给定日子起,下一次三个高峰同一天的日子(距离给定日子 的天数)。
- 输入样例
0 0 0 0 0 0 0 100 5 20 34 325 4 5 6 7 283 102 23 320 203 301 203 40 -1 -1 -1 -1
- 输出样例
Case 1: the next triple peak occurs in 21252 days. Case 2: the next triple peak occurs in 21152 days. Case 3: the next triple peak occurs in 19575 days. Case 4: the next triple peak occurs in 16994 days. Case 5: the next triple peak occurs in 8910 days. Case 6: the next triple peak occurs in 10789 days.
解题思路
一开始想的是直接从d+1试到21252,但后来发现这样太慢了,之后听老师讲解后,选择了更快一点的解法,即跳跃式寻找,先找到体力高峰,在每次增加23天进行判断,找到情商高峰,再一次加23*28天,找到智商高峰,这样就比之前判断的更少。
代码实现如下
#include<stdio.h>
int main(void)
{
int p, e, i, d, n = 0;
// 输入
while(scanf("%d %d %d %d",&p ,&e ,&i ,&d) && p!=-1){
//用来计数
++n;
int k;
// 找到体力高峰
for(k = d+1; (k - p) % 23; ++k);
//找到情商高峰
for(; (k - e) % 28; k += 23);
// 找到智商高峰
for(; (k - i) % 33; k += 23 * 28);
printf("Case %d : the next triple peak occurs in %d days.\n",n,k - d);
}
return 0;
}运行结果如下所示
总结
本题也是一样的,既然不能避免遍历,那就减少判断的次数,来达到优化的效果。
3.假币问题
- 题目
有12枚硬币。其中有11枚真币和1枚假币。假币和真 币重量不同,但不知道假币比真币轻还是重。现在, 用一架天平称了这些币三次,告诉你称的结果,请你 找出假币并且确定假币是轻是重(数据保证一定能找 出来)。
- 输入
第一行是测试数据组数。 每组数据有三行,每行表示一次称量的结果。银币标号为 A-L。每次称量的结果用三个以空格隔开的字符串表示: 天平左边放置的硬币 天平右边放置的硬币 平衡状态。其 中平衡状态用``up'', ``down'', 或 ``even''表示, 分别为右 端高、右端低和平衡。天平左右的硬币数总是相等的。
- 输出
输出哪一个标号的银币是假币,并说明它比真币轻还是重。
- 输入样例
1 ABCD EFGH even ABCI EFJK up ABIJ EFGH even
- 输出样例
K is the counterfeit coin and it is light.
解题思路
一开始想假设硬币是轻的,就直接去翘起来的一端去找,找不到之后再假设硬币是重的,去降下来的一端找,后来发现这样写出来的代码不但不好理解,而且还不能有效的解决问题,代码耦合性也较高。后来就对于每一枚硬币先假设它是轻的,看这样是否符合称量结果。如果符合,问题即解决。如果不符合,就假设它是重的,看是否符合称量结果。如此遍历一遍,就能找到特殊的硬币。
代码如下所示
#include <stdio.h>
#include <string.h>
char Left[3][5]; //天平左边硬币
char Right[3][5]; //天平右边硬币
char result[3][5]; //结果
bool IsFake(char c,bool light) ;
int main(void) {
int t;
scanf("%d", &t);
while(t--) {
// 输入
for(int i = 0;i < 3; i++) scanf("%s %s %s",&Left[i],&Right[i],&result[i]);
//遍历
for(char c='A'; c<='L';c++) {
// 如果是轻的假币
if( IsFake(c,true) ){
printf("%c is the counterfeit coin and it is light.\n", c);
break;
}
// 如果是重的假币
else if( IsFake(c,false) ){
printf("%c is the counterfeit coin and it is heavy.\n", c);
break;
}
}
}
return 0;
}
bool IsFake(char c,bool light)
//light 为真表示假设假币为轻,否则表示假设假币为重
{
for(int i = 0;i < 3; i++) {
char * pLeft,*pRight; //指向天平两边的字符串
if(light) {
pLeft = Left[i];
pRight = Right[i];
}else {
//如果假设假币是重的,则把称量结果左右对换,这样能使代码统一化,相对于转换成轻的假币
pLeft = Right[i];
pRight = Left[i];
}
switch(result[i][0]) { //天平右边的情况
case 'u':
//如果右边翘起来时,右边没有这个字符,就说明不是轻的假币
if ( strchr(pRight,c) == NULL)
return false;
break;
case 'e':
//如果平衡时有这个字符,就说明不是假币
if( strchr(pLeft,c) || strchr(pRight,c))
return false;
break;
case 'd':
//如果左边翘起来时,左边没有这个字符,就说明不是轻的假币
if ( strchr(pLeft,c) == NULL)
return false;
break;
}
}
return true;
}运行结果如下所示
总结
本题难度也不大,但是一开始思路错了,导致代码比较复杂,还不好理解,在尝试优化代码后也没有特别好的办法,就还是选择了这种易于理解的解法。
4.熄灯问题
- 题目
有一个由按钮组成的矩阵, 其中每行有6个按钮, 共5行
- 每个按钮的位置上有一盏灯
- 当按下一个按钮后, 该按钮以及周围位置(上边, 下边, 左 边, 右边)的灯都会改变状态
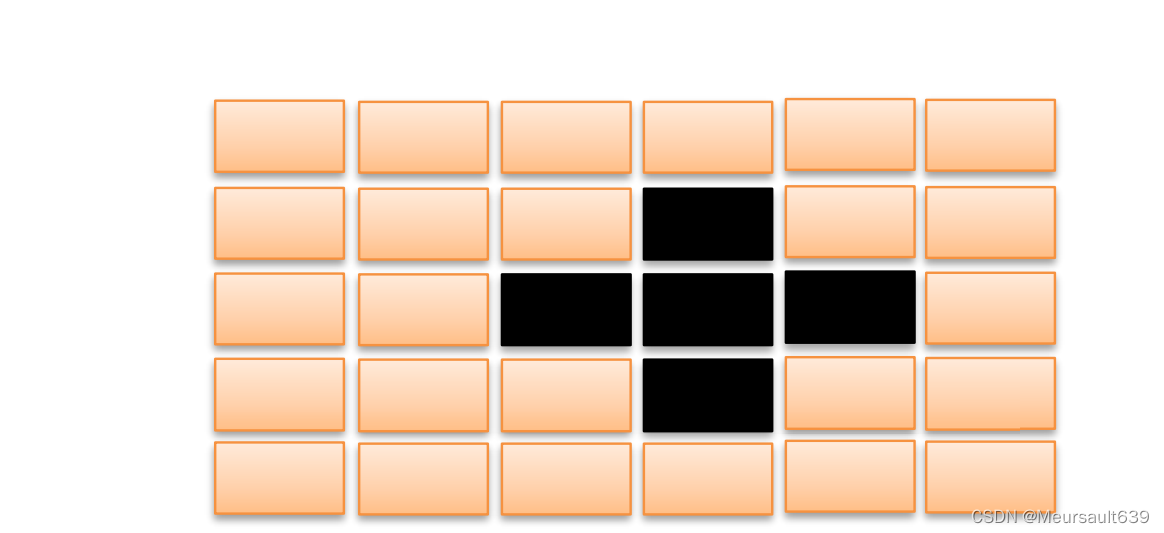
- 如果灯原来是点亮的, 就会被熄灭
- 如果灯原来是熄灭的, 则会被点亮
- 在矩阵角上的按钮改变3盏灯的状态
- 在矩阵边上的按钮改变4盏灯的状态
- 其他的按钮改变5盏灯的状态
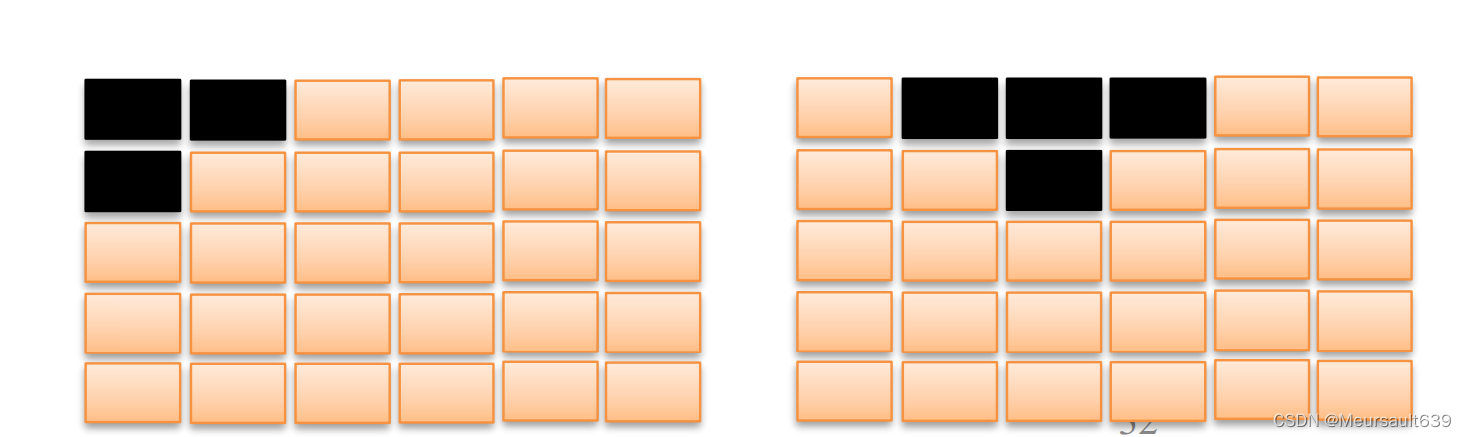
与一盏灯毗邻的多个按钮被按下时,一个操作会抵消另一次操作的结果 给定矩阵中每盏灯的初始状态,求一种按按钮方案,使得所有的灯都熄灭
- 输入
- 第一行是一个正整数N, 表示需要解决的案例数
- 每个案例由5行组成, 每一行包括6个数字
- 这些数字以空格隔开, 可以是0或1
- 0 表示灯的初始状态是熄灭的
- 1 表示灯的初始状态是点亮的
- 输出
对每个案例, 首先输出一行, 输出字符串 “PUZZLE #m”, 其中m是该案例的序号 接着按照该案例的输入格式输出5行 1 表示需要把对应的按钮按下 0 表示不需要按对应的按钮 每个数字以一个空格隔开

解题思路
暴力解法肯定是不行的,就只能用局部推整体,有点像分治的思想,就是先确定第一行的按下方式,之后第二行的按下数据也定好了,当这样操作5次之后,如果第五行为0,也就是全熄灭,就说明这样的第一行数据可以熄灭全部的灯。
代码如下所示
#include<stdio.h>
#include<string.h>
void SetBit(char &c, int i,int v);
int GetBit(char c, int i);
void FlipBit(char &c, int i);
void OutputResult(int t,char result[]);
int main(void)
{
char oriLights[5]; //最初灯矩阵,一个比特表示一盏灯
char Lights[5]; //不停变化的灯矩阵
char result[5]; //结果开关矩阵
int T, t, i, j,n;
scanf("%d", &T);
for(t = 1; t <= T; ++t) {
for(i = 0; i < 5; ++i)
// 输入
for(j = 0; j < 6; ++j){
int s;
scanf("%d", &s);
SetBit(oriLights[i], j,s);
}
//遍历首行开关的64种状态
for(n = 0; n < 64; ++n){
int switchs = n;
memcpy(Lights, oriLights, sizeof(oriLights));
for(i = 0; i < 5; ++i){
result[i] = switchs;
// 第J列
for(j = 0; j < 6; j++){
if(GetBit(switchs,j)){
// 设定第j行
if(j > 0){
// 左边
FlipBit(Lights[i],j-1);
}
FlipBit(Lights[i],j);
if(j < 4)
//右灯
FlipBit(Lights[i], j+1);
}
}
//设定下一行
if(i < 4){
Lights[i + 1] ^= switchs;
}
//把这一行的数据传回去
switchs = Lights[i];
}
if(Lights[4] == 0){
OutputResult(t,result);
break;
}
}
}
return 0;
}
// 获取到数据
int GetBit(char c, int i)
{
return (c >> i) & 1;
}
// 设定数据
void SetBit(char &c, int i,int v)
{
if(v){
c |= (1 << i);
}else{
c &= ~(1 << i);
}
}
// 翻转数据
void FlipBit(char &c, int i)
{
c ^= (1 << i);
}
void OutputResult(int t,char result[])
{
int i, j;
printf("PUZZLE # %d\n",t);
for(i = 0; i < 5; ++i){
for(j = 0; j < 6; ++j){
printf("%d",GetBit(result[i], j));
if(j < 5){
printf(" ");
}
}
printf("\n");
}
} 运行结果如下所示
总结
首先是用局部推整体的思想,先确定第一行,后面的自然就确定下来了。第二个 就是使用char类型去储存变量,然后运用位运算去操作,不过这样的操作在单片机中比较常见,也能对单片机的编程提供一种思路。
关于枚举的例子就只有这么点了,我们继续后面的学习。

