(三)算法基础——递归(2)
目录
这篇文章是上篇文章的延续,所以不会对递归进行详细的介绍,如果对递归还不太清楚的同学可以去康康上篇文章哦!
例题
1.四则运算表达式求值
- 题目
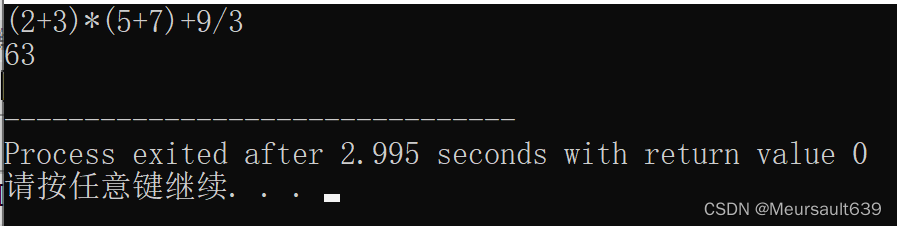
输入为四则运算表达式,仅由整数、+、-、 * 、/ 、(、) 组成,没有空格,要求求其值。假设运算符结果都是整数 。"/"结果也是整数
- 样例输入
(2+3)*(5+7)+9/3
- 样例输出
63
解题思路
首先我们需要理解表达式的定义,其实表达式也是通过递归来定义的,我们来看一看吧!
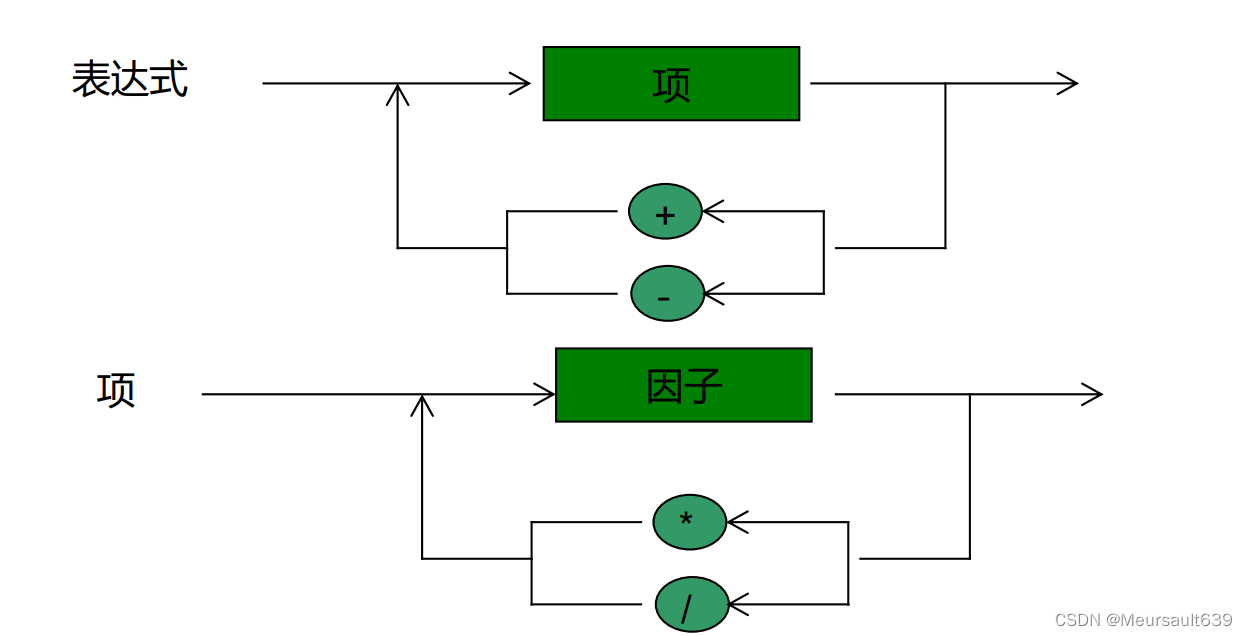
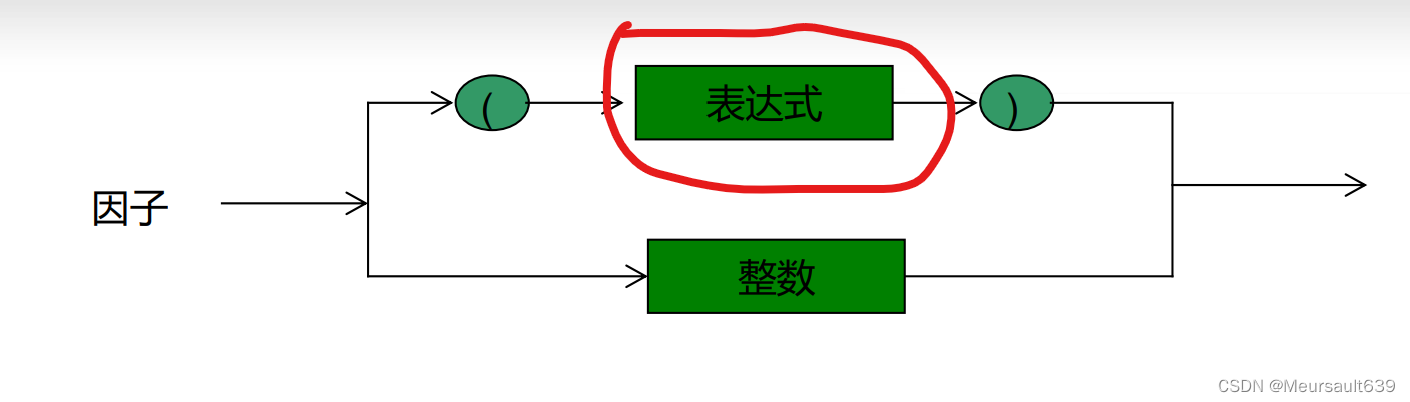
首先,表达式由项通过加减得到,项通过因子的乘除得到,而因子由整数或者表达式组成,至此,表达式再次出现了,所以他其实是满足递归的,所以我们首先考虑使用递归来解决。之所以要变成递归的形式来解决,就是因为优先级这个概念对于计算机来说是比较难处理的。所以接下来就只要处理好这三部分,就可以解决问题了。
代码实现如下所示:
// 用纯C有点困难,就先用C++解了,这个是直接操作输入流来实现的
#include <iostream>
#include <cstring>
#include <cstdlib>
using namespace std;
int factor_value();
int term_value();
int expression_value();
int main(){
cout << expression_value() << endl;
return 0;
}
int expression_value() //求一个表达式的值
{
int result = term_value(); //求第一项的值
bool more = true;
while( more) {
char op = cin.peek(); //看一个字符,不取走
if( op == '+' || op == '-' ) {
cin.get(); //从输入中取走一个字符
int value = term_value();
if( op == '+' ) result += value;
else result -= value;
}
else more = false;
}
return result;
}
int term_value() //求一个项的值
{
int result = factor_value(); //求第一个因子的值
while(true) {
char op = cin.peek();
if( op == '*' || op == '/') {
cin.get();
int value = factor_value();
if( op == '*')
result *= value;
else result /= value;
}
else
break;
}
return result;
}
int factor_value() //求一个因子的值
{
int result = 0;
char c = cin.peek();
if( c == '(') {
cin.get();
result = expression_value();
cin.get();
}
else {
while(isdigit(c)) {
result = 10 * result + c - '0';// 减去0的AscII码,得到的就是数字的大小
// 得到整数的值
cin.get();
c = cin.peek();
}
}
return result;
}运行结果如下所示:
总结
这道题目属于递归形式定义的问题 ,首先加强了分析问题的能力;其次,学到了许多的C++中操作输入流的知识,这个是我之前从未接触过的,今天算是第一次吧!
2.爬楼梯
- 题目
树老师爬楼梯,他可以每次走1级或者2级,输入楼梯的级数, 求不同的走法数。 例如:楼梯一共有3级,他可以每次都走一级,或者第一次走一 级,第二次走两级,也可以第一次走两级,第二次走一级,一 共3种方法。
- 输入
输入包含若干行,每行包含一个正整数N,代表楼梯级数,1 <= N <= 30输出不同的走法数,每一行输入对应一行 爬楼梯
- 输出
不同的走法数,每一行输入对应一行输出
- 样例输入
5 8 10
- 样例输出
8 34 89
解题思路
这个就属于用递归将问题分解为规模更小的子问题进行求解,有点像求阶乘和汉诺塔问题一样,就是找到基准情况,然后不断推进。
- 基准情况
当没有台阶或者只有一个台阶的时候,只有一种走法。
- 不断推进
f(n) = f(n-1)+f(n-2)
代码实现如下所示
#include <stdio.h>
int stairs(int n)
{
if( n == 0 || n == 1)
return 1;
return stairs(n-1) + stairs(n-2);
}
int main()
{
int N;
while(scanf("%d",&N)) {
printf("%d", stairs(N));
}
return 0;
}运行结果如下所示:

总结
这道题目本身不难,相对来说,不断推进的条件比较好找,基准条件相对多一点,但也比较好找,主要的收获就是利用递归来解决问题,只要注意基准条件和不断推进就行。
3.放苹果
- 题目
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放, 问共有多少种不同的分法?5,1,1和1,5,1 是同一种分法。
- 输入
第一行是测试数据的数目t(0 <= t <= 20)。以下每行均包含二个整 数M和N,以空格分开。1<=M,N<=10。
- 输出
对输入的每组数据M和N,用一行输出相应的K。
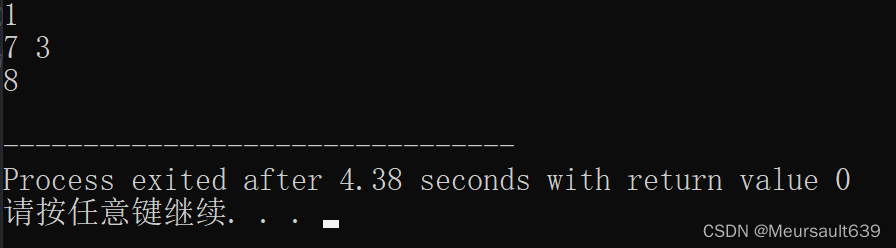
- 样例输入
1 7 3
- 样例输出
8
解题思路
一开始没有什么思路,因为这里面涉及盘子以及苹果的个数,所以基准情况应该是盘子为0或苹果为0,但是不断推进的条件有点多,所以需要分析一下才能得到结果。
- 基准情况
盘子为0或苹果为0
- 不断推进
设i个苹果放在k个盘子里放法总数是 f(i,k) k > i 时, f(i,k) = f(i,i) k <= i 时,总放法 = 有盘子为空的放法+没盘子为空的放法 f(i,k) = f(i,k-1) + f(i-k,k)
代码如下所示
#include <stdio.h>
int f(int m,int n) {
if( n > m )// 盘子数大于苹果数时,相当于把m个苹果放到m个盘子里面去。
return f(m,m);
if( m == 0)// 苹果数为0
return 1;
if( n == 0 )// 盘子数为0
return 0;
return f(m,n-1) + f(m-n,n);
/*有盘子为空,说明最少一个盘子为空 ,相当于 f(m,n-1)
没有盘子为空时,相当于每个盘子放一个苹果,之后就是 f(m-n,n)*/
}
int main() {
int t,m,n;
scanf("%d",&t);
while( t--) {
scanf("%d %d", &m,&n);
printf("%d\n",f(m,n));
}
return 0;
}运行结果如下所示
总结
这道题目主要就是不断推进的条件比较多,需要去判断和分析 ,而基准条件相对好判断一点。
4.算24
- 题目
给出4个小于10个正整数,你可以使用加减乘除4种运算以及括 号把这4个数连接起来得到一个表达式。现在的问题是,是否存 在一种方式使得得到的表达式的结果等于24。 这里加减乘除以及括号的运算结果和运算的优先级跟我们平常 的定义一致(这里的除法定义是实数除法)。 比如,对于5,5,5,1,我们知道5 * (5 – 1 / 5) = 24,因此 可以得到24。又比如,对于1,1,4,2,我们怎么都不能得到 24。
- 输入
输入数据包括多行,每行给出一组测试数据,包括4个小于10个正整 数。最后一组测试数据中包括4个0,表示输入的结束,这组数据不用 处理。
- 输出
对于每一组测试数据,输出一行,如果可以得到24,输出“YES”; 否则,输出“NO”。
- 样例输入
5 5 5 1 1 1 4 2 0 0 0 0
- 样例输出
YES NO
解题思路
这道题目的基准情况以及不断推进条件都比较好找,但难就难在不断推进的条件特别多,要一一尝试所有方法。
- 基准条件
判断一个数是不是24
- 不断推进
n个数算24,必有两个数要先算。这两个数算的结果,和剩余n-2个数,就构成了n-1个数求24的问题
代码如下所示:
#include <stdio.h>
#include <math.h>
#include<stdbool.h>
// 用来判断精度
#define EPS 1e-6
//判断是否为0,因为浮点数不能直接用==比较大小
bool isZero(double x) {
return fabs(x) <= EPS;
}
//用数组a里的 n个数,计算24
bool count24(double a[],int n)
{
int i,j,k;
//基准条件
if( n == 1 ) {
if(isZero( a[0] - 24) )
return true;
else
return false;
}
//临时存放数字
double b[5];
//枚举两个数的组合
for(i = 0;i < n-1; ++i)
for(j = i+1;j < n; ++j) {
int m = 0; //还剩下m个数, m = n - 2
for(k = 0; k < n; ++k)
if( k != i && k!= j)
b[m++] = a[k];//把其余数放入b
//开始计算
b[m] = a[i]+a[j];
if(count24(b,m+1))
return true;
b[m] = a[i]-a[j];
if(count24(b,m+1))
return true;
b[m] = a[j]-a[i];
if(count24(b,m+1))
return true;
b[m] = a[i]*a[j];
if(count24(b,m+1))
return true;
//分母不能为0
if( !isZero(a[j])) {
b[m] = a[i]/a[j];
if(count24(b,m+1))
return true;
}
if( !isZero(a[i])) {
b[m] = a[j]/a[i];
if(count24(b,m+1))
return true;
}
}
return false;
}
int main()
{
int i,ab;
double a[5],r;
int c[5];
while(true) {
for(i = 0;i<4;i++)
scanf("%lf", &a[i] );
if( isZero(a[0]))
break;
if( count24(a,4))
printf("YES\n");
else
printf("NO\n");
}
return 0;
}运行结果如下所示

总结
本题还是普通递归的思想,只不过不断推进的条件稍微复杂一点,稍加注意就好了!
好了,我们先到这,之后还会不断更新!

