黄金分割法(一维搜索算法)
一维搜索算法之黄金分割法
1、概述
黄金分割法是一种区间收缩方法。
所谓区间收缩方法,指的是将含有最优解的区间逐步缩小,直至区间长度为零的方法。比如,为求函数f(x)在区间[a,b]上的最小值点,可在该区间中任取两点
,通过比较函数f(x)在这两点的函数值或者导数值等,来决定去掉一部分区间[a,
]或者[
,b],从而使搜索区间长度变小,如此迭代,直至区间收缩为一点为止,或区间长度小于某给定的精度为止。
对于区间[a,b]上的单峰函数f(x),可以在其中任意选取两点
,通过比较这两点的函数值,就可以将搜索区间缩小。比如说,如果f(
)<f(
),则选取[
]=[a,
],如果f(
)> f(
),则选取[
]=[
,b],如果f(
)=f(
),则选取[
]=[
],这样就得到f(x)的更小的搜索区间[
],然后根据这一方法再进行划分,得到一系列搜索区间满足
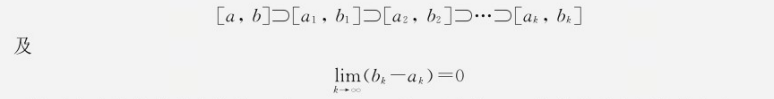
于是对事先给定的某个精度
,当
时,可以将f(x)的最小值点近似地取为
单峰函数与搜索区间的定义如下:


如何选取x1和x2才能使得算法的效率更高? 这里推导过程不在详细讨论,直接给出满足对称取点、等比收缩和单点计算三个原则的分点。
或者
2、黄金分割法
算法描述如下:

这个算法非常理想,整个迭代过程中。除最初计算分点时使用过一次乘法外,后边的分点全部都由加减法完成,并且每次迭代只需计算一个分点的函数值。但是,在实际应用中,该方法存在一定的缺陷。这种缺陷主要来源于无理数
的取值。这里我们只取了小数点后三位数。因而有一定误差,所以在迭代过程中,经过多次累计,误差就会很大,从而导致最终选取的两点并不一定是我们所期望的那两点,事实上,常常发生x2小于x1的情形。 为避免这种情况的出现,我们也可以通过将无理数
小数点后面的位数提高来避免算法的这一缺陷。不过这样做的效果未必很好。因为我们不知道在算法中到底要经过多少次迭代,当迭代次数很大时,这种做法依然是不能奏效的。因此,我们在程序中每次计算分点时不得不根据算法原理,使用一次乘法,即第二个分点不用加减法产生,而直接用乘法计算得出。由此即可避免累计误差所带来的缺陷。我们仍假设f(x)是区间[a,b]上的单峰函数。修改后的黄金分割法的计算框图如下图所示。
3、修改后的黄金分割算法
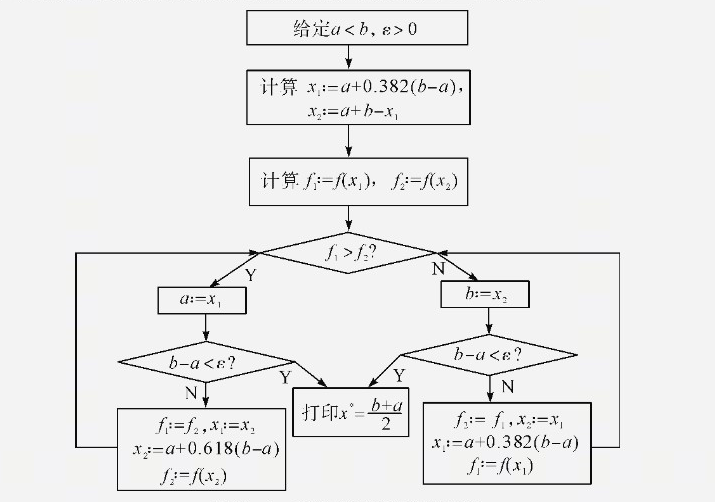
修改后的黄金分割算法如下:
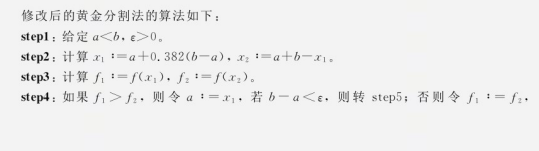

4、编程实现修改后的黄金分割算法
用黄金分割法求函数
在区间
上的最小值点,取
。
import java.math.BigDecimal;
/**
* 黄金分割法测试
*/
public class GoldenCut {
public static final BigDecimal C=new BigDecimal("0.01");
public static BigDecimal end=null;
/**
*x^3-12x-11
* @param x 输入参数x
* @return x^3-12x-11
*/
public static BigDecimal ComputeFx(BigDecimal x){
return x.pow(3).subtract(new BigDecimal("12").multiply(x)).subtract(new BigDecimal("11"))
.setScale(10,BigDecimal.ROUND_HALF_EVEN);
}
/**
* a+0.382*(b-a)
* @param a
* @param b
* @return a+0.382*(b-a)
*/
public static BigDecimal Compute382(BigDecimal a,BigDecimal b){
return a.add(new BigDecimal("0.382").multiply(b.subtract(a)))
.setScale(10,BigDecimal.ROUND_HALF_EVEN);
}
/**
* a+0.618(b-a)
* @param a
* @param b
* @return
*/
public static BigDecimal Compute618(BigDecimal a,BigDecimal b){
return a.add(new BigDecimal("0.618").multiply(b.subtract(a)))
.setScale(10,BigDecimal.ROUND_HALF_EVEN);
}
/**
* a+b-x1
* @param a
* @param b
* @param x1
* @return
*/
public static BigDecimal Subtractabx1(BigDecimal a,BigDecimal b,BigDecimal x1){
return a.add(b).subtract(x1)
.setScale(10,BigDecimal.ROUND_HALF_EVEN);
}
//判断是否满足精度 b-a<C?
public static boolean OK(BigDecimal a,BigDecimal b){
return b.subtract(a).compareTo(C) < 0;
}
//输出最优解
public static BigDecimal Success(BigDecimal a, BigDecimal b){
return (a.add(b)).divide(new BigDecimal("2"))
.setScale(10,BigDecimal.ROUND_HALF_EVEN);
}
//修改后的黄金分割法
public static void goldenTest1(BigDecimal a,BigDecimal b){
System.out.println("初始化");
BigDecimal x1=Compute382(a,b);
BigDecimal x2=Subtractabx1(a,b,x1);
BigDecimal f1=ComputeFx(x1);
BigDecimal f2=ComputeFx(x2);
System.out.println("x1="+x1);
System.out.println("x2="+x2);
System.out.println("f1="+f1);
System.out.println("f2="+f2);
System.out.println("迭代区间如下:");
int count=0; //迭代次数
while(!OK(a,b)){//只要不满足精度就一直迭代
System.out.println("["+a+"\t,\t"+b+"]");
count++; //迭代次数+1
if(f1.compareTo(f2)==1){//f1>f2
a=x1;
if(OK(a,b)){ //精度判断
end = Success(a, b);
break;
}else{
f1=f2;
x1=x2;
x2=Compute618(a,b);
f2=ComputeFx(x2);
}
}else{
b=x2;
if(OK(a,b)){
end = Success(a, b);
break;
}else{
f2=f1;
x2=x1;
x1=Compute382(a,b);
f1=ComputeFx(x1);
}
}
}
System.out.println("迭代结束,迭代次数"+count);
}
public static void main(String[] args) {
BigDecimal a=new BigDecimal("0");
BigDecimal b=new BigDecimal("10");
goldenTest1(a,b);
System.out.println("最优解为x*="+end);
System.out.println("f(x*)="+ComputeFx(end));
}
}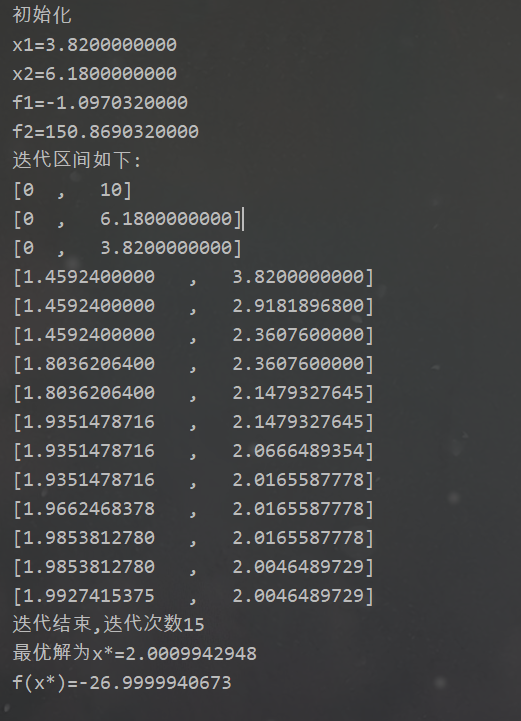
由运行结果可以看到,迭代次数15次,最优解为
。迭代区间如下:
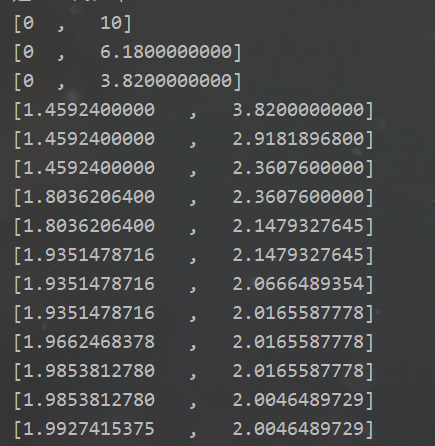
可以证明,黄金分割法是线性收敛的。

