【运筹学】线性规划数学模型 ( 单纯形法 | 最优解判定原则 | 线性规划求解示例 )

韩曙亮

发布于 2023-03-28 16:22:31

1.9K0

文章被收录于专栏：韩曙亮的移动开发专栏韩曙亮的移动开发专栏

文章目录

在上一篇博客【运筹学】线性规划数学模型 ( 单纯形法 | 最优解判定原则 | 单纯形表 | 系数计算方法 | 根据系数是否小于等于 0 判定最优解 ) 博客中讲解了最优解判定原则 , 基本原理就是

目标函数推导后的结果

maxZ = b_0 + ( C_N^T - C_B^T B^{-1}N )X_N

;

如果满足条件 : " 当

X_N = O

时 , 目标函数取值最大 " , 那么该

B

矩阵对应的基可行解就是最优解 ( 根据定理得出 ) ;

在

( C_N^T - C_B^T B^{-1}N )

计算结果中 , 每个分量的值都小于等于

0

时 , 该解就是最优解 ;

将

C_N

,

C_B

,

B^{-1}N

写入单纯形表中 , 方便计算 ;

( C_N^T - C_B^T B^{-1}N ) = \begin{pmatrix} c_{m+1} \quad c_{m+2} \quad \cdots \quad c_n \end{pmatrix} - \begin{pmatrix} c_{1} \quad c_{2} \quad \cdots \quad c_m \end{pmatrix} \times \begin{bmatrix} &a_{1,m+1} & \cdots & a_{1n} & \\\\ &\vdots & \vdots & \vdots & \\\\ &a_{m,m+1} & \cdots & a_{mn} & \end{bmatrix}

根据上述公式 , 每个系数的计算公式为 :

\sigma_j = c_j - \sum c_i a_{ij}

, 其中

c_j

对应的是非基变量在目标函数系数 ,

c_i

是基变量在目标函数中的系数 ,

a_{ij}

是

B^{-1}N

中的矩阵向量 , 代表一列 ;

单纯形法解线性规划的三大问题 : 查找初始基可行解 , 判定是否是最优解 , 如何迭代基可行解 ;

在前几篇博客中讲解了如何查找初始基可行解 , 与判定是否是最优解 , 本篇博客中讲解如何进行迭代 ;

一、单纯形法计算示例

使用单纯形法求解线性规划最优解 :

\begin{array}{lcl} max Z = 3x_1 + 4x_2 \\ \\ \begin{cases} 2 x_1 + x_2 \leq 40 \\\\ x_1 + 3x_2 \leq 30 \\ \\x_j \geq 0 & (j = 1 , 2 ) \end{cases}\end{array}

二、转化标准形式

首先将该线性规划转为标准形式 :

① 变量约束 : 首先查看变量约束 , 两个变量都是

\geq 0

的 , 符合线性规划标准形式要求 ;

② 不等式转换 : 两个等式都是小于等于不等式 , 需要在不等式左侧加入松弛变量 , 将其转为等式 ;

2 x_1 + x_2 \leq 40

, 左侧加入松弛变量

x_3

, 变为

2 x_1 + x_2 + x_3 = 40

x_1 + 3x_2 \leq 30

, 左侧加入松弛变量

x_4

, 变为

x_1 + 3x_2 + x_4 = 30

③ 更新目标函数 : 将

x_3

和

x_4

加入到目标函数中 , 得到新的目标函数

max Z = 3x_1 + 4x_2 + 0x_3 + 0x_4

;

此时线性规划标准形式为 :

\begin{array}{lcl} max Z = 3x_1 + 4x_2 + 0x_3 + 0x_4 \\ \\ \begin{cases} 2 x_1 + x_2 + x_3 + 0x_4 = 40 \\\\ x_1 + 3x_2 + 0x_3 + x_4 = 30 \\\\ x_j \geq 0 & (j = 1 , 2 , 3 , 4 ) \end{cases}\end{array}

三、查找初始基可行解

找基矩阵 :

上述线性规划标准形式的系数矩阵为

\begin{bmatrix} &2 & 1 & 1 & 0 & \\\\ & 1 & 3 & 0 & 1 & \end{bmatrix}

, 其中子矩阵中有

\begin{bmatrix} & 1 & 0 & \\\\ & 0 & 1 & \end{bmatrix}

单位阵

I

;

使用该单位阵

I

作为基矩阵 , 单位阵肯定是可逆的 , 其对应的基解 , 解出后的值就是右侧的常数值 , 肯定大于等于

0

, 是基可行解 ;

四、列出单纯形表

列出单纯形表 :

c j c_j cj	c j c_j cj		3 3 3	4 4 4	0 0 0	0 0 0
C B C_B CB 基变量系数 (目标函数)	基变量	常数 b b b	x 1 x_1 x1	x 2 x_2 x2	x 3 x_3 x3	x 4 x_4 x4	θ i \theta_i θi
0 0 0 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3 )	x 3 x_3 x3	40 40 40	2 2 2	1 1 1	1 1 1	0 0 0
0 0 0 ( 目标函数 x 4 x_4 x4 系数 c 4 c_4 c4)	x 4 x_4 x4	30 30 30	1 1 1	3 3 3	0 0 0	1 1 1
		σ j \sigma_j σj	3 3 3	4 4 4	0 0 0	0 0 0

c_j

3

4

0

C_B

基变量系数 (目标函数)基变量常数

b

x_1

x_2

x_3

x_4

\theta_i

0

( 目标函数

x_3

系数

c_3

)

x_3

40

2

1

0

( 目标函数

x_4

系数

c_4

)

x_4

30

1

3

0

1

\sigma_j

3

4

0

基变量是

x_3

和

x_4

, 基变量在约束条件中的系数矩阵

\begin{bmatrix} &1 & 0 & \\\\ &0 & 1 & \end{bmatrix}

就是基矩阵 , 这是个单位阵 ;

基变量是

x_3

和

x_4

在目标函数中的系数是

\begin{pmatrix} \quad 0 \quad 0 \quad \end{pmatrix}

;

此时的基解是

\begin{pmatrix} \quad 0 \quad \\ \quad 0 \quad \\ \quad 40 \quad \\ \quad 30 \quad \\ \end{pmatrix}

, 该解是初始解 , 下面判定该解是否是最优解 ;

五、最优解判定

使用检验数矩阵

( C_N^T - C_B^T B^{-1}N )

判断上述解 , 是否是最优解 , 该矩阵计算结果中所有的数 , 都是检验数

\sigma

, 如果所有的数都小于等于

0

, 说明该解就是最优解 ;

这里只求非基变量的检验数 , 即

x_1

,

x_2

的检验数 ;

列出目标函数非基变量系数

( C_N^T - C_B^T B^{-1}N )

矩阵 :

非基变量在目标函数中的系数矩阵 :

C_N^T=\begin{pmatrix} \quad 3 \quad 4 \quad \end{pmatrix}

基变量在目标函数中的叙述矩阵 :

C_B^T = \begin{pmatrix} \quad 0 \quad 0 \quad \end{pmatrix}

B^{-1}N

是系数矩阵中经过矩阵变换后 , 基变量系数是单位阵

I

, 非基变量系数是

B^{-1}N

:

B^{-1}N =\begin{bmatrix} &2 & 1 & \\\\ &1 & 3 & \end{bmatrix}

( C_N^T - C_B^T B^{-1}N ) = C_N^T=\begin{pmatrix} \quad 3 \quad 4 \quad \end{pmatrix} - \begin{pmatrix} \quad 0 \quad 0 \quad \end{pmatrix} \times \begin{bmatrix} &2 & 1 & \\\\ &1 & 3 & \end{bmatrix}

= \begin{pmatrix} \quad \sigma_{1} \quad \sigma_{2} \quad \end{pmatrix}

其中

\sigma_{1}

是目标函数中

x_1

的系数 ,

\sigma_{2}

是目标函数中的

x_2

的系数 ;

如果上述两个系数都小于等于

0

, 那么当非基变量

X_N =\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}

取值为

0

时 , 目标函数取值最大 ;

系数的计算公式为 :

\sigma_j = c_j - \sum c_i a_{ij}

, 其中

c_j

对应的是非基变量在目标函数系数 ,

c_i

是基变量在目标函数中的系数 ,

a_{ij}

是

B^{-1}N

中的矩阵向量 , 代表一列 ;

\sigma_{1} = c_1 - ( c_3 a_{11} + c_4 a_{12} )

\sigma_{1} =3 - (0 \times 2) - (0 \times 1) = 3

, 是从下面的单纯形表中的如下位置提取的数值 ;

\sigma_{2} = c_2 - ( c_3 a_{21} + c_4 a_{22} )

\sigma_{2} =4 - (0 \times 1) - (0 \times 3) = 4

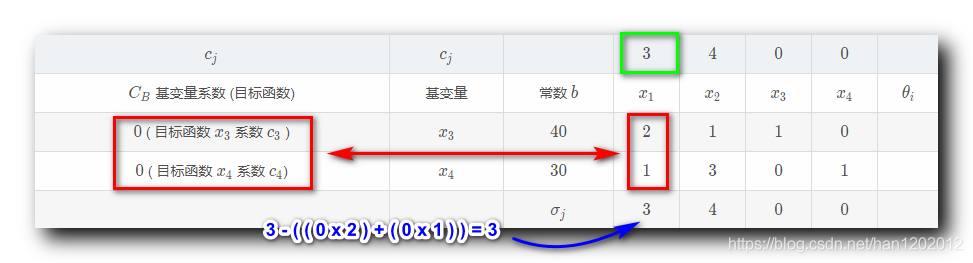
, 是从下面的单纯形表中的如下位置提取的数值 ;

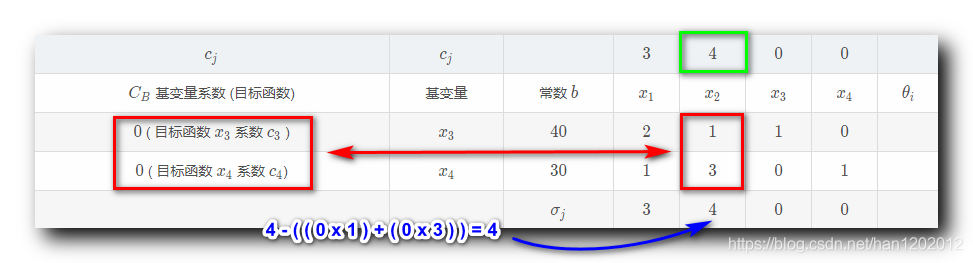
如果这两个系数 , 如果都小于等于

0

, 该基可行解

\begin{pmatrix} \quad 0 \quad \\ \quad 0 \quad \\ \quad 40 \quad \\ \quad 30 \quad \\ \end{pmatrix}

才是最优解 , 这两个系数都大于

0

, 因此不是最优解 ;

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2020-07-16，如有侵权请联系 cloudcommunity@tencent.com 删除

变量

博客

函数

本文分享自作者个人站点/博客前往查看

如有侵权，请联系 cloudcommunity@tencent.com 删除。

本文参与腾讯云自媒体同步曝光计划，欢迎热爱写作的你一起参与！

变量

博客

函数

登录后参与评论

0 条评论

热度