【运筹学】线性规划 人工变量法 ( 人工变量法案例 | 第一次迭代 | 中心元变换 | 检验数计算 | 选择入基变量 | 选择出基变量 )
【运筹学】线性规划 人工变量法 ( 人工变量法案例 | 第一次迭代 | 中心元变换 | 检验数计算 | 选择入基变量 | 选择出基变量 )

文章目录
- 一、第一次迭代 : 中心元变换
- 二、第一次迭代 : 单纯形表
- 三、第一次迭代 : 计算检验数
- 四、第一次迭代 : 最优解判定
- 五、第一次迭代 : 选择入基变量
- 六、第一次迭代 : 选择出基变量
- 七、第一次迭代 : 更新单纯形表
上一篇博客 【运筹学】线性规划 人工变量法 ( 人工变量法案例 | 初始单纯形表 | 检验数计算 | 入基变量 | 出基变量 ) 中 , 使用了人工变量法解没有单位阵的线性规划问题 , 通过添加人工变量 , 构造了单位阵 , 生成初始单纯形表 , 计算该单纯形表检验数 , 进行最优解判定 , 该初始基可行解不是最优解 , 先选择入基变量 , 然后根据入基变量选择出基变量 ; 本篇博客中开始进行第一次迭代计算 ;
一、第一次迭代 : 中心元变换
当前初始单纯形表 :
c j c_j cj | c j c_j cj | | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | |
|---|---|---|---|---|---|---|---|---|---|---|
C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
− M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
− M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
σ j \sigma_j σj ( 检验数 ) | | | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1 ) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2 ) | − 1 + 2 M -1 + 2M −1+2M ( σ 3 \sigma_3 σ3 ) | − M -M −M ( σ 4 \sigma_4 σ4 ) | 0 0 0 | 0 0 0 | 0 0 0 | |
基变量系数 (目标函数)
基变量常数
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 检验数 )
(
)
(
)
(
)
(
)
中心元 : 入基变量为
, 出基变量为
, 在单纯形表中 , 入基变量与出基变量相交的位置 , 称为中心元 ;
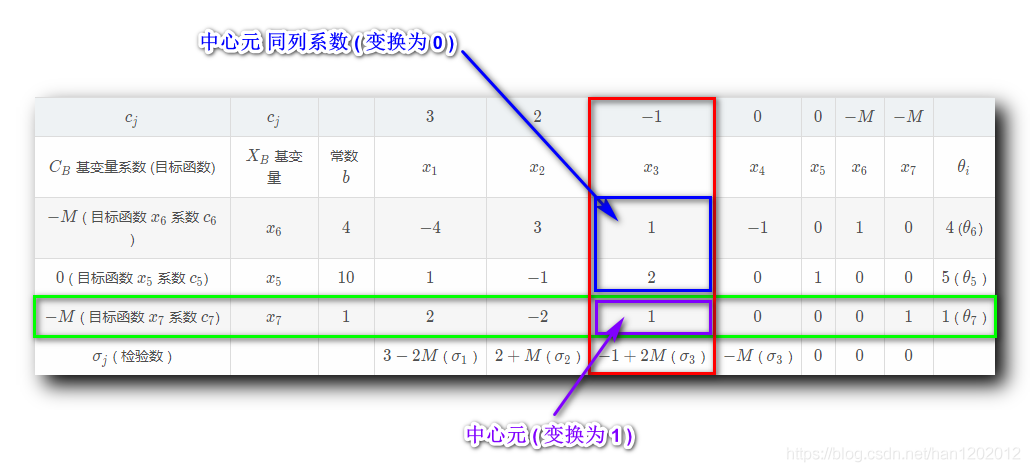
中心元变换 : 以中心元为轴 , 作系数矩阵变换 ;
- 中心元位置变换成
;
- 中心元对应入基变量所在列其它位置变换为
;
当前约束方程组为 :
方程
变换 : 在
中 ,
的系数是中心元 , 其系数需要变换成
, 其本身就是
, 方程
等式不用进行变换 ;
方程
变换 : 将
等式中
的系数变为
, 将 方程
左右两端乘以
, 与方程
相加 ;
方程
变换 : 将
等式中
的系数变为
, 将 方程
左右两端乘以
, 与方程
相加 ;
最终方程组为 :
二、第一次迭代 : 单纯形表
是后添加的人工变量 , 其取值肯定是
, 这里的单纯性表中 , 可以将
彻底删除 , 不再使用 ;
c j c_j cj | c j c_j cj | | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | |
|---|---|---|---|---|---|---|---|---|---|---|
C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
− M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
− M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
σ j \sigma_j σj ( 检验数 ) | | | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1 ) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2 ) | − 1 + 2 M -1 + 2M −1+2M ( σ 4 \sigma_4 σ4 ) | − M -M −M ( σ 3 \sigma_3 σ3 ) | 0 0 0 | 0 0 0 | 0 0 0 | |
第二次迭代 | – | – | – | – | – | – | – | – | – | – |
− M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 3 3 3 | − 6 -6 −6 | 5 5 5 | 0 0 0 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 移除 | ? ? ? ( θ 6 \theta_6 θ6) |
0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 8 8 8 | − 3 -3 −3 | 3 3 3 | 0 0 0 | 0 0 0 | 1 1 1 | 0 0 0 | 移除 | ? ? ? ( θ 5 \theta_5 θ5 ) |
− 1 -1 −1 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3) | x 3 x_3 x3 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 移除 | ? ? ? ( θ 3 \theta_3 θ3 ) |
σ j \sigma_j σj ( 检验数 ) | | | ? ? ? ( σ 1 \sigma_1 σ1 ) | ? ? ? ( σ 2 \sigma_2 σ2 ) | 0 0 0 | ? ? ? ( σ 4 \sigma_4 σ4 ) | 0 0 0 | 0 0 0 | 移除 | |
基变量系数 (目标函数)
基变量常数
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 检验数 )
(
)
(
)
(
)
(
)
第二次迭代––––––––––
( 目标函数
系数
)
移除
(
)
( 目标函数
系数
)
移除
(
)
( 目标函数
系数
)
移除
(
)
( 检验数 )
(
)
(
)
(
)
移除
三、第一次迭代 : 计算检验数
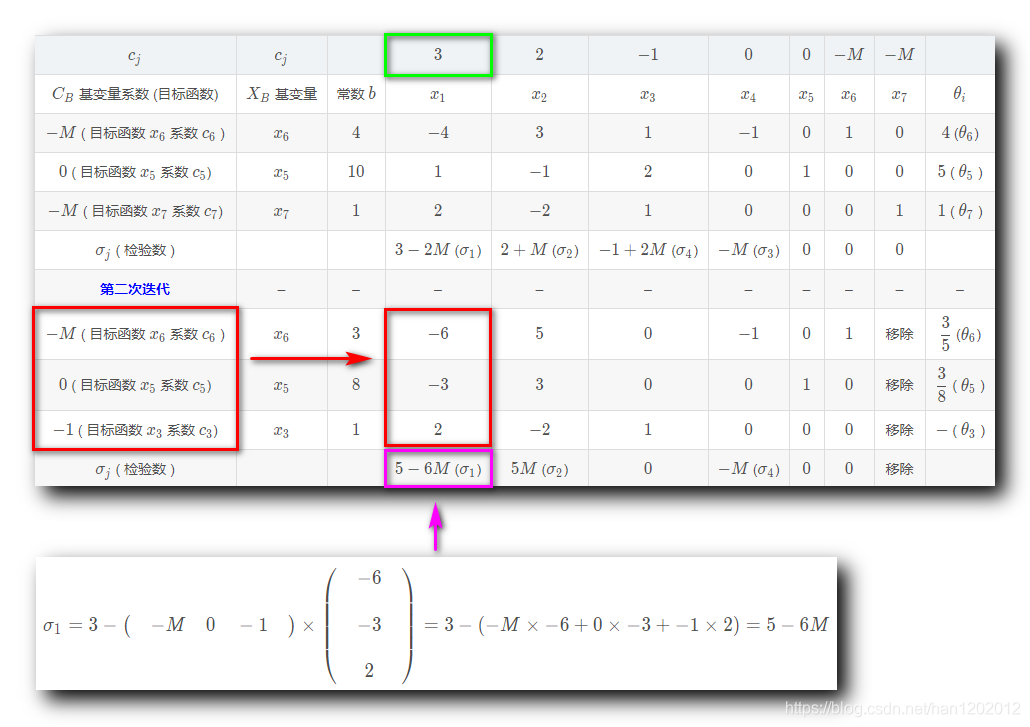
1 . 计算非基变量
的检验数
:
其中
是正无穷
,
是负数 ;
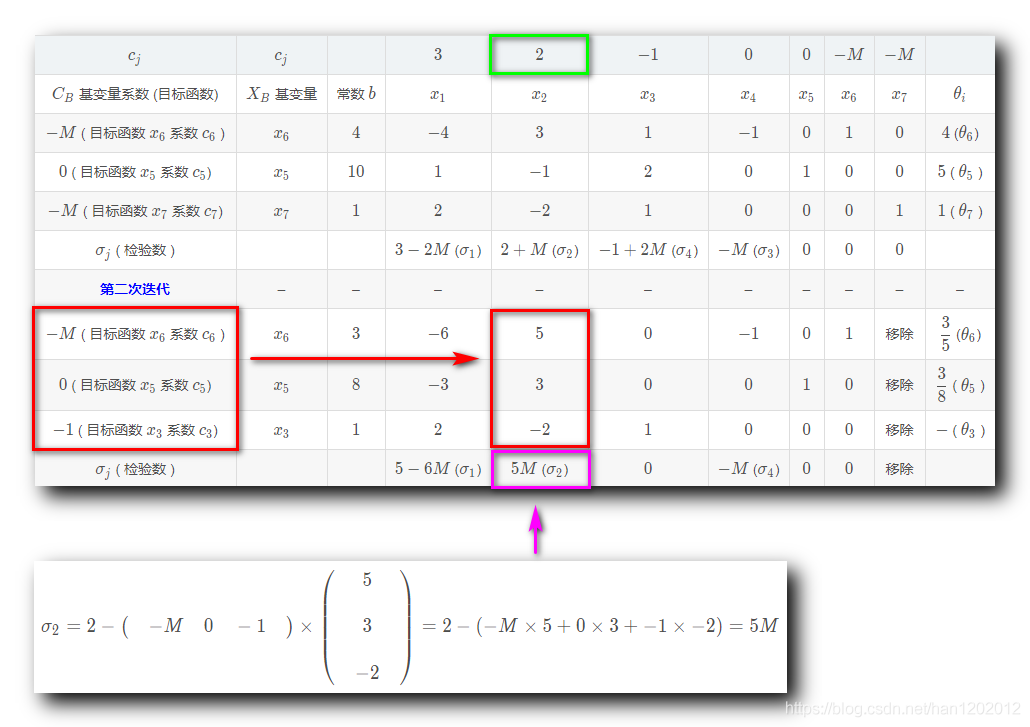
2 . 计算非基变量
的检验数
:
其中
是正无穷
,
是正数 ;
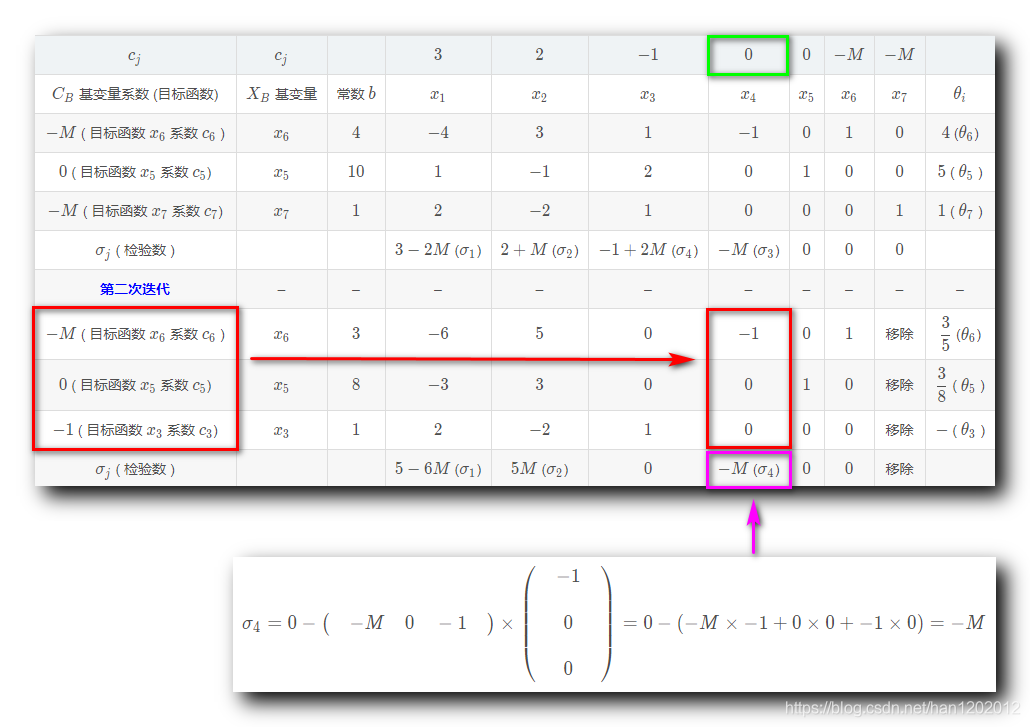
3 . 计算非基变量
的检验数
:
其中
是正无穷
,
是负数 ;
四、第一次迭代 : 最优解判定
根据上述三个检验数
的值 , 其中
检验数大于
, 该基可行解不是最优解 ;
只有当检验数都小于等于
时 , 该基可行解才是最优解 ;
五、第一次迭代 : 选择入基变量
根据上述三个检验数
的值 , 选择检验数最大的非基变量作为入基变量 ,
最大 , 这里选择
作为入基变量 ;
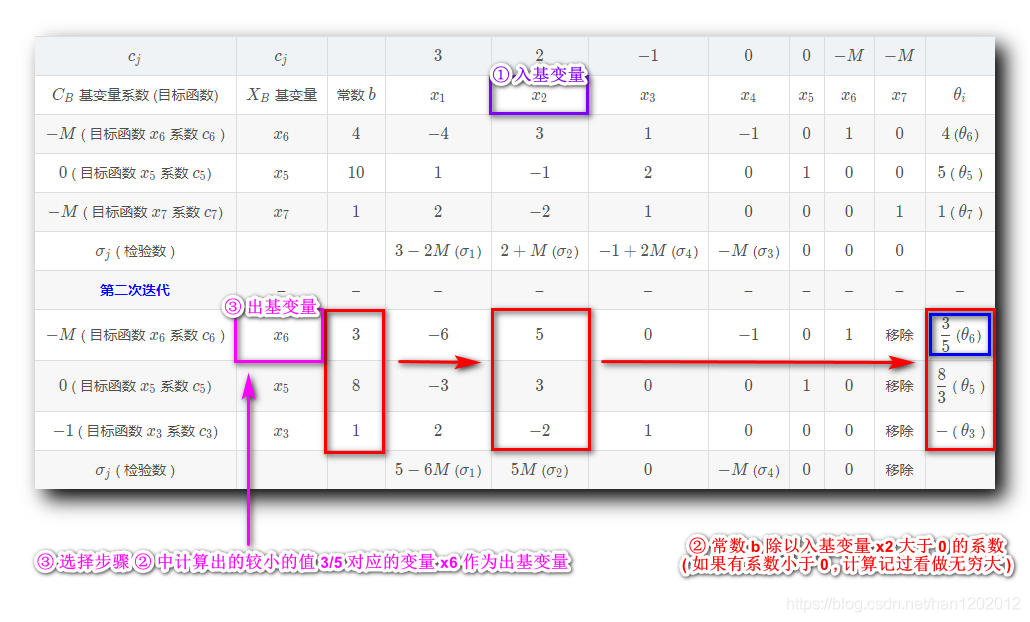
六、第一次迭代 : 选择出基变量
出基变量选择 : 常数列
, 分别除以除以入基变量
大于
的系数列
, 计算过程如下
, 得出结果是
, 如果系数小于等于
, 该值就是无效值 , 默认为无穷大 , 不进行比较 , 选择
对应的基变量作为出基变量 , 查看该最小值对应的变量是
, 选择该
变量作为出基变量 ;
七、第一次迭代 : 更新单纯形表
是后添加的人工变量 , 其取值肯定是
, 这里的单纯性表中 , 可以将
彻底删除 , 不再使用 ;
c j c_j cj | c j c_j cj | | 3 3 3 | 2 2 2 | − 1 -1 −1 | 0 0 0 | 0 0 0 | − M -M −M | − M -M −M | |
|---|---|---|---|---|---|---|---|---|---|---|
C B C_B CB 基变量系数 (目标函数) | X B X_B XB 基变量 | 常数 b b b | x 1 x_1 x1 | x 2 x_2 x2 | x 3 x_3 x3 | x 4 x_4 x4 | x 5 x_5 x5 | x 6 x_6 x6 | x 7 x_7 x7 | θ i \theta_i θi |
− M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 4 4 4 | − 4 -4 −4 | 3 3 3 | 1 1 1 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 0 0 0 | 4 4 4 ( θ 6 \theta_6 θ6) |
0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 10 10 10 | 1 1 1 | − 1 -1 −1 | 2 2 2 | 0 0 0 | 1 1 1 | 0 0 0 | 0 0 0 | 5 5 5 ( θ 5 \theta_5 θ5 ) |
− M -M −M ( 目标函数 x 7 x_7 x7 系数 c 7 c_7 c7) | x 7 x_7 x7 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 1 1 1 | 1 1 1 ( θ 7 \theta_7 θ7 ) |
σ j \sigma_j σj ( 检验数 ) | | | 3 − 2 M 3-2M 3−2M ( σ 1 \sigma_1 σ1) | 2 + M 2+M 2+M ( σ 2 \sigma_2 σ2) | − 1 + 2 M -1 + 2M −1+2M ( σ 4 \sigma_4 σ4) | − M -M −M ( σ 3 \sigma_3 σ3) | 0 0 0 | 0 0 0 | 0 0 0 | |
第二次迭代 | – | – | – | – | – | – | – | – | – | – |
− M -M −M ( 目标函数 x 6 x_6 x6 系数 c 6 c_6 c6 ) | x 6 x_6 x6 | 3 3 3 | − 6 -6 −6 | 5 5 5 | 0 0 0 | − 1 -1 −1 | 0 0 0 | 1 1 1 | 移除 | 3 5 \dfrac{3}{5} 53 ( θ 6 \theta_6 θ6) |
0 0 0 ( 目标函数 x 5 x_5 x5 系数 c 5 c_5 c5) | x 5 x_5 x5 | 8 8 8 | − 3 -3 −3 | 3 3 3 | 0 0 0 | 0 0 0 | 1 1 1 | 0 0 0 | 移除 | 8 3 \dfrac{8}{3} 38 ( θ 5 \theta_5 θ5 ) |
− 1 -1 −1 ( 目标函数 x 3 x_3 x3 系数 c 3 c_3 c3) | x 3 x_3 x3 | 1 1 1 | 2 2 2 | − 2 -2 −2 | 1 1 1 | 0 0 0 | 0 0 0 | 0 0 0 | 移除 | − - − ( θ 3 \theta_3 θ3 ) |
σ j \sigma_j σj ( 检验数 ) | | | 5 − 6 M 5-6M 5−6M ( σ 1 \sigma_1 σ1) | 5 M 5M 5M ( σ 2 \sigma_2 σ2) | 0 0 0 | − M -M −M ( σ 4 \sigma_4 σ4) | 0 0 0 | 0 0 0 | 移除 | |
基变量系数 (目标函数)
基变量常数
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 目标函数
系数
)
(
)
( 检验数 )
(
)
(
)
(
)
(
)
第二次迭代––––––––––
( 目标函数
系数
)
移除
(
)
( 目标函数
系数
)
移除
(
)
( 目标函数
系数
)
移除
(
)
( 检验数 )
(
)
(
)
(
)
移除

