第十一届蓝桥杯大赛软件类决赛 C++ B组 题解

声明：本人水平有限，只是个人的见解，如果有更好的答案，欢迎评论区或者私信我，我会注明您的题解来源，谢谢支持！

本文是2020年11月14日的蓝桥杯全国总决赛  软件类 C B组题解

本文原创首发CSDN，本文链接https://blog.csdn.net/qq_41464123/article/details/109695384 ，作者博客https://zwz99.blog.csdn.net/ ，转载请带上本链接，谢谢配合。

试题 A: 美丽的 2

本题总分：5 分

我的答案：563，水题暴力循环即可

【问题描述】

小蓝特别喜欢 2，今年是公元 2020 年，他特别高兴。

他很好奇，在公元 1 年到公元 2020 年（包含）中，有多少个年份的数位中 包含数字 2？

int fx(int x) {
	int num = 0;
	while (x > 0) {
		if (x % 10 == 2) {
			num++;
		}
		x /= 10;
	}
	return num;
}
int main() {
	int ans = 0;
	for (int i = 1; i <= 2020; i++) {
		if (fx(i) > 0) ans++;
	}
	cout << ans << endl;
	return 0;
}

试题 B: 扩散

本题总分： 5 分

等待大神认领

【问题描述】

小蓝在一张无限大的特殊画布上作画。 这张画布可以看成一个方格图，每个格子可以用一个二维的整数坐标表示。 小蓝在画布上首先点了一下几个点：(0 , 0) , (2020 , 11) , (11 , 14) , (2000 , 2000) 。 只有这几个格子上有黑色，其它位置都是白色的。

每过一分钟，黑色就会扩散一点。具体的，如果一个格子里面是黑色，它就会扩散到上、下、左、右四个相邻的格子中，使得这四个格子也变成黑色 （如果原来就是黑色，则还是黑色）。

请问，经过 2020 分钟后，画布上有多少个格子是黑色的。

试题 C: 阶乘约数

我的答案：883423532389192164791648750371459257913741948437809479060803100646309888

我的思路是先求出1到100所有数的质因子，共239个，然后C(0,239)+C(1,239)+C(2,239)+...+C(238,239)+C(239,239) 就等于2的239次

本题总分： 10 分

【问题描述】

定义阶乘 n ! = 1 × 2 × 3 × · · · × n 。

请问 100! （ 100 的阶乘）有多少个约数。

bool ssbiao[102];
int num[102];
bool ss(int x) {
	if (x < 2) return false;
	for (int i = 2; i < x; i++) {
		if (x % i == 0) return false;
	}
	return true;
}
void init() {
	int ansSum = 0;
	for (int i = 2; i < 100; i++) {
		if (ss(i)) ssbiao[i] = true;
	}
	for (int i = 2; i <= 100; i++) {
		int j = i;
		while (j > 1) {
			for (int k = 2; k < 100; k++) {
				if (ssbiao[k] && (j % k == 0)) {
					j /= k;
					num[k] ++;
					ansSum++;
				}
			}
		}
	}
	for (int i = 2; i <= 100; i++) {
		cout << i << " : " << num[i] << endl;
	}
	cout << ansSum << endl;
}
int main() {
	// init();
	double s = pow(2.0, 239.0);
	printf("%lf\n", s);
	cout << s << endl;
	//883423532389192164791648750371459257913741948437809479060803100646309888
	return 0;
}

试题 D: 本质上升序列

本题总分：10 分

​​​​​​​等待大神认领

【问题描述】

小蓝特别喜欢单调递增的事物。在一个字符串中，如果取出若干个字符，将这些字符按照在字符串中的顺 序排列后是单调递增的，则成为这个字符串中的一个单调递增子序列。

例如，在字符串 lanqiao 中，如果取出字符 n 和 q ，则 nq 组成一个单 调递增子序列。类似的单调递增子序列还有 lnq 、 i 、 ano 等等。 小蓝发现，有些子序列虽然位置不同，但是字符序列是一样的，例如取第 二个字符和最后一个字符可以取到 ao ，取最后两个字符也可以取到 ao 。小蓝 认为他们并没有本质不同。

对于一个字符串，小蓝想知道，本质不同的递增子序列有多少个？

例如，对于字符串 lanqiao ，本质不同的递增子序列有 21 个。它们分别 是 l 、 a 、 n 、 q 、 i 、 o 、 ln 、 an 、 lq 、 aq 、 nq 、 ai 、 lo 、 ao 、 no 、 io 、 lnq 、 anq、 lno 、 ano 、 aio 。

请问对于以下字符串（共 200 个小写英文字母，分四行显示）

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf

iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij

gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad

vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

本质不同的递增子序列有多少个？

试题 E: 玩具蛇

我的答案：604，从每一个点开始深搜，搜到给标记，退回还原标记，16个点结果相加就是604

本题总分：15 分

【问题描述】

小蓝有一条玩具蛇，一共有 16 节，上面标着数字 1 至 16 。每一节都是一 个正方形的形状。相邻的两节可以成直线或者成 90 度角。 小蓝还有一个 4 × 4 的方格盒子，用于存放玩具蛇，盒子的方格上依次标着 字母 A 到 P 共 16 个字母。

小蓝可以折叠自己的玩具蛇放到盒子里面。他发现，有很多种方案可以将 玩具蛇放进去。

下图给出了两种方案：

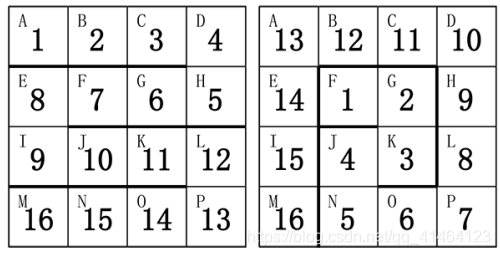
请帮小蓝计算一下，总共有多少种不同的方案。如果两个方案中，存在玩

具蛇的某一节放在了盒子的不同格子里，则认为是不同的方案。

int a[5][5];
bool b[5][5];
int ans = 0;
void init() {
	for (int i = 0; i < 5; i++) {
		for (int j = 0; j < 5; j++) {
			a[i][j] = 0;
			b[i][j] = false;
		}
	}
}
void dfs(int x, int y, int num) {
	if (x < 0 || x >3 || y < 0 || y > 3) return;
	if (b[x][y]) return;
	if (num == 16) {
		ans++;
		return;
	}
	b[x][y] = true;
	dfs(x, y + 1, num + 1);
	dfs(x, y - 1, num + 1);
	dfs(x + 1, y, num + 1);
	dfs(x - 1, y, num + 1);
	b[x][y] = false;
}
int main() {
	ans = 0;
	dfs(0, 0, 1);
	for (int i = 0; i < 4; i++) {
		for (int j = 0; j < 4; j++) {
			init();
			dfs(i, j, 1);
		}
	}
	cout << ans << endl;// 604
}

本文原创首发CSDN，本文链接https://blog.csdn.net/qq_41464123/article/details/109695384 ，作者博客https://zwz99.blog.csdn.net/ ，转载请带上本链接，谢谢配合。

试题 F: 皮亚诺曲线距离

我的思路：

首先对于这样的图形，只有两个图案，我们认定最左下角的那块坐标为（0,0） 那么当x坐标加y坐标为偶数时，是第一种图形 当x坐标加y坐标为奇数时，是第二种图形 不管是第一种图形还是第二种图形，都有入口和出口 并且每一个点到入口的路径是确定的 第一种图形到入口的路径由fx1()求，第二种由fx2()求 求任意两个点，首先要确定在哪两个大块 比如阶数为3的样例，可以看做9个9*9的二阶大块构成，求出相距几个大块 接下来把一个大块平移到另外一个大块，注意平移的是到入口的路径 接下来求二阶，看做9个3*3的样例构成，一直递归下去......

【问题描述】

皮亚诺曲线是一条平面内的曲线。 下图给出了皮亚诺曲线的 1 阶情形，它是从左下角出发，经过一个 3 × 3 的 方格中的每一个格子，最终到达右上角的一条曲线。

下图给出了皮亚诺曲线的 2 阶情形，它是经过一个 3 2 × 3 2 的方格中的每一 个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。

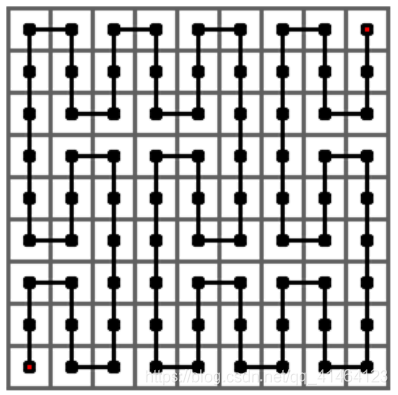
下图给出了皮亚诺曲线的 3 阶情形，它是经过一个 3 3 × 3 3 的方格中的每一 个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发，最终到达右上角。 我们将这些格子放到坐标系中，对于 k 阶皮亚诺曲线，左下角的坐标是 (0, 0) ，右上角坐标是 (3 k - 1 , 3 k - 1) ，右下角坐标是 (3 k - 1 , 0) ，左上角坐标是 (0, 3 k - 1) 。

给定 k 阶皮亚诺曲线上的两个点的坐标，请问这两个点之间，如果沿着皮亚诺曲线走，距离是到少？

【输入格式】

输入的第一行包含一个正整数 k ，皮亚诺曲线的阶数。

第二行包含两个整数 x 1 , y 1 ，表示第一个点的坐标。

第三行包含两个整数 x 2 , y 2 ，表示第二个点的坐标。

【输出格式】

输出一个整数，表示给定的两个点之间的距离。

【样例输入】

1

0 0

2 2

【样例输出】

8

【样例输入】

2

0 2

0 3

【样例输出】

13

【评测用例规模与约定】

对于 30 % 的评测用例， 0 ≤ k ≤ 10 。

对于 50 % 的评测用例， 0 ≤ k ≤ 20 。

对于所有评测用例， 0 ≤ k ≤ 100 , 0 ≤ x 1 , y 1 , x 2 , y 2 < 3 k , x 1 , y 1 , x 2 , y 2 ≤ 10 18 。

数据保证答案不超过 10 18 。

int fx1(int x,int y) {
	if (x == 0 && y == 0) return 1;
	if (x == 0 && y == 1) return 2;
	if (x == 0 && y == 2) return 3;
	if (x == 1 && y == 2) return 4;
	if (x == 1 && y == 1) return 5;
	if (x == 1 && y == 0) return 6;
	if (x == 2 && y == 0) return 7;
	if (x == 2 && y == 1) return 8;
	if (x == 2 && y == 2) return 9;
	return 0;
}
int fx2(int x, int y) {
	if (x == 2 && y == 0) return 9;
	if (x == 2 && y == 1) return 8;
	if (x == 2 && y == 2) return 7;
	if (x == 1 && y == 2) return 6;
	if (x == 1 && y == 1) return 5;
	if (x == 1 && y == 0) return 4;
	if (x == 0 && y == 0) return 3;
	if (x == 0 && y == 1) return 2;
	if (x == 0 && y == 2) return 1;
	return 0;
}
int jl(int x, int y,int x1,int y1) {
	if (x < 3 && y < 3 && x1 < 3 && y1 < 3)
		return fx1(x, y) - fx1(x1, y1);
	return jl(x / 3, y / 3, x1 / 3, y1 / 3);
}
int main() {
	
	int jie;
	while (cin >> jie) {
		int scanfJie = jie;
		int x1, y1, x2, y2;
		int xx1, yy1, xx2, yy2;
		cin >> x1 >> y1;
		cin >> x2 >> y2;
		int scanfX1 = x1;
		int scanfX2 = x2;
		int scanfY1 = y1;
		int scanfY2 = y2;
		int da1, da2;
		int ans = 0;
		
		while (jie > 1) {
			int tempJie = (int)pow(3, jie - 1);
			xx1 = scanfX1 / tempJie;
			yy1 = scanfY1 / tempJie;
			xx2 = scanfX2 / tempJie;
			yy2 = scanfY2 / tempJie;
			da1 = fx1(xx1, yy1);
			da2 = fx1(xx2, yy2);
			ans *= 9;
			ans += da2 - da1;
			scanfX1 %= tempJie;
			scanfX2 %= tempJie;
			scanfY1 %= tempJie;
			scanfY2 %= tempJie;
			jie--;
		}
		ans *= 9;
		int xx = x1 / 3;
		int yy = y1 / 3;
		int type1, type2;
		int num1, num2;
		if ((xx + yy) % 2 == 0) {
			type1 = 1;
			num1 = fx1(x1 % 3, y1 % 3);
		}
		else {
			type1 = 2;
			num1 = fx2(x1 % 3, y1 % 3);
		}
		
		xx = x2 / 3;
		yy = y2 / 3;
		if ((xx + yy) % 2 == 0) {
			type2 = 1;
			num2 = fx1(x2 % 3, y2 % 3);
		}
		else {
			type2 = 2;
			num2 = fx2(x2 % 3, y2 % 3);
		}
		ans += num2 - num1;
		// cout << num1 << "   " << num2 << endl;
		cout << ans << endl;
	}
	return 0;
}

试题 G: 游园安排

本题总分： 20 分

我的思路： 这题就是最长上升子序列 首先把单词分割开来，给定每个单词一个排序值，再求这个排序值数组的最长上升子序列 算法模板忘记咋写了，所以自己暴力模拟的，思路很暴躁

【问题描述】

L 星球游乐园非常有趣，吸引着各个星球的游客前来游玩。小蓝是 L 星球 游乐园的管理员。 为了更好的管理游乐园，游乐园要求所有的游客提前预约，小蓝能看到系 统上所有预约游客的名字。每个游客的名字由一个大写英文字母开始，后面跟 0 个或多个小写英文字母。游客可能重名。 小蓝特别喜欢递增的事物。今天，他决定在所有预约的游客中，选择一部 分游客在上午游玩，其他的游客都在下午游玩，在上午游玩的游客要求按照预 约的顺序排列后，名字是单调递增的，即排在前面的名字严格小于排在后面的 名字。

一个名字 A 小于另一个名字 B 是指：存在一个整数 i ，使得 A 的前 i 个字 母与 B 的前 i 个字母相同，且 A 的第 i + 1 个字母小于 B 的第 i + 1 个字母。（如 果 A 不存在第 i + 1 个字母且 B 存在第 i + 1 个字母，也视为 A 的第 i + 1 个字 母小于 B 的第 i + 1 个字母）

作为小蓝的助手，你要按照小蓝的想法安排游客，同时你又希望上午有尽 量多的游客游玩，请告诉小蓝让哪些游客上午游玩。如果方案有多种，请输出上午游玩的第一个游客名字最小的方案。如果此时还有多种方案，请输出第一 个游客名字最小的前提下第二个游客名字最小的方案。如果仍然有多种，依此类推选择第三个、第四个……游客名字最小的方案。

【输入格式】

输入包含一个字符串，按预约的顺序给出所有游客的名字，相邻的游客名

字之间没有字符分隔。

【输出格式】

按预约顺序输出上午游玩的游客名单，中间不加任何分隔字符。

【样例输入】

WoAiLanQiaoBei

【样例输出】

AiLanQiao

【评测用例规模与约定】

对于 20 % 的评测数据，输入的总长度不超过 20 个字母。

对于 50 % 的评测数据，输入的总长度不超过 300 个字母。

对于 70 % 的评测数据，输入的总长度不超过 10000 个字母。

对于所有评测数据，每个名字的长度不超过 10 个字母，输入的总长度不超

过 1000000 个字母。

string scanfString[10000];
string sortString[10000];
int rankString[10000];
int num;
int ansUp[10000];
int ansLen;
int anssUp[10000];
int anssLen;
// 求最长上升子序列
void calMaxUpSonArray() {
	ansLen = 1;
	ansUp[0] = rankString[0];
	anssLen = 1;
	anssUp[0] = rankString[0];
	for (int k = 0; k < num; k++) {
		ansLen = 1;
		ansUp[0] = rankString[k];
		for (int i = k + 1; i < num; i++) {
			if (rankString[i] < ansUp[ansLen - 1] && (ansLen == 1 || ansLen > 1 && rankString[i] >= ansUp[ansLen - 2])) {
				ansUp[ansLen - 1] = rankString[i];
			}
			else if (rankString[i] >= ansUp[ansLen - 1]) {
				ansUp[ansLen] = rankString[i];
				ansLen++;
			}
		}
		if (ansLen < anssLen) break;
		else if (ansLen > anssLen) {
			anssLen = ansLen;
			for (int i = 0; i < ansLen; i++) {
				anssUp[i] = ansUp[i];
			}
		}
		else {
			bool flag = true;
			for (int i = 0; i < ansLen; i++) {
				if (ansUp[i] > anssUp[i]) {
					flag = false;
					break;
				}
			}
			if (flag) {
				for (int i = 0; i < ansLen; i++) {
					anssUp[i] = ansUp[i];
				}
			}
		}
	}
	for (int i = 0; i < anssLen; i++) {
		for (int j = 0; j < num; j++) {
			if (rankString[j] == anssUp[i]) {
				cout << scanfString[j];
				break;
			}
		}
	}
	cout << endl;
}
int main() {
	string str;
	while (cin >> str) {
		num = 0;
		string temp;
        // 字符分解
		for (int i = 0; i < str.length(); i++) {
			if (str[i] >= 'A' && str[i] <= 'Z' && i > 0) {
				scanfString[num] = temp;
				sortString[num++] = temp;
				temp = "";
			}
			temp += str[i];
		}
		scanfString[num] = temp;
		sortString[num++] = temp;
		sort(sortString, sortString + num);
        // 排序后名次给rankString数组
		for (int i = 0; i < num; i++) { // scanfString
			for (int j = 0; j < num; j++) { // sortString
				if (scanfString[i]._Equal(sortString[j])) {
					rankString[i] = j;
					break;
				}
			}
		}
		// 求最长上升子序列
		calMaxUpSonArray();
	}
	return 0;
}

试题 H: 答疑

本题总分： 20 分

我的思路： 进入办公室的时间和答疑的时间可以看做一个整体 贪心，优先看总时间最少的，其次看答疑速度快的 比如进办公室+答疑时间5秒，离开5秒，肯定比 进办公室+答疑时间6秒，离开4秒划算 比如进办公室+答疑时间6秒，离开4秒，肯定比 进办公室+答疑时间4秒，离开7秒划算

【问题描述】

有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。 老师可以安排答疑的顺序，同学们要依次进入老师办公室答疑。

一位同学答疑的过程如下：

1. 首先进入办公室，编号为 i 的同学需要 s i 毫秒的时间。

2. 然后同学问问题老师解答，编号为 i 的同学需要 a i 毫秒的时间。

3. 答疑完成后，同学很高兴，会在课程群里面发一条消息，需要的时间可以忽略。

4. 最后同学收拾东西离开办公室，需要 e i 毫秒的时间。一般需要 10 秒、 20 秒或 30 秒，即 e i 取值为 10000 ， 20000 或 30000 。

一位同学离开办公室后，紧接着下一位同学就可以进入办公室了。 答疑从 0 时刻开始。老师想合理的安排答疑的顺序，使得同学们在课程群 里面发消息的时刻之和最小。

【输入格式】

输入第一行包含一个整数 n ，表示同学的数量。

接下来 n 行，描述每位同学的时间。其中第 i 行包含三个整数 s i , a i , e i ，意

义如上所述。

【输出格式】

输出一个整数，表示同学们在课程群里面发消息的时刻之和最小是多少。

【样例输入】

3

10000 10000 10000

20000 50000 20000

30000 20000 30000

【样例输出】

280000

【样例说明】

按照 1 , 3 , 2 的顺序答疑，发消息的时间分别是 20000 , 80000 , 180000 。

【评测用例规模与约定】

对于 30 % 的评测用例， 1 ≤ n ≤ 20 。

对于 60 % 的评测用例， 1 ≤ n ≤ 200 。

对于所有评测用例， 1 ≤ n ≤ 1000 ， 1 ≤ s i ≤ 60000 ， 1 ≤ a i ≤ 1000000 ，

e i ∈ { 10000 , 20000 , 30000 } ，即 e i 一定是 10000 、 20000 、 30000 之一。

struct ss {
	long long a;
	long long b;
}peo[1002];
bool cmp(ss a, ss b) {
	if ((a.a + a.b) != (b.a + b.b)) {
		return (a.a + a.b) < (b.a + b.b);
	}
	return a.b > b.b;
}
int main() {
	int n;
	while (cin >> n) {
		for (int i = 0; i < n; i++) {
			long long aa, bb, cc;
			cin >> aa >> bb >> cc;
			peo[i].a = aa + bb;
			peo[i].b = cc;
		}
		sort(peo, peo + n, cmp);
		long long ans = 0;
		long long nowTimes = 0;
		for (int i = 0; i < n; i++) {
			nowTimes += peo[i].a;
			ans += nowTimes;
			nowTimes += peo[i].b;
		}
		cout << ans << endl;
	}
	return 0;
}

试题 I: 出租车

本题总分： 25 分

等待大神认领

【问题描述】

小蓝在 L 市开出租车。 L 市的规划很规整，所有的路都是正东西向或者正南北向的，道路都可以 看成直线段。东西向的道路互相平行，南北向的道路互相平行，任何一条东西 向道路垂直于任何一条南北向道路。

从北到南一共有 n 条东西向道路，依次标号为 H 1 , H 2 , · · · , H n 。从西到东一共有 m 条南北向的道路，依次标号为 S 1 , S 2 , · · · , S m 。 每条道路都有足够长，每一条东西向道路和每一条南北向道路都相交，H i 与 S j 的交叉路口记为 ( i , j ) 。 从 H 1 和 S 1 的交叉路口 (1 , 1) 开始，向南遇到的路口与 (1 , 1) 的距离分别 是 h 1 , h 2 , · · · , h nn 1 ，向东遇到路口与 (1 , 1) 的距离分别是 w 1 , w 2 , · · · , w mm 1 。 道路的每个路口都有一个红绿灯。

时刻 0 的时候，南北向绿灯亮，东西向红灯亮，南北向的绿灯会持续一段 时间（每个路口不同），然后南北向变成红灯，东西向变成绿灯，持续一段时间 后，再变成南北向绿灯，东西向红灯。 已知路口 ( i , j ) 的南北向绿灯每次持续的时间为 g i j ，东西向的绿灯每次持 续的时间为 r i j ，红绿灯的变换时间忽略。 当一辆车走到路口时，如果是绿灯，可以直行、左转或右转。如果是红灯， 可以右转，不能直行或左转。如果到路口的时候刚好由红灯变为绿灯，则视为 看到绿灯，如果刚好由绿灯变为红灯，则视为看到红灯。 每段道路都是双向道路，道路中间有隔离栏杆，在道路中间不能掉头，只 能在红绿灯路口掉头。掉头时不管是红灯还是绿灯都可以直接掉头。掉头的时间可以忽略。

小蓝时刻 0 从家出发。今天，他接到了 q 个预约的订单，他打算按照订单 的顺序依次完成这些订单，就回家休息。中途小蓝不准备再拉其他乘客。

小蓝的家在两个路口的中点，小蓝喜欢用 x 1 , y 1 , x 2 , y 2 来表示自己家的位 置，即路口 ( x 1 , y 1 ) 到路口 ( x 2 , y 2 ) 之间的道路中点的右侧，保证两个路口相邻 （中间没有其他路口）。请注意当两个路口交换位置时，表达的是路的不同两边， 路中间有栏杆，因此这两个位置实际要走比较远才能到达。 小蓝的订单也是从某两个路口间的中点出发，到某两个路口间的中点结束。

小蓝必须按照给定的顺序处理订单，而且一个时刻只能处理一个订单，不能图 省时间而同时接两位乘客，也不能插队完成后面的订单。

小蓝只对 L 市比较熟，因此他只会在给定的 n 条东西向道路和 m 条南北向 道路上行驶，而且不会驶出 H 1 , H n , S 1 , S m 这几条道路所确定的矩形区域（可 以到边界）。

小蓝行车速度一直为 1 ，乘客上下车的时间忽略不计。

请问，小蓝最早什么时候能完成所有订单回到家。

【输入格式】

输入第一行包含两个整数 n , m ，表示东西向道路的数量和南北向道路的数 量。

第二行包含 n n 1 个整数 h 1 , h 2 , · · · , h nn 1 。

第三行包含 m m 1 个整数 w 1 , w 2 , · · · , w mm 1 。

接下来 n 行，每行 m 个整数，描述每个路口南北向绿灯的时间，其中的第 i 行第 j 列表示 g i j 。

接下来 n 行，每行 m 个整数，描述每个路口东西向绿灯的时间，其中的第 i 行第 j 列表示 r i j 。

接下来一行包含四个整数 x 1 , y 1 , x 2 , y 2 ，表示小蓝家的位置在路口 ( x 1 , y 1 ) 到路口 ( x 2 , y 2 ) 之间的道路中点的右侧。

接下来一行包含一个整数 q ，表示订单数量。

接下来 q 行，每行描述一个订单，其中第 i 行包含八个整数 x i 1 , y i 1 , x i 2 , y i 2 , x i 3 , y i 3 , x i 4 , y i 4 ，表示第 i 个订单的起点为路口 ( x i 1 , y i 1 ) 到路口 ( x i 2 , y i 2 ) 之间的道 路中点的右侧，第 i 个订单的终点为路口 ( x i 3 , y i 3 ) 到路口 ( x i 4 , y i 4 ) 之间的道路中 点的右侧。

【输出格式】

输出一个实数，表示小蓝完成所有订单最后回到家的最早时刻。四舍五入

保留一位小数。

【样例输入】

2 3

200

100 400

10 20 10

20 40 30

20 20 20

20 20 20

2 1 1 1

1

2 2 1 2 1 2 1 3

【样例输出】

1620.0

【样例说明】

小蓝有一个订单，他的行车路线如下图所示。其中 H 表示他家的位置， S

表示订单的起点， T 表示订单的终点。小明在最后回家时要在直行的红绿灯路

口等绿灯，等待时间为 20 。

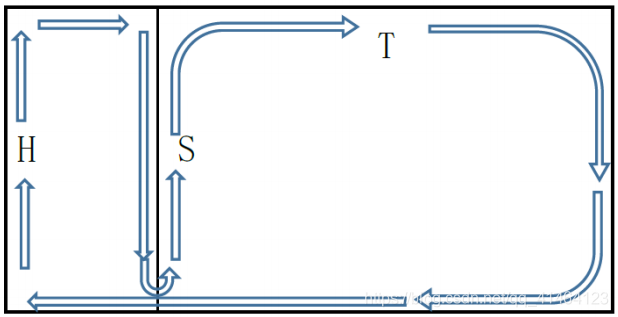
【评测用例规模与约定】

对于 20 % 的评测用例， 1 ≤ n , m ≤ 5 ， 1 ≤ q ≤ 10 。

对于 50 % 的评测用例， 1 ≤ n , m ≤ 30 ， 1 ≤ q ≤ 30 。

对于所有评测用例， 1 ≤ n , m ≤ 100 ， 1 ≤ q ≤ 30 ， 1 ≤ h 1 < h 2 < · · · < h nn 1 ≤ 100000， 1 ≤ w 1 < w 2 < · · · < w mm 1 ≤ 100000 ， 1 ≤ g i j ≤ 1000 ， 1 ≤ r i j ≤ 1000 ，给 定的路口一定合法。

试题 J: 质数行者

本题总分： 25 分

​​​​​​​等待大神认领

【问题描述】

小蓝在玩一个叫质数行者的游戏。 游戏在一个 n × m × w 的立体方格图上进行，从北到南依次标号为第 1 行到 第 n 行，从西到东依次标号为第 1 列到第 m 列，从下到上依次标号为第 1 层到 第 w 层。

小蓝要控制自己的角色从第 1 行第 1 列第 1 层移动到第 n 行第 m 列第 w 层。每一步，他可以向东走质数格、向南走质数格或者向上走质数格。每走到 一个位置，小蓝的角色要稍作停留。 在游戏中有两个陷阱，分别为第 r 1 行第 c 1 列第 h 1 层和第 r 2 行第 c 2 列第 h 2 层。这两个陷阱的位置可以跨过，但不能停留。也就是说，小蓝不能控制角 色某一步正好走到陷阱上，但是某一步中间跨过了陷阱是允许的。 小蓝最近比较清闲，因此他想用不同的走法来完成这个游戏。所谓两个走法不同，是指小蓝稍作停留的位置集合不同。

请帮小蓝计算一下，他总共有多少种不同的走法。

提示：请注意内存限制，如果你的程序运行时超过内存限制将不得分。

【输入格式】

输入第一行包含两个整数 n , m , w ，表示方格图的大小。

第二行包含 6 个整数， r 1 , c 1 , h 1 , r 2 , c 2 , h 2 ，表示陷阱的位置。

【输出格式】

输出一行，包含一个整数，表示走法的数量。答案可能非常大，请输出答 案除以 1000000007 的余数。

【样例输入】

5 6 1

3 4 1 1 2 1

【样例输出】

11

【样例说明】

用 ( r , c , h ) 表示第 r 行第 c 列第 h 层，可能的走法有以下几种：

1. (1 , 1 , 1) ) (1 , 3 , 1) ) (1 , 6 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

2. (1 , 1 , 1) ) (1 , 3 , 1) ) (3 , 3 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

3. (1 , 1 , 1) ) (1 , 3 , 1) ) (3 , 3 , 1) ) (5 , 3 , 1) ) (5 , 6 , 1) 。

4. (1 , 1 , 1) ) (3 , 1 , 1) ) (3 , 3 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

5. (1 , 1 , 1) ) (3 , 1 , 1) ) (3 , 3 , 1) ) (5 , 3 , 1) ) (5 , 6 , 1) 。

6. (1 , 1 , 1) ) (3 , 1 , 1) ) (5 , 1 , 1) ) (5 , 3 , 1) ) (5 , 6 , 1) 。

7. (1 , 1 , 1) ) (3 , 1 , 1) ) (5 , 1 , 1) ) (5 , 4 , 1) ) (5 , 6 , 1) 。

8. (1 , 1 , 1) ) (1 , 4 , 1) ) (1 , 6 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

9. (1 , 1 , 1) ) (1 , 6 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

10. (1 , 1 , 1) ) (3 , 1 , 1) ) (3 , 6 , 1) ) (5 , 6 , 1) 。

11. (1 , 1 , 1) ) (3 , 1 , 1) ) (5 , 1 , 1) ) (5 , 6 , 1) 。

【评测用例规模与约定】

对于 30 % 的评测用例 1 ≤ n , m , w ≤ 50 。

对于 60 % 的评测用例 1 ≤ n , m , w ≤ 300 。

对于所有评测用例， 1 ≤ n , m , w ≤ 1000 ， 1 ≤ r 1 , r 2 ≤ n , 1 ≤ c 1 , c 2 ≤ m ,

1 ≤ h 1 , h 2 ≤ w ，陷阱不在起点或终点，两个陷阱不同。