visualgo学习与使用

前言：在反反复复学习数据结构和算法的过程中“邂逅”了visualgo----这款超级棒的学习网站。喜悦之情不亚于我以前玩前端时发现codepen时的快乐。

地址：https://visualgo.net/en

visualgo是新加坡国立大学计算机学院一位很棒的博士老师Dr. Steven Halim 在2011年写的一个可视化数据结构和计算机常用算法的开源项目，虽然现在没有维护了，但不可否认他依旧是一个很棒的网站。它最初的目的是为了帮助他的学生更好地理解算法和数据结构，但随着时间的推移，它已经成为了一个广受欢迎的在线教育工具。

Visualgo提供了各种算法和数据结构的可视化演示，包括排序、图形算法、字符串匹配和树等。这个平台的目标是让计算机科学变得更易于理解和互动。

他主要包含了24种常见算法问题：

1. 排序
2. 位掩码
3. 链表
4. 二叉堆
5. 哈希表
6. 二叉搜索树
7. 图结构
8. 并查集
9. 树状数组
10. 线段树
11. 递归树/有向无环图
12. 图遍历
13. 最小生成树
14. 单源最短路径
15. 循环查找
16. 后缀树
17. 后缀数组
18. 计算几何
19. 凸体船体
20. 网络流
21. 二分匹配
22. 最小顶点覆盖
23. Steiner Tree
24. 旅行商问题

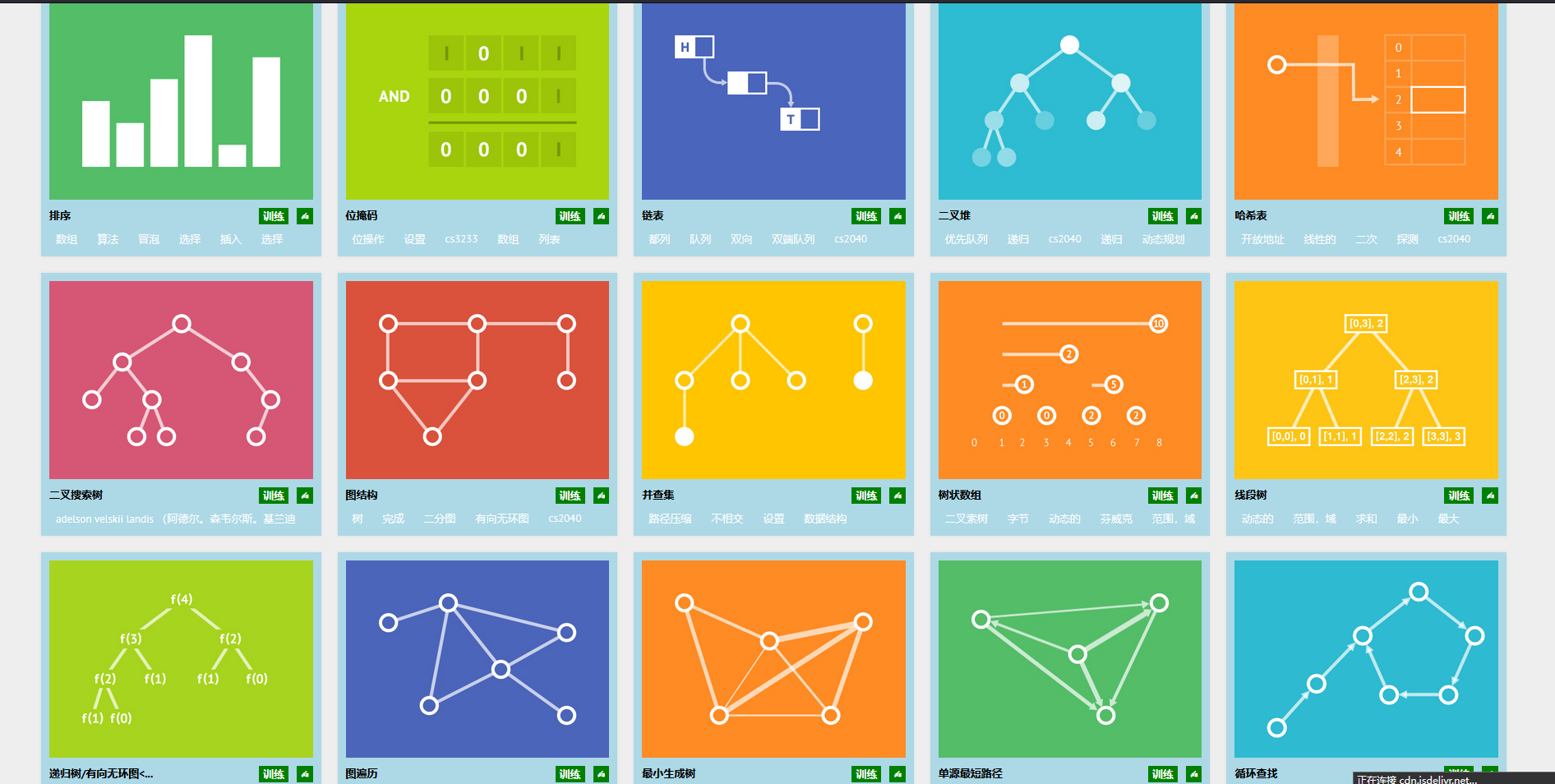
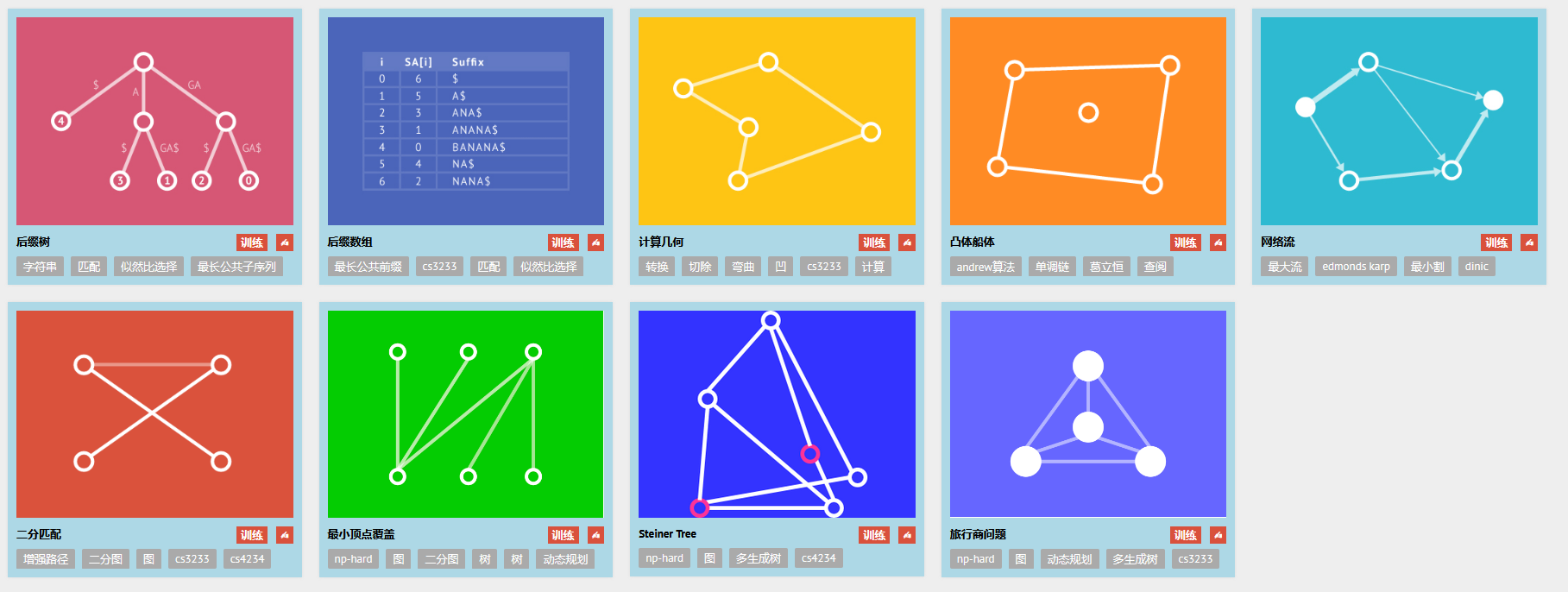
在网上看大家都是推荐visualgo，但很少有深入的文档可以学习，所以天天准备在这里详细介绍下ヾﾉ≧∀≦)o!

1. 排序

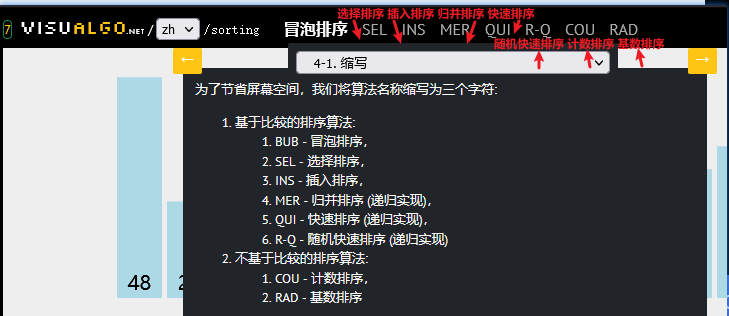
排序是计算机科学中的一种重要算法，它可以将一组数据按照某个规则进行排列。常见的排序算法有冒泡排序、插入排序、选择排序、快速排序、归并排序等。

冒泡排序

排序算法将一串数组（一个列表）中的元素（整数，数字，字符串等）按某种顺序（增大，减小，字典顺序等）重新排列。 有很多种不同的排序算法，每一种都有各自的优势和限制。 排序常常作为计算机课程中的介绍性问题，用以介绍一系列的算法思路。 不失普遍性，我们在此可视化中，只将（可能包含重复）的整数数组排序至非减。 试试点击 Bubble Sort 来可视化五个（含重复项）的杂乱整数的排序。

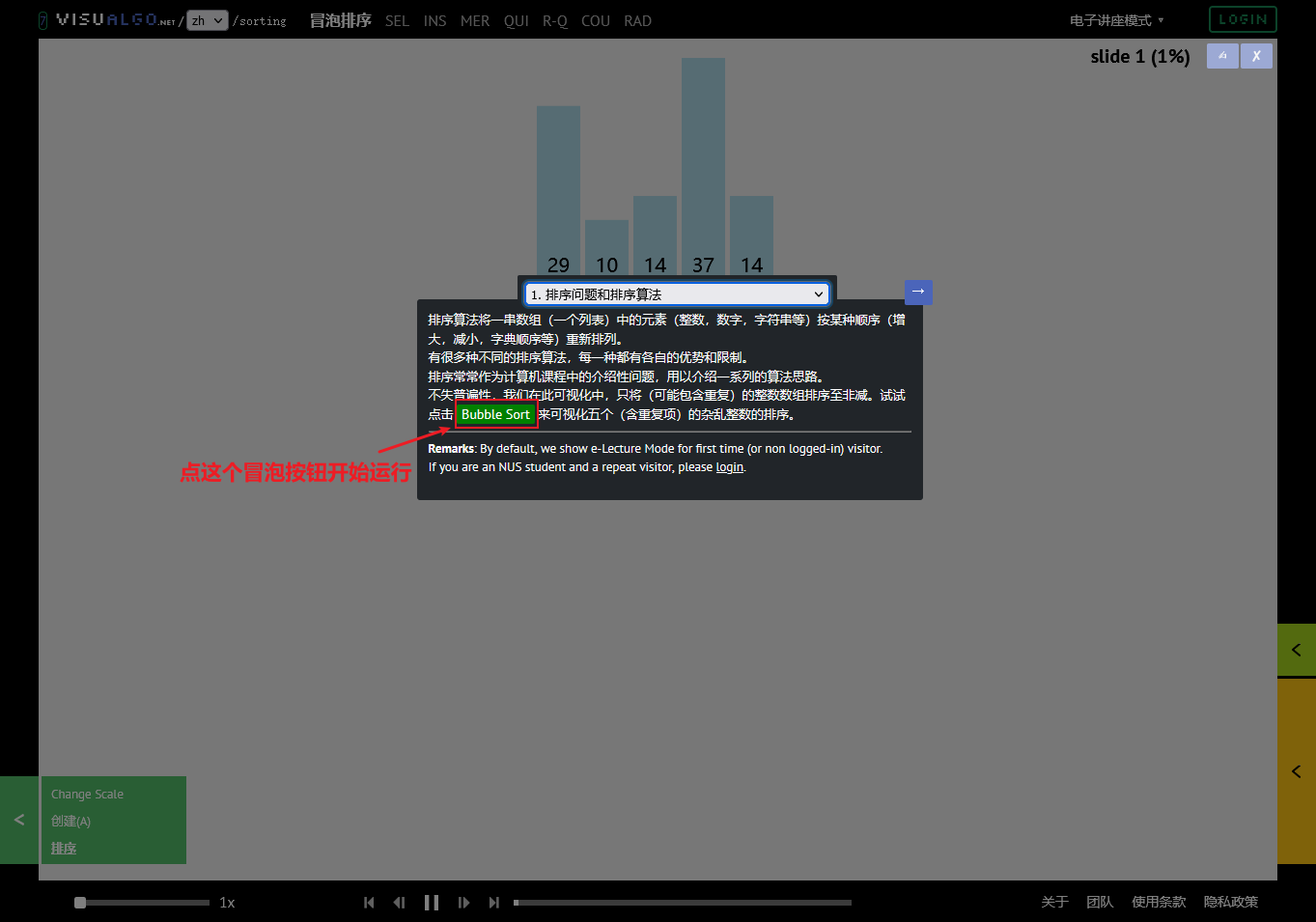
动态显示：

伪代码：

Swapped=false
从i=1到最后一个没有排序过元素的索引-1
	如果左边元素＞右边元素
		交换（左边元素，右边元素）
		Swapped=true;++swapcounter（交换计数器）
while Swapped

选择排序

动态显示：

伪代码

重复（元素个数-1）次
	把第一个没有排序过的元素设置为最小值
	遍历每个没有排序过的元素
		如果元素＜现在的最小值
			将此元素设置成为新的最小值
	将最小值和第一个没有排序过的位置交换

插入排序

动态显示：

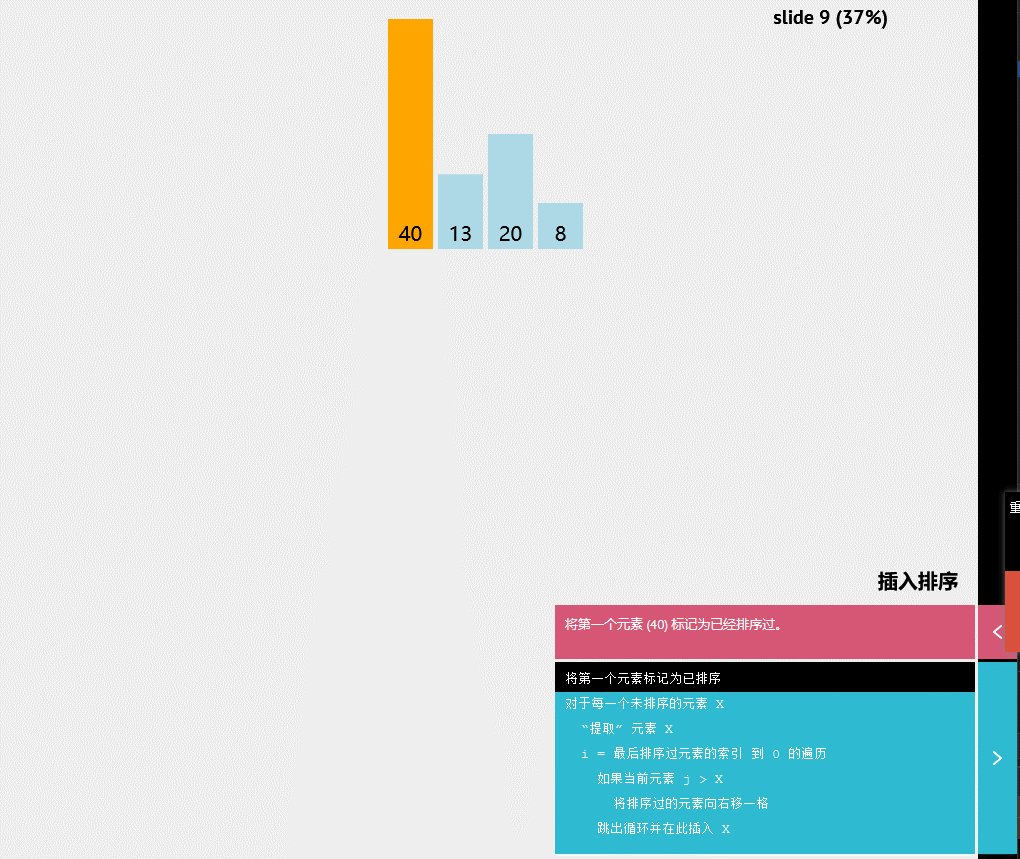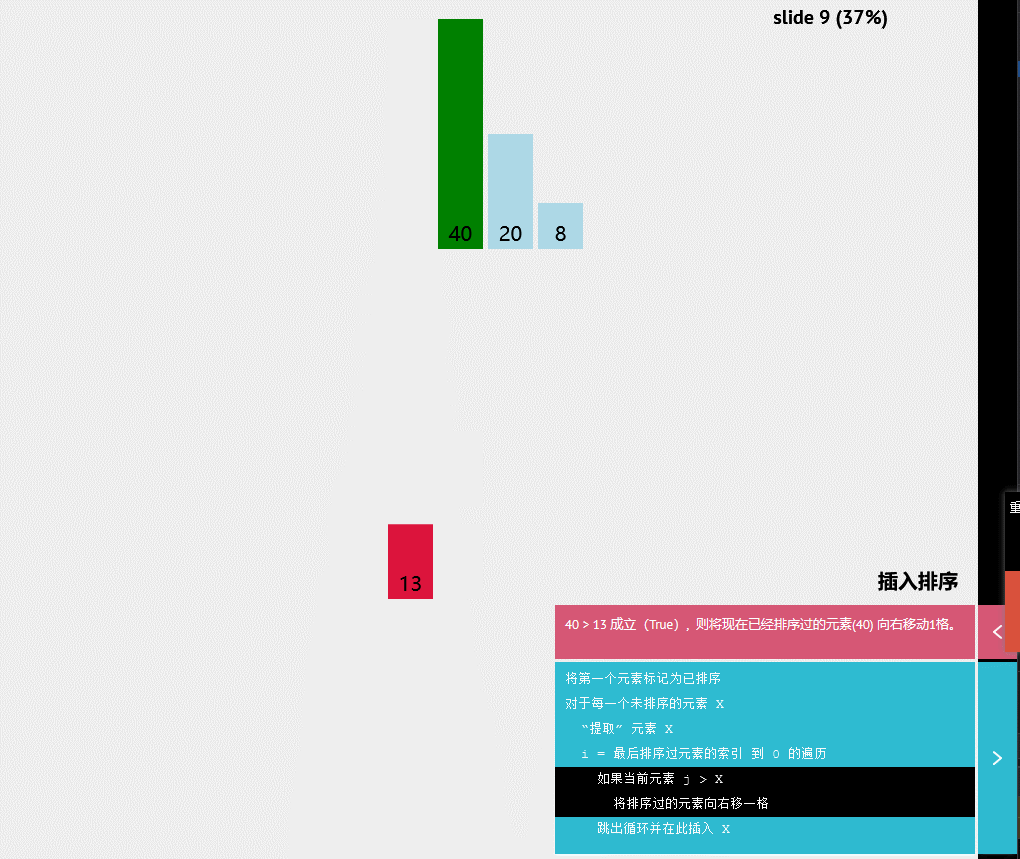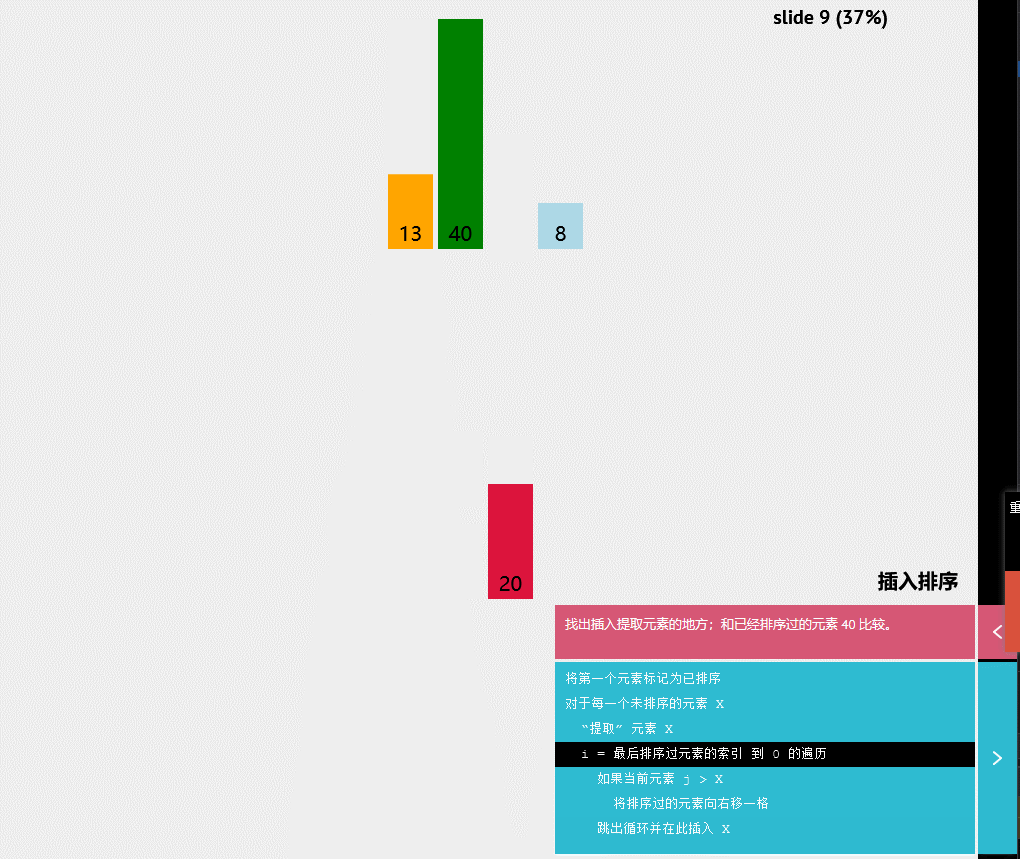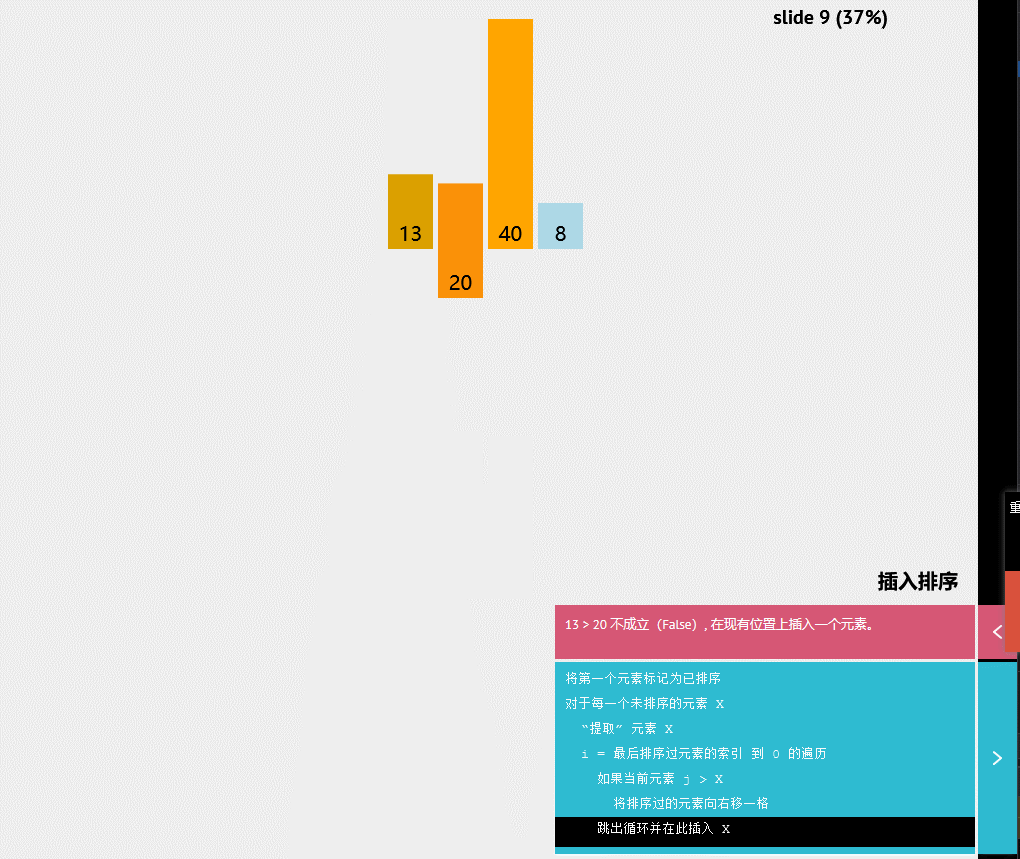
伪代码

将第一个元素标记为已排序
对于每一个未排序的元素X
	“提取”元素X
	i=最后排序过元素的索引到0的遍历
		如果当前元素j＞X
			将排序过的元素向右移一格
		跳出循环并在此插入X

归并排序

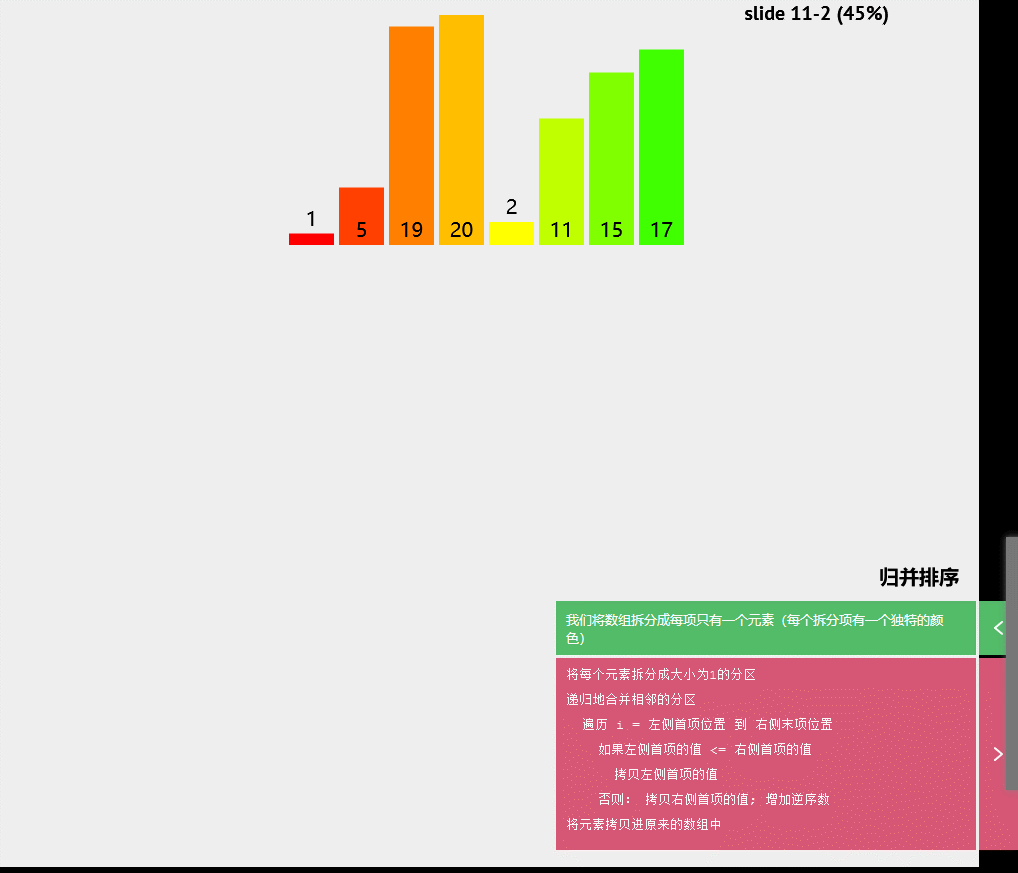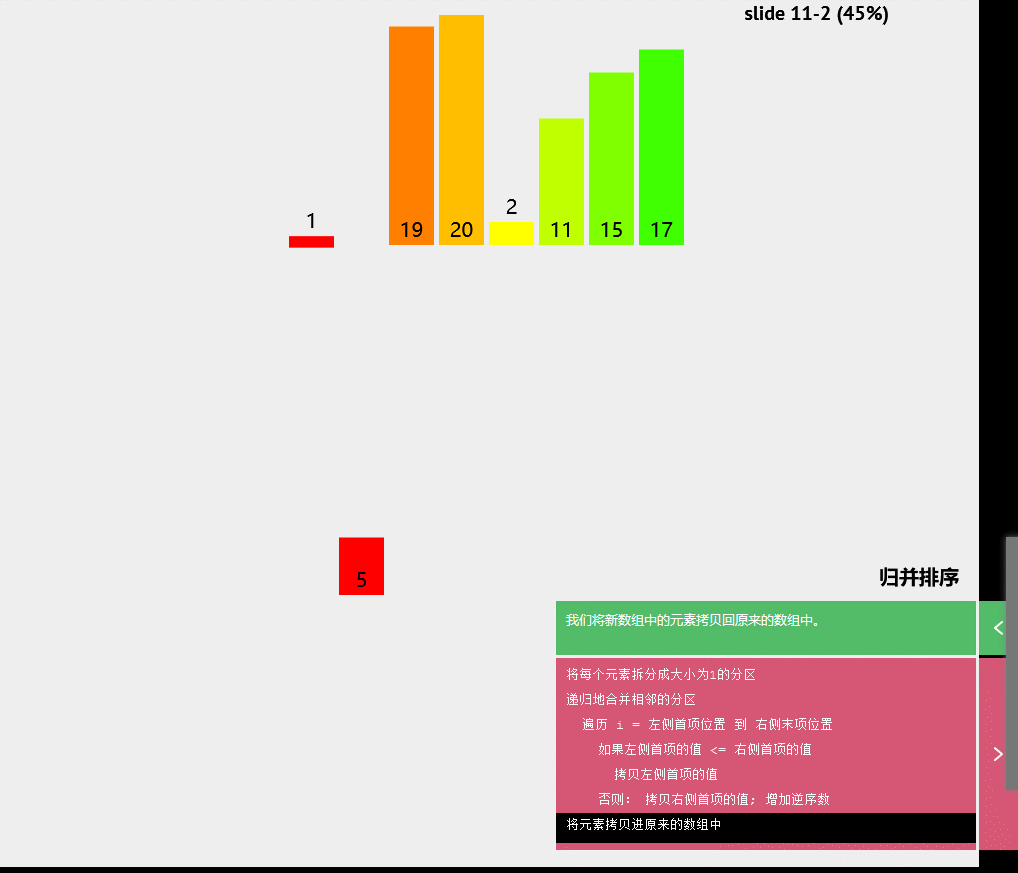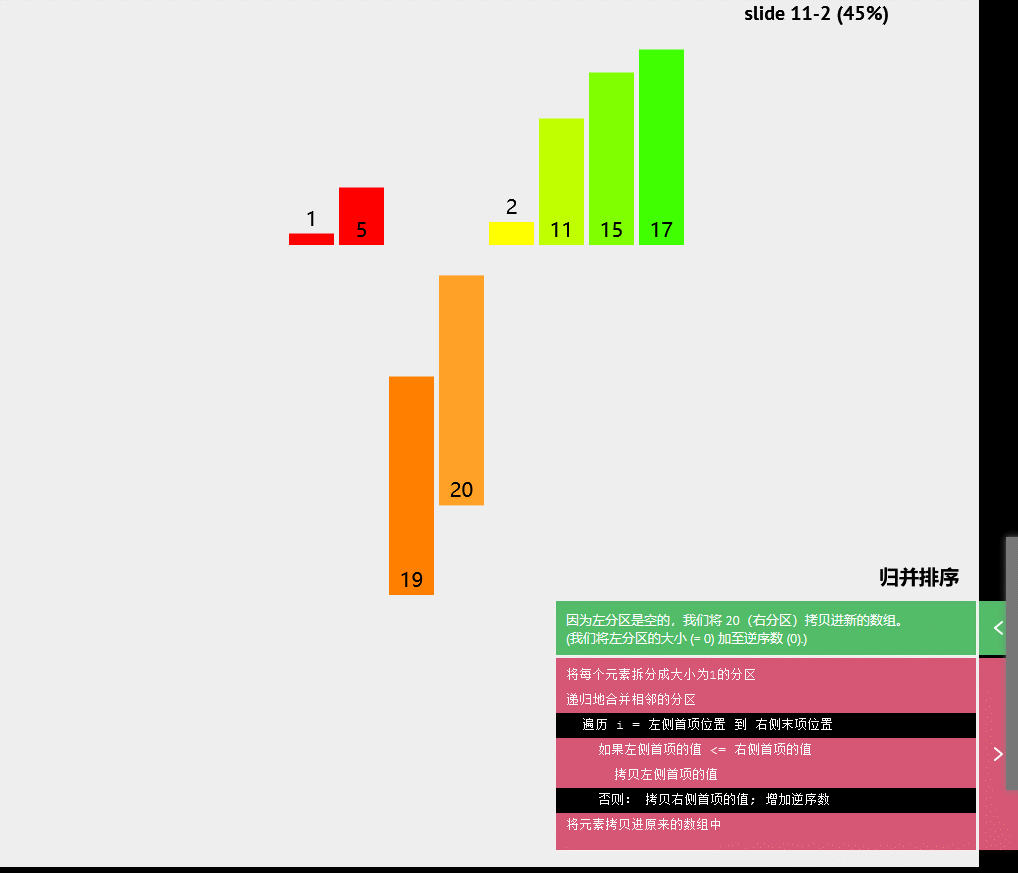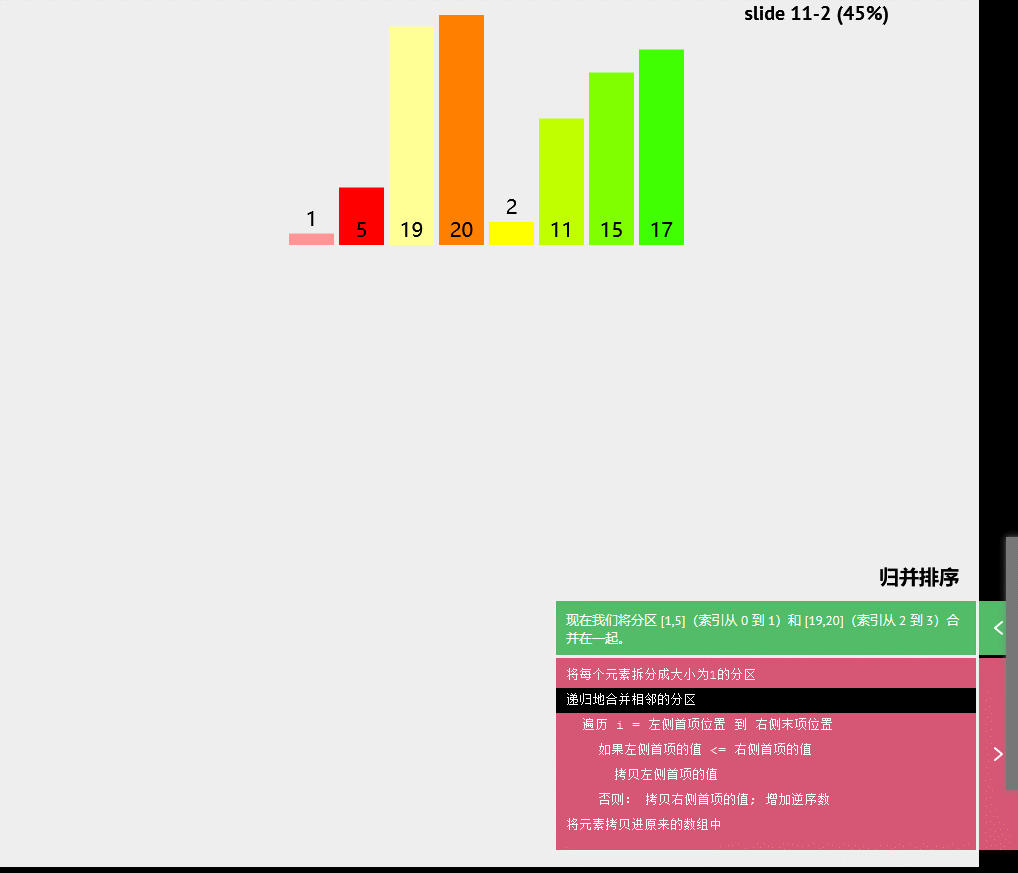
伪代码

将每个元素拆分成大小为1的分区
递归地合并相邻的分区
	遍历i=左侧首项位置到右侧末项位置
		如果左侧首项的值<=右侧首项的值
			拷贝左侧首项的值
		否则：拷贝右侧首项的值：增加逆序数
将元素拷贝进原来的数组中

快速排序

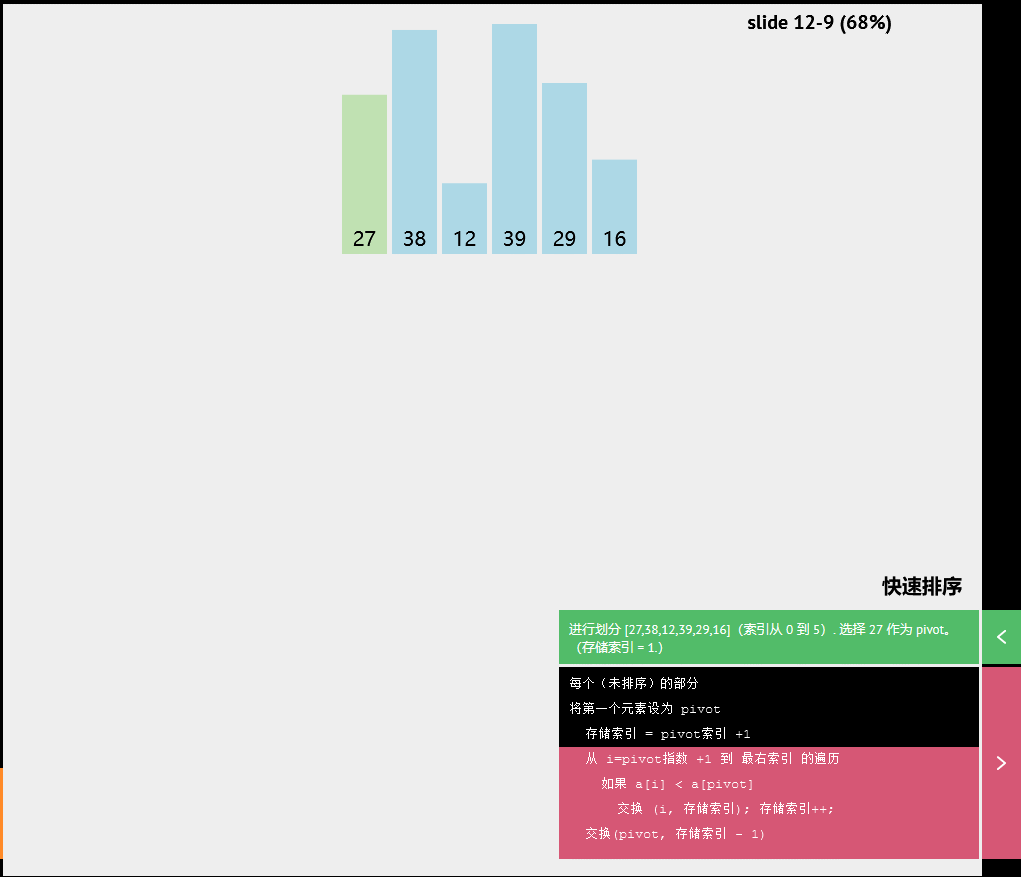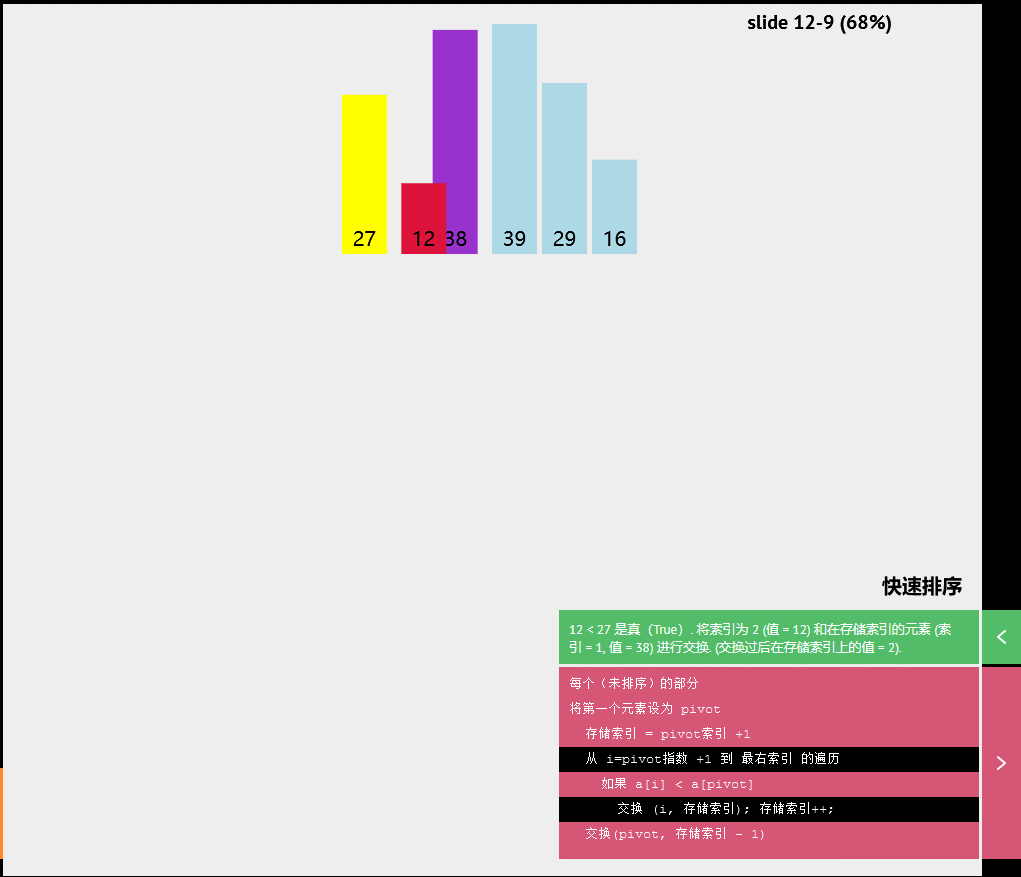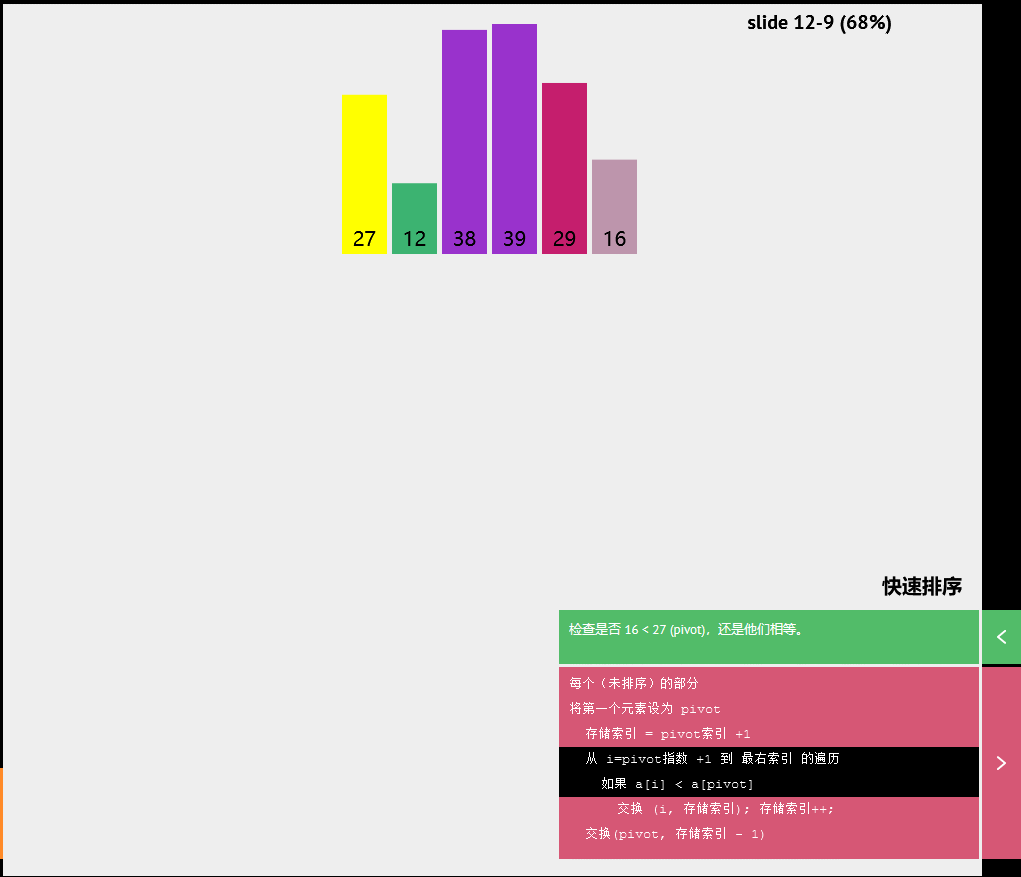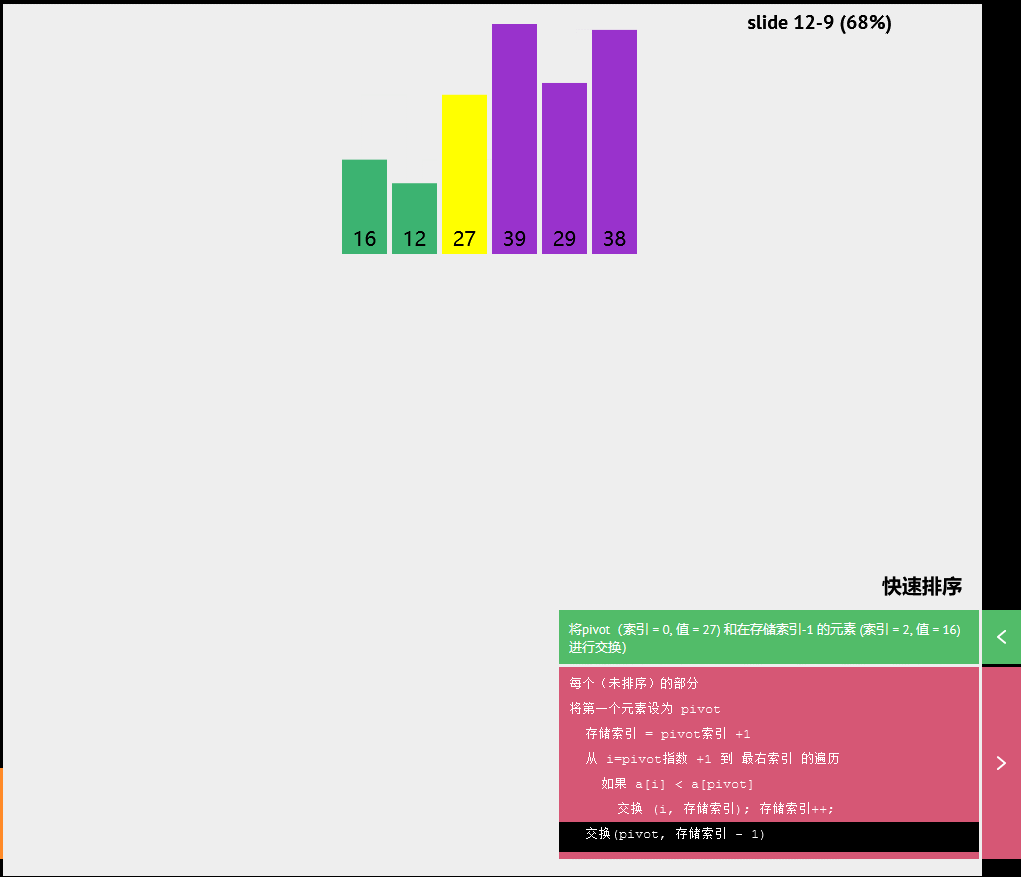
伪代码

每个（未排序）的部分
将第一个元素设为pivot
	存储索引=pivot索引+1
	从i=pivot指数+1 到 最右索引 的遍历
		如果a[1]<a[pivot]
			交换（1，存储索引）;存储索引++;
	交换（p1vot，存储索引-1）

随机快速排序

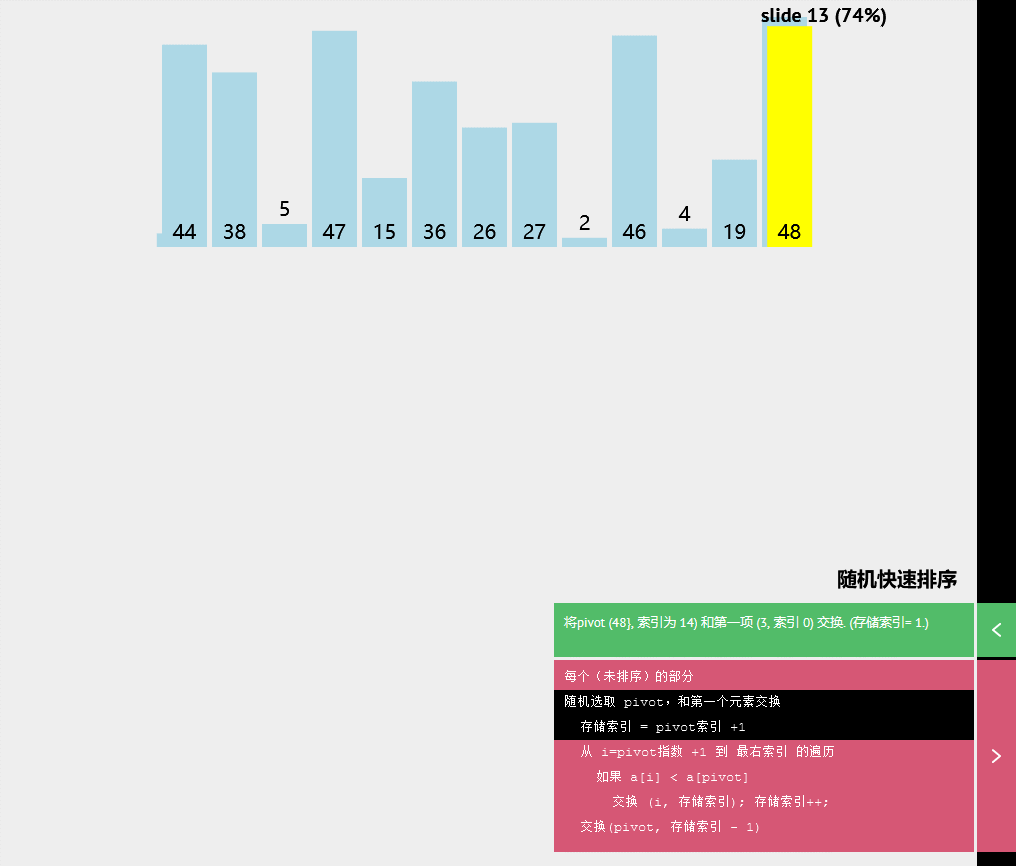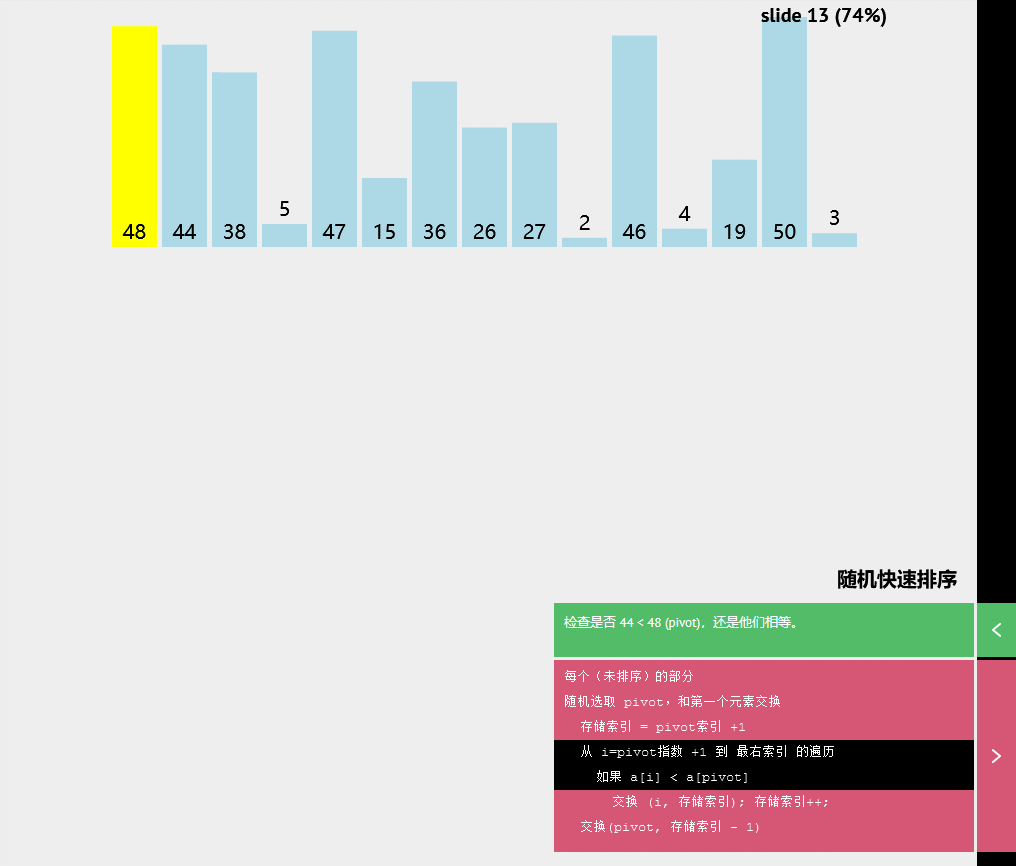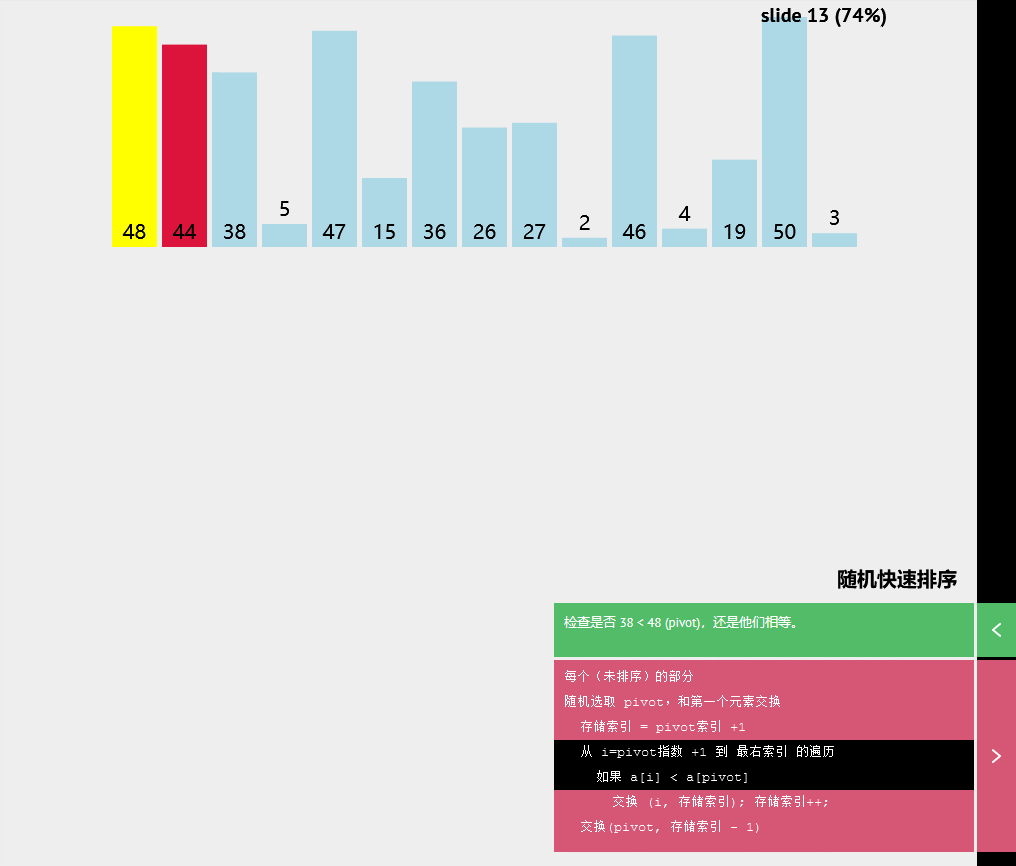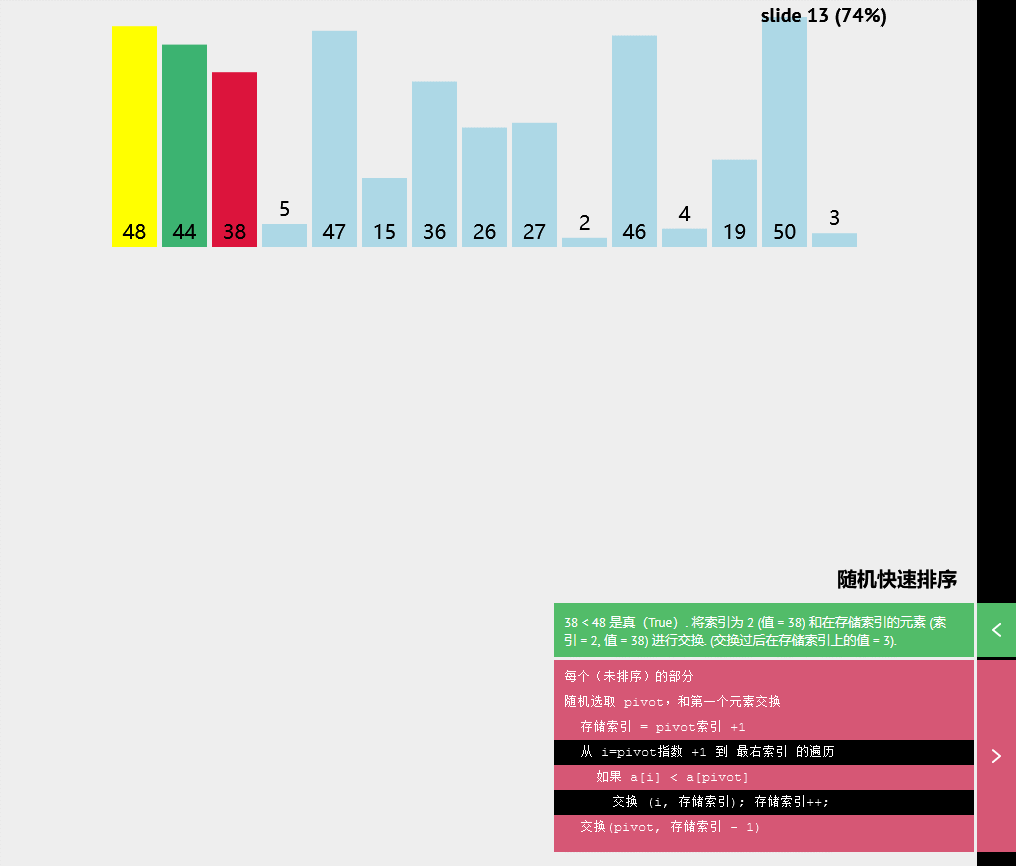
伪代码

每个（未排序）的部分
随机选取pivot，和第一个元素交换
	存储索引=pivot索引+1
	从i=pivot指数+1到最右索引的遍历
		如果a[i]<a[pivot]
			交换（i，存储索引）；存储索引++；
	交换（pivot，存储索引-1）

计数排序

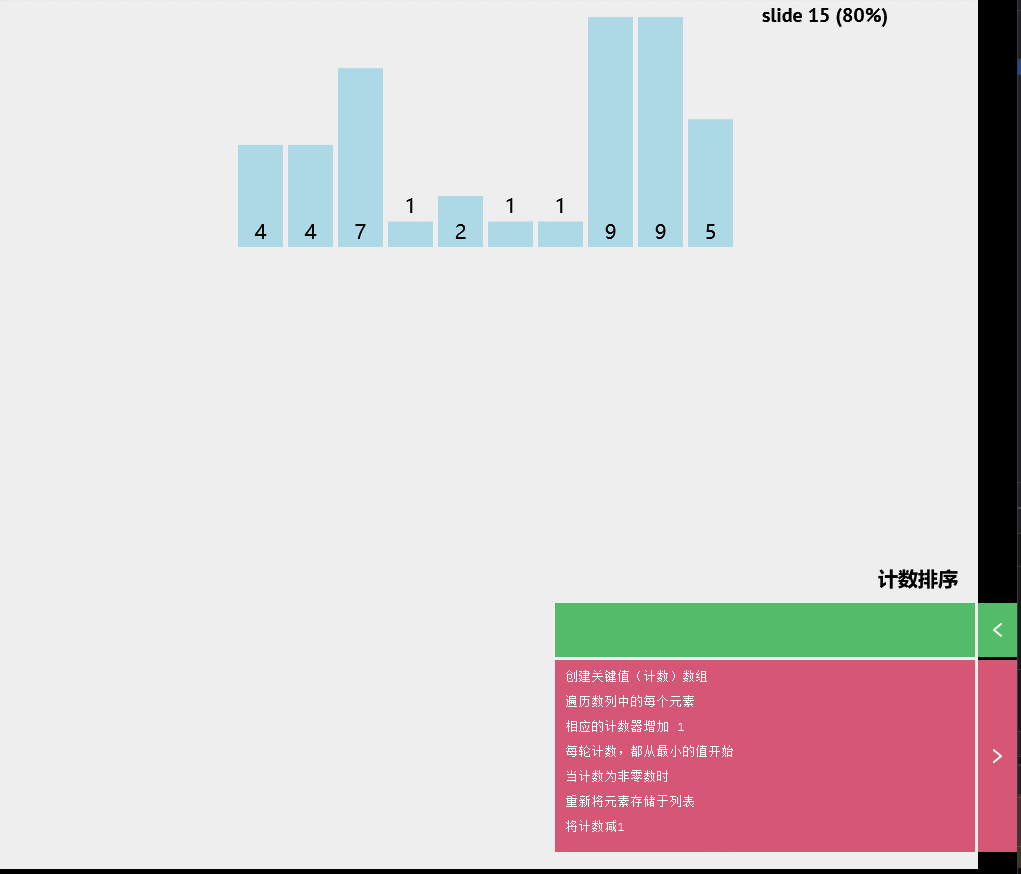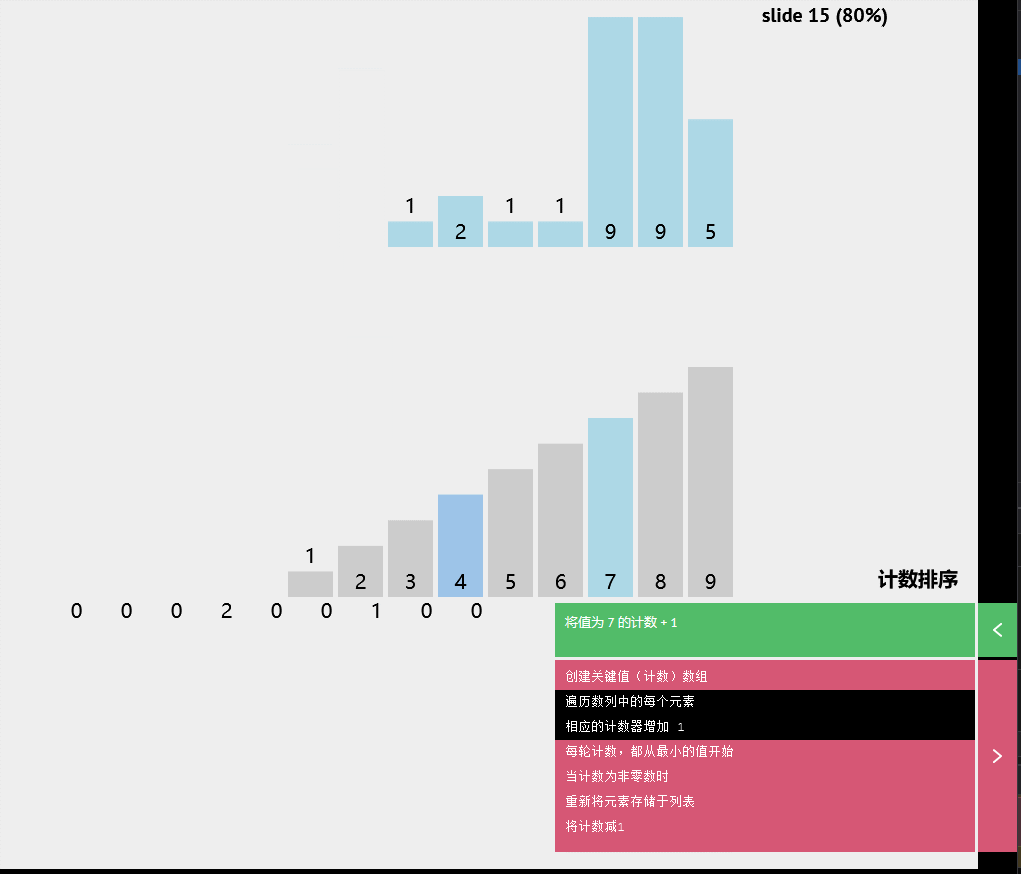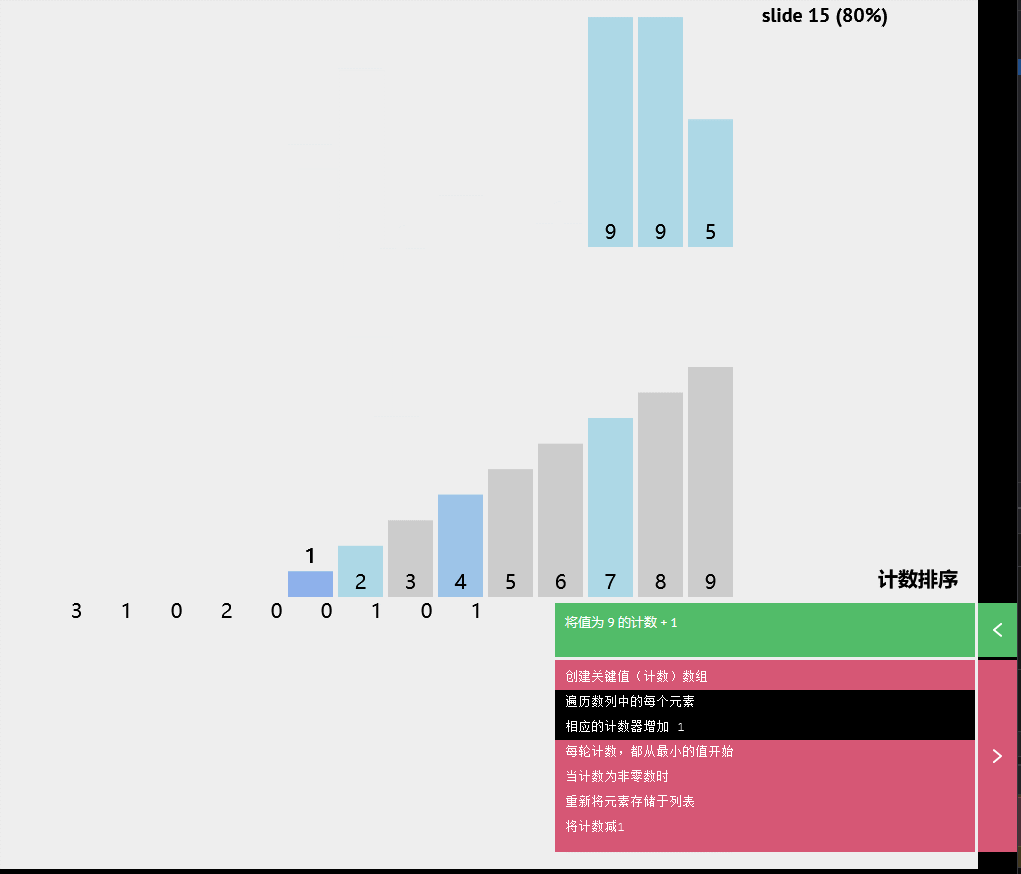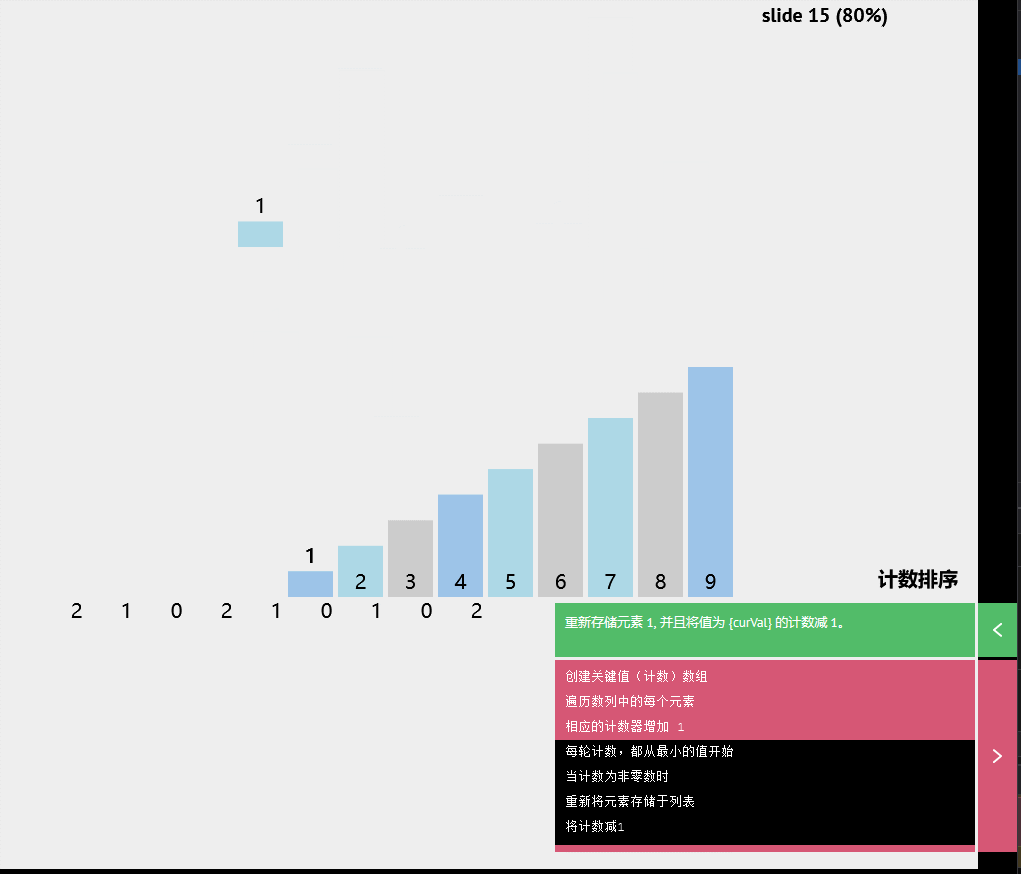
基数排序

以上是8个常见的排序算法，总结来说：

排序问题有各种有趣的算法解决方案，体现了许多计算机科学的思想:

1. 比较与非比较策略，
2. 迭代与递归实现，
3. 分而治之范式(例如，合并排序或快速排序);
4. 最佳/最差/平均情况下的时间复杂度分析
5. 随机算法等。

当（整数）数组 A 有序时，涉及 A 的许多问题变得简单（至少比原本简单）：

• 在数组 A 中搜索特定值 v，
• 查找（静态）数组 A 中的最小/最大/第 k 个最小/最大值，
• 测试唯一性并删除数组 A 中的重复项，
• 计算特定值 v 在数组 A 中出现多少次，
• 设置数组 A 和另一个排序数组 B 之间的交集/联合，
• 寻找一个目标对 x∈A 和 y∈A，使得 x + y 等于目标 z 等。
• 计算在区间 [lo…hi] 内共计有多少个值。

2. 位掩码

位掩码也称为掩码运算，是计算机科学中的一种基本操作。通过与位掩码进行按位与、或、异或等运算，可以实现对二进制数位的精确控制，常用于编码、加密和解密等场景。

3. 链表

链表是一种基本的线性数据结构，它由节点组成，每个节点包含一个值和指向下一个节点的指针。相比于数组，链表不需要连续的内存空间，并且可以随意插入和删除节点，因此在某些场景下更加灵活。

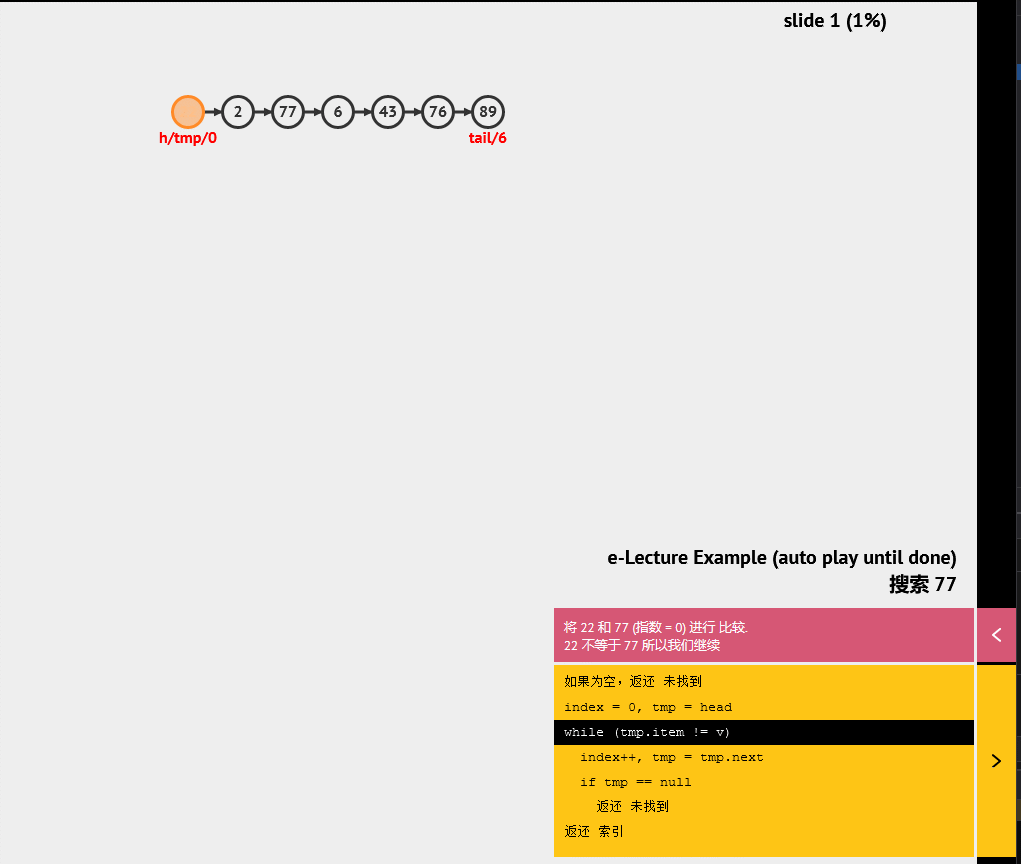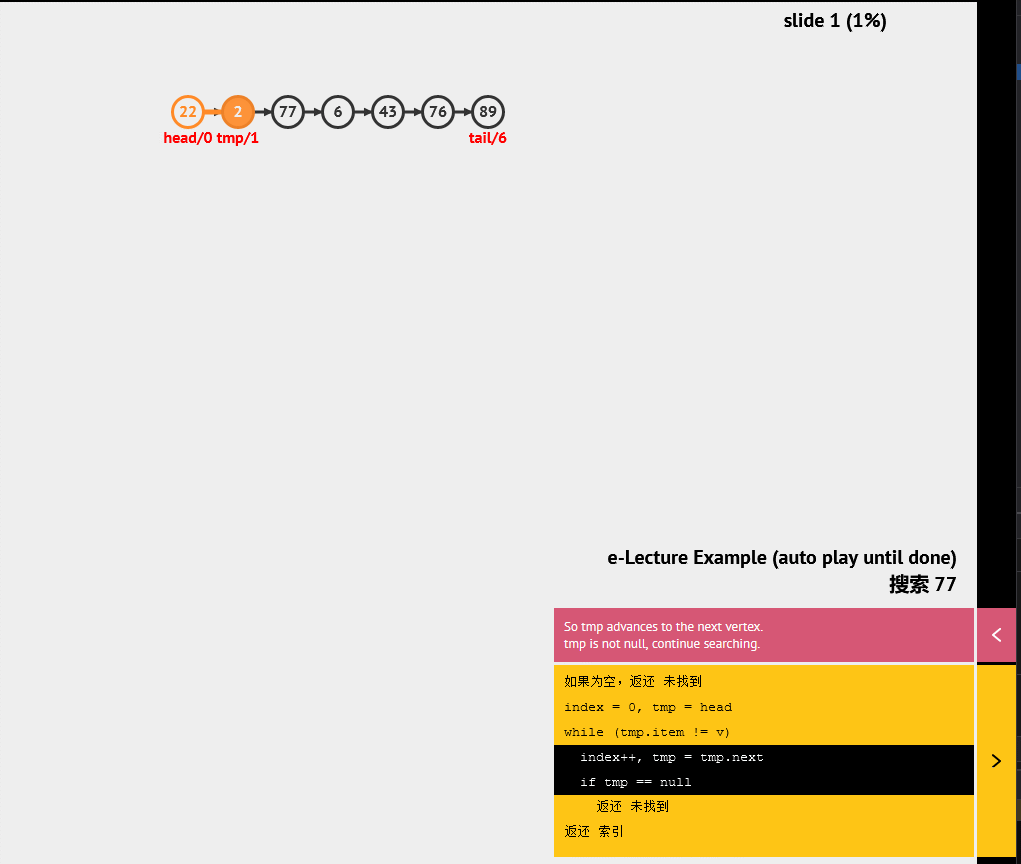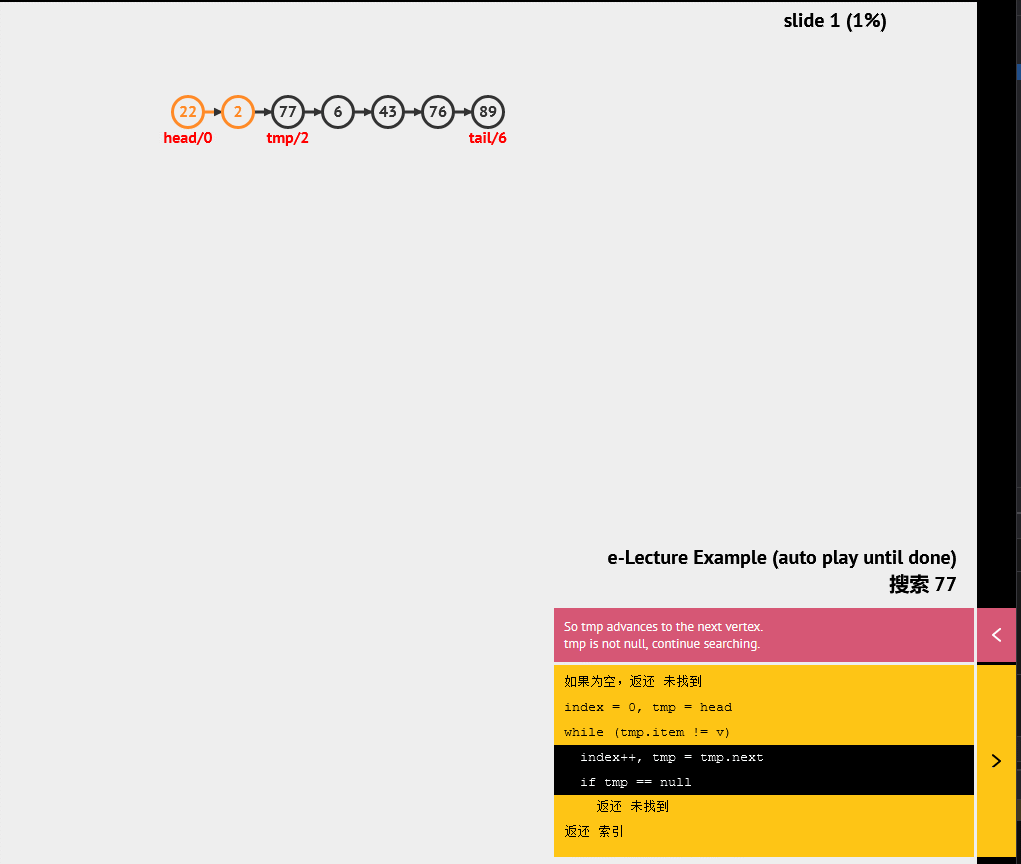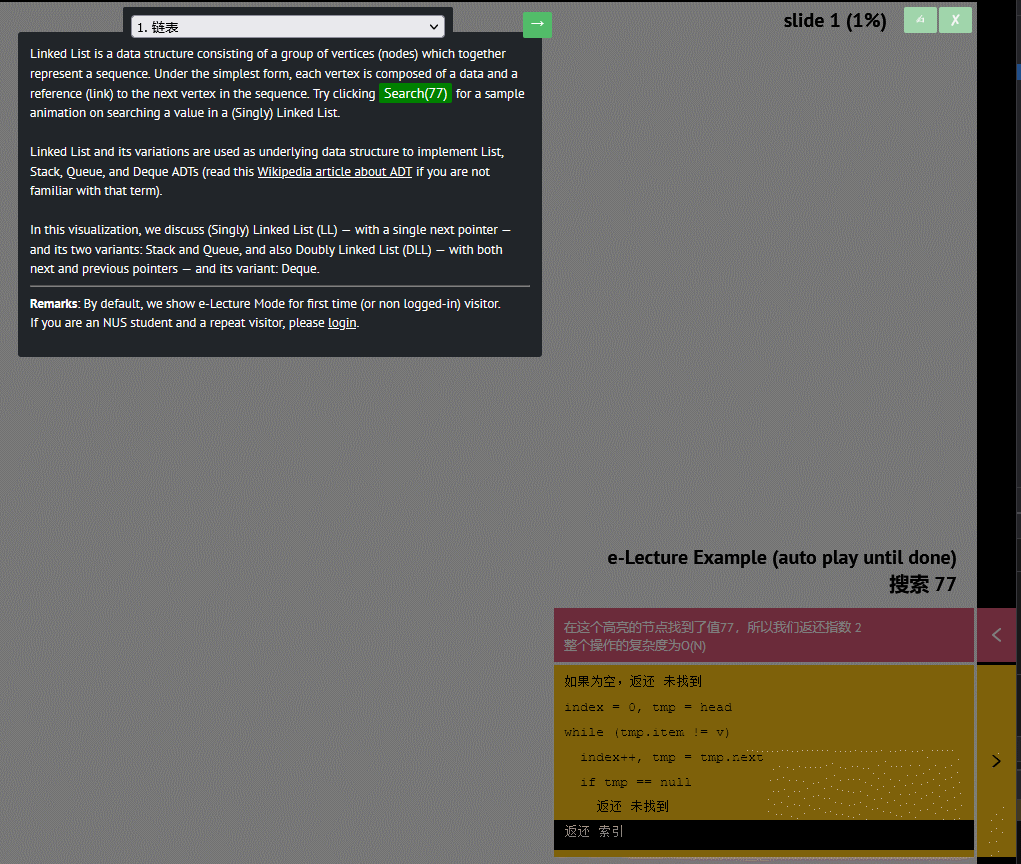
4. 二叉堆

二叉堆是一种基于完全二叉树的数据结构，可以用来实现优先队列。二叉堆分为最大堆和最小堆两种形式，在最大堆中，每个节点的值都大于其子节点的值；在最小堆中，每个节点的值都小于其子节点的值。

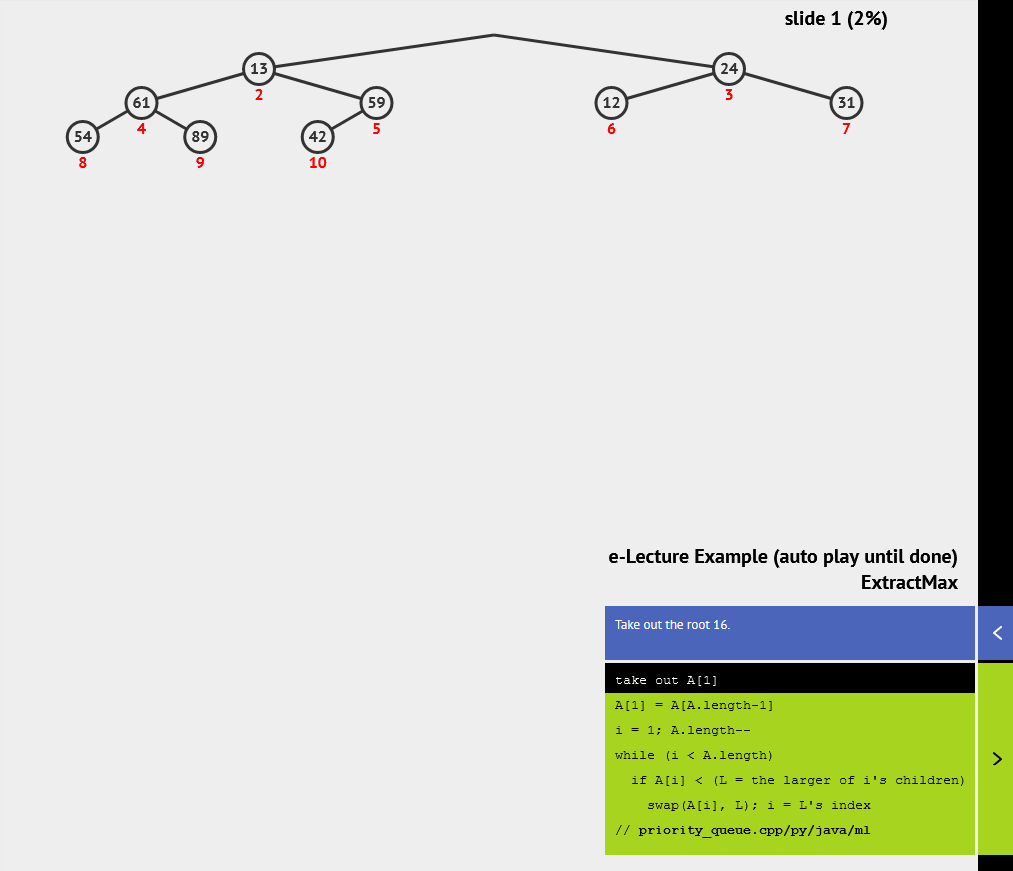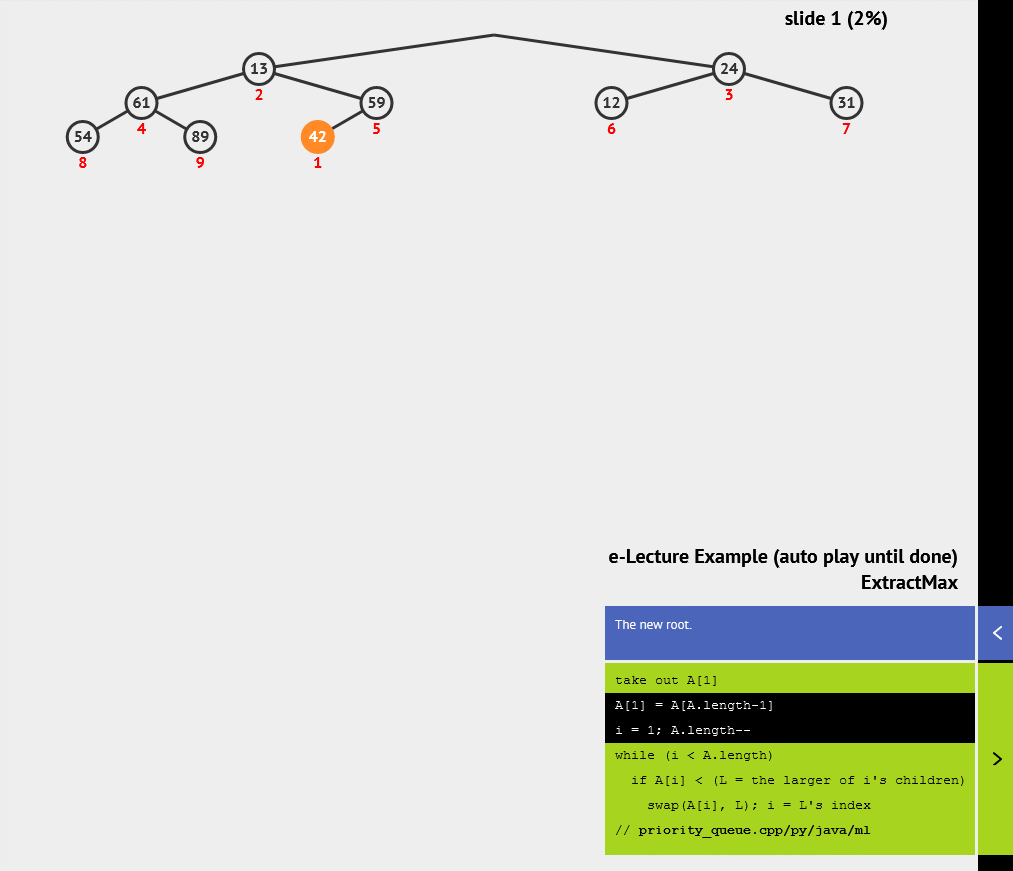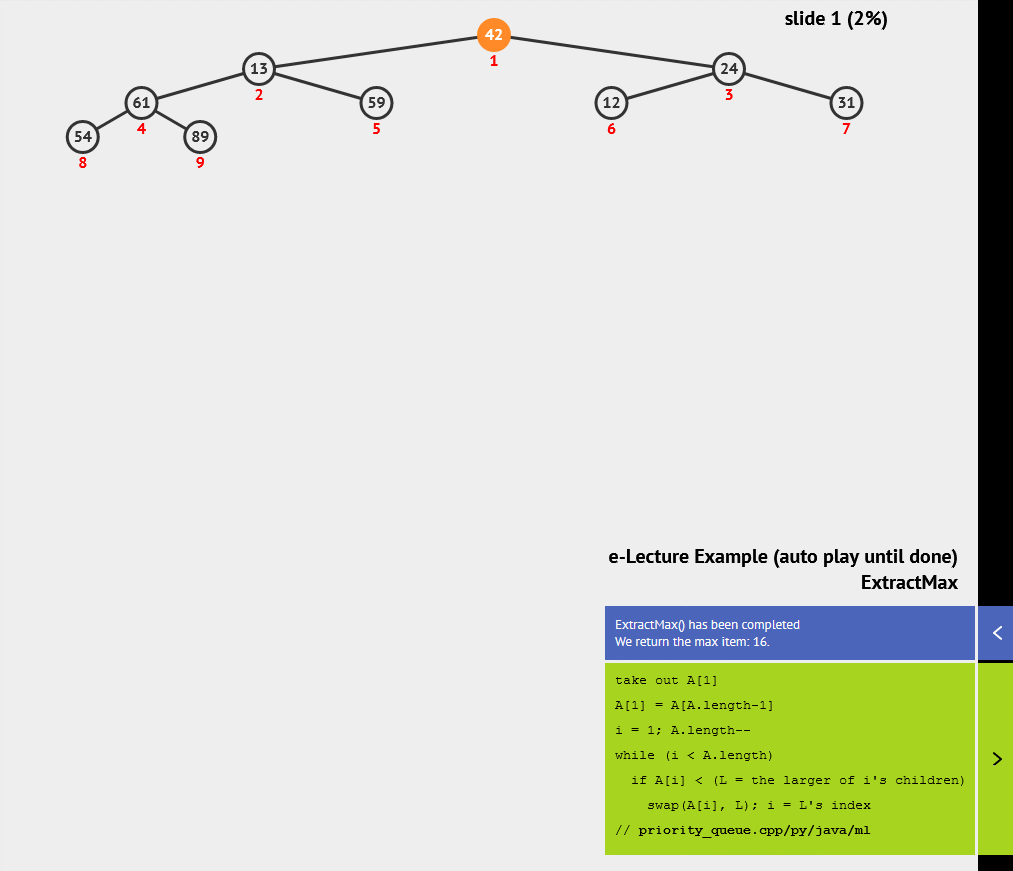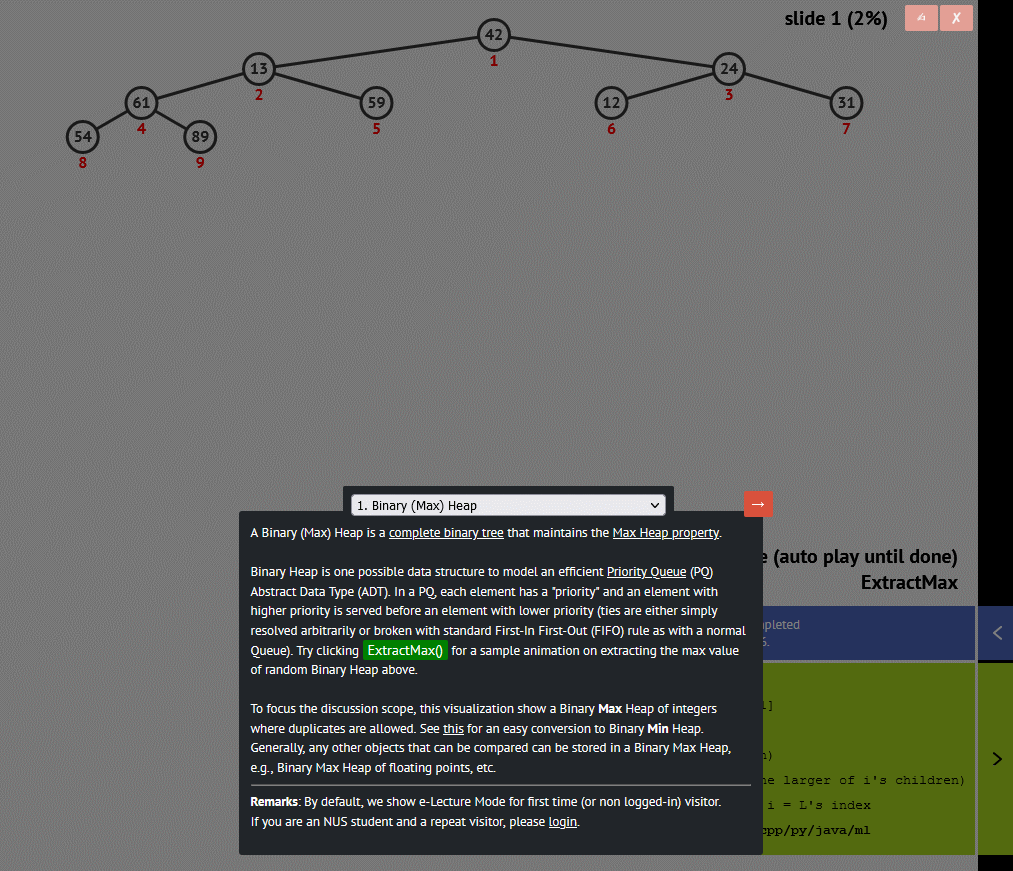
5. 哈希表

哈希表也称为散列表，是一种以键-值对形式存储数据的数据结构。哈希表通过将键映射到数组下标来实现快速查找和插入，其时间复杂度通常为O(1)。

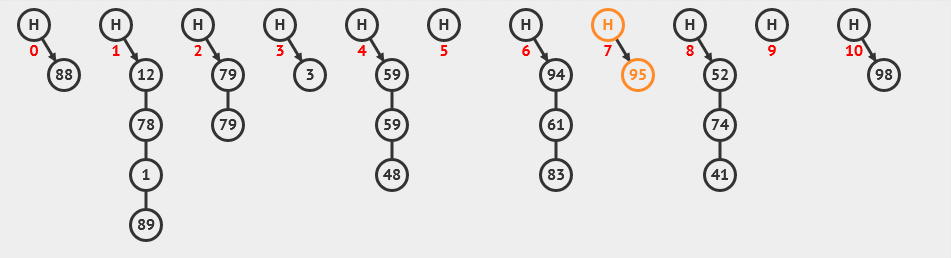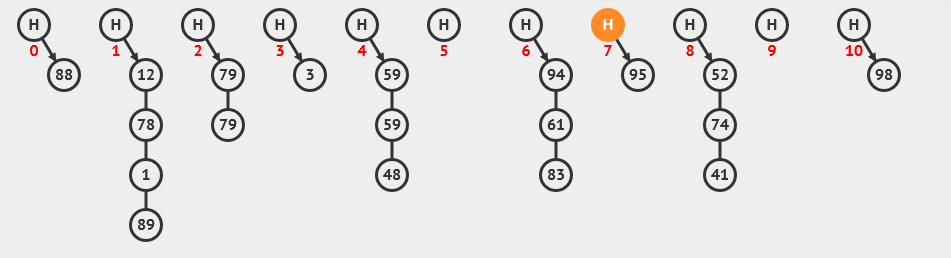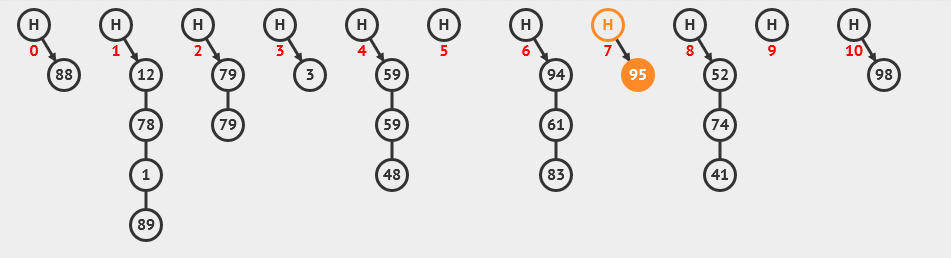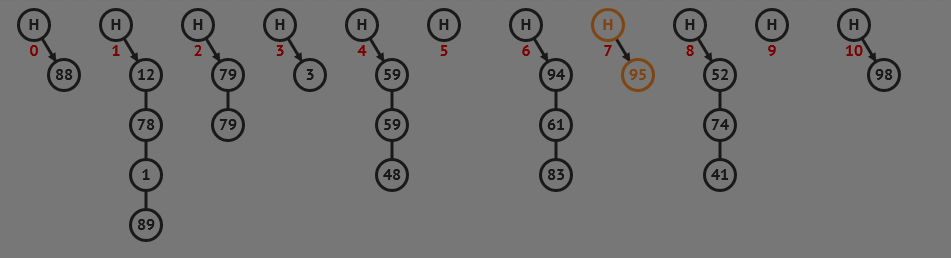
6. 二叉搜索树

二叉搜索树是一种基于二分查找思想的数据结构，它具有良好的查找和插入性能。在一个二叉搜索树中，每个节点都比其左子树的所有节点大，比其右子树的所有节点小。

7. 图结构

图是一种非线性的数据结构，由节点和边组成。图可以用来表示网络、关系等概念，并且在许多领域中都得到了广泛应用。

8. 并查集

并查集是一种用于处理不相交集合的数据结构。它支持合并两个集合和查询两个元素是否在同一个集合中，常用于解决连通性问题。

9. 树状数组

树状数组是一种用于维护前缀和的数据结构，支持单点修改和区间查询操作。它可以在O(log n)的时间内完成这些操作，比暴力算法更加高效。

10. 线段树

线段树是一种用于维护区间和的数据结构，支持区间修改和区间查询操作。它可以在O(log n)的时间内完成这些操作，比暴力算法更加高效。

11. 递归树/有向无环图

递归树和有向无环图是用于分析递归算法复杂度的工具。递归树将递归算法转化为树形结构进行分析，而有向无环图则可以用来处理递推式的复杂度。

12. 图遍历

图遍历是指按照一定规则访问图中所有节点的过程。常见的图遍历算法有深度优先搜索（DFS）和广度优先搜索（BFS）。

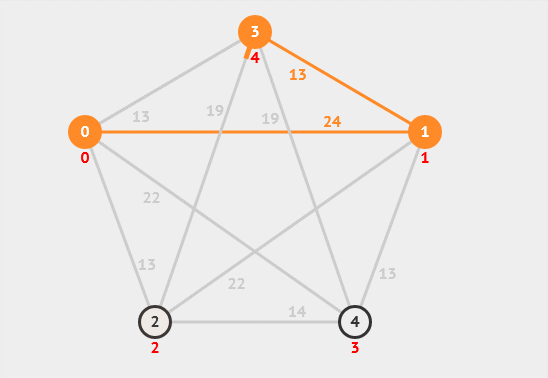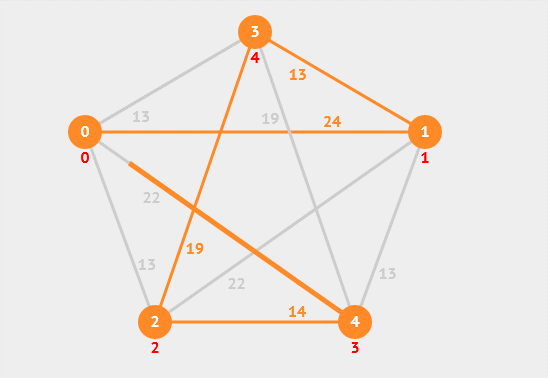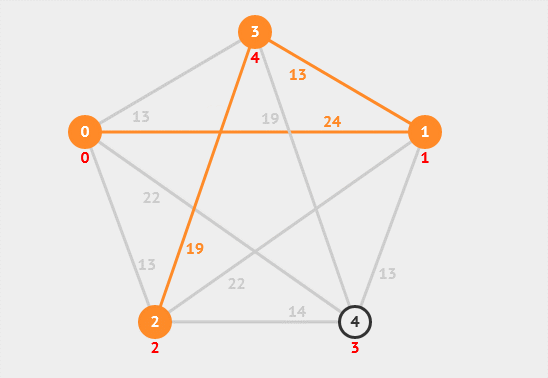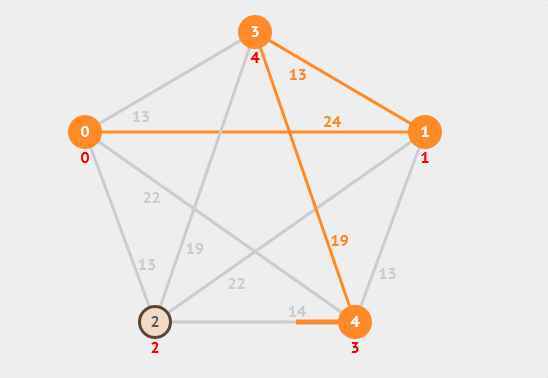
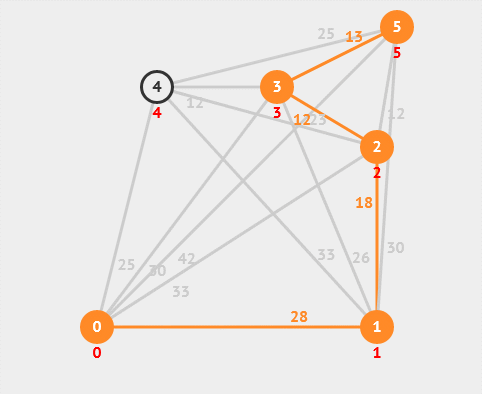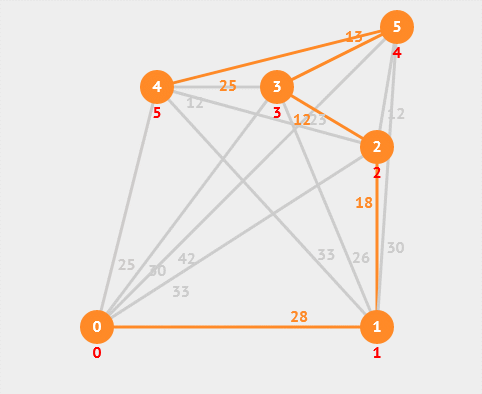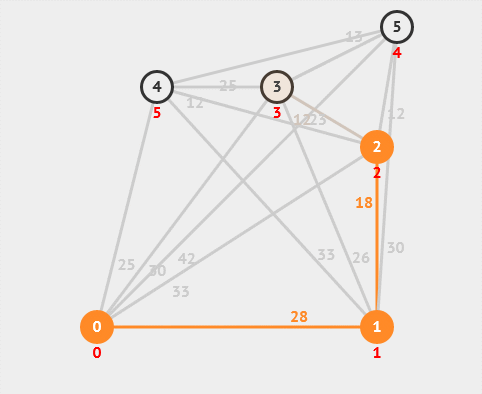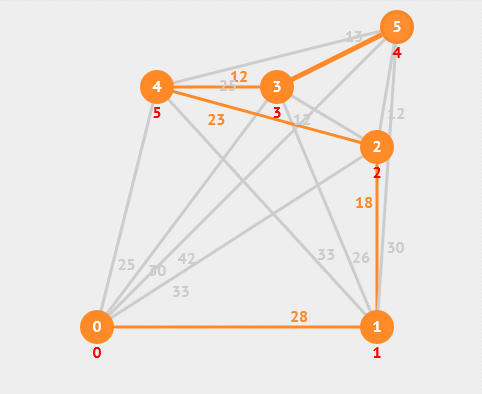
13. 最小生成树

最小生成树是指在一个加权连通图中，找到一棵包含所有节点且边权值之和最小的生成树。常用的最小生成树算法有Prim算法和Kruskal算法等。

14. 单源最短路径

单源最短路径是指从一个起点到所有其他节点的最短路径。常用的单源最短路径算法有Dijkstra算法和Bellman-Ford算法等。

15. 循环查找

循环查找也称为哈希冲突解决方法，用于处理哈希表中键的冲突。常见的循环查找方法有线性探测、二次探测和双重散列等。

16. 后缀树

后缀树是一种特殊的字符串数据结构，可以用来高效地处理字符串匹配问题。它可以在O(m)的时间内完成字符串匹配操作，其中m为模式串的长度。

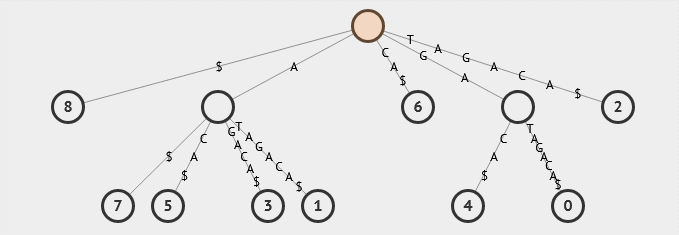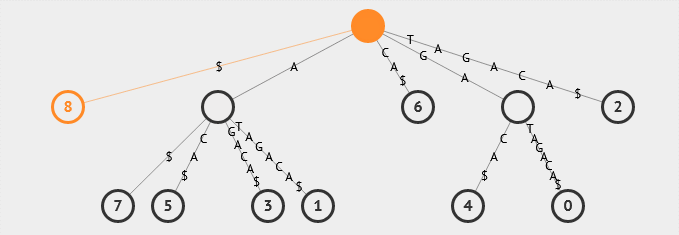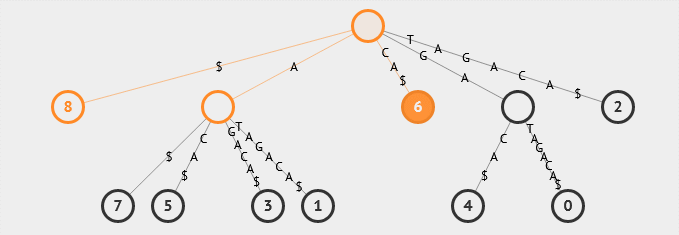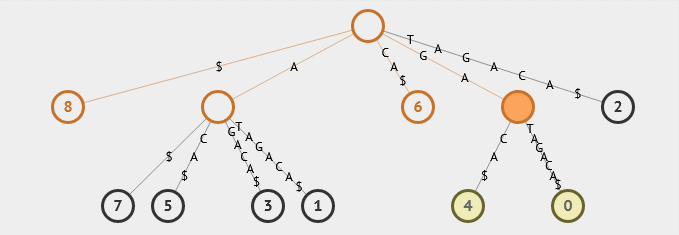
17. 后缀数组

后缀数组是一种用于处理字符串排序和匹配的数据结构。它可以在O(n log n)的时间内完成排序操作，比后缀树更加高效。

18. 计算几何

计算几何是一种研究空间中的几何形体和其性质的学科。在算法竞赛中，计算几何常用于解决求凸包、最近点对等问题。

周长计算

面积计算

19. 凸体船体

凸体船体是指在一个二维平面上，由一组点构成的最小凸多边形。该问题可以用于处理机器人路径规划等应用场景。

20. 网络流

网络流是一种图论算法，用于建模和解决最大流/最小割问题。其中最大流表示从源点到汇点的最大流量，最小割表示将图分为两个不相交的部分的最小代价。

21. 二分匹配

二分匹配是一种用于解决二分图匹配问题的算法。它可以在O(m√n)的时间内完成匹配操作，其中m为边数，n为节点数。

22. 最小顶点覆盖

最小顶点覆盖是指在一个无向图中，找到一个包含所有边所连接节点的最小节点集合。该问题可以用于处理任务调度等应用场景。

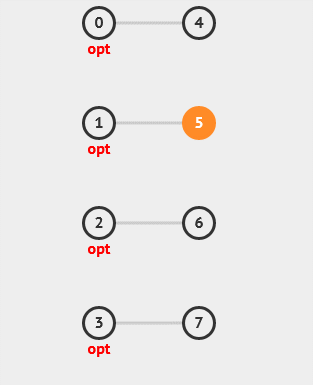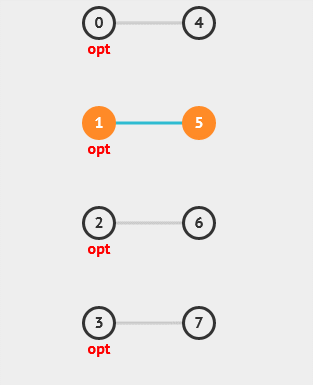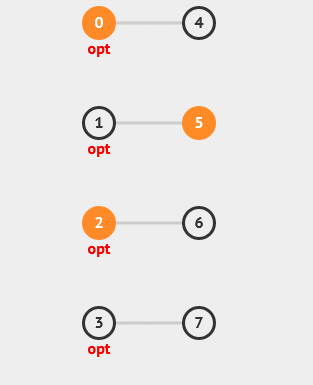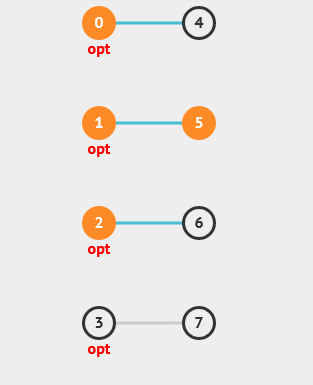
23. Steiner Tree

Steiner Tree是指在一个无向图中，找到一个包含所有指定节点的最小子图。该问题可以用于处理网络优化等应用场景。

24. 旅行商问题

旅行商问题是指在一个完全图中，找到一条经过所有节点且路径长度最短的回路。该问题可以用于处理物流配送、电路设计等应用场景。