人工智能常见知识点⑥

一．实验目的：

1. 通过实例开发，熟悉遗传搜索算法。

2. 掌握遗传搜索算法的应用

二．实验设备：

电脑

相应的开发软件Idea

三．实验要求：

问题描述

求下述二元函数的最大值：

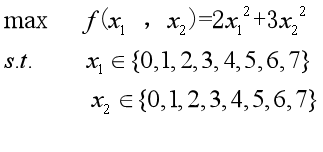
x1, x2 为 0 ~ 7之间的整数，所以分别用4位无符号二进制整数来表示，将它们连接在一起所组成的8位无符号二进制数就形成了个体的基因型，表示一个可行解。

个体的表现型x和基因型X之间可通过编码和解码程序相互转换。

（1）设计遗传搜索算法；

（2）实现遗传搜索算法求解二元函数的最大值；

（3）比较遗传搜索算法和其他搜索算法应用的优缺点。

四．实验步骤：

1． 程序设计

程序流程图如下：

适应度函数说明如下：

这个适应度函数返回的一个是一个每一个群体及其对应的适应度的键值对，以便后续进行选择算法的时候根据适应度大小进行选择。

初始种群选择说明：

根据x1,x2的范围进行随机生成四个数值对(x1,x2)。

选择算法说明：

首先如果是第一次循环则需要执行初始种群的函数，然后进行适应度进行计算得出每个种群的适应度占比，然后根据适应度占比来进行选择，这里我是根据2,1,1分配来进行选择，适应度占比最大的选择2次，最小的不选择，其余选择1次。即优胜略汰，因为如果我发现是随机选择的话，执行遗传次数过多，很难得出最大适应度。所以就按照2，1，1分配，但是我发现即使是这样有时候还是难以避免遗传次数过多。

选择完成之后进行数值对及其对应的二进制重置

交叉算法说明：

首先随机生成两个数，分别代表个体编号，然后随机生成两个交叉点。两个个体编号选择其他一个交叉点进行交叉运算，即交叉点及其后面的二进制数字进行互换，再找出剩下的两个个体编号按照上述方法进行运算。

然后进行数值对及其对应的二进制重置。

变异算法说明：

随机生成四个变异点，然后个体编号根据对应的变异点对他们的二进制对应的位数进行取反。

然后进行数值对及其对应的二进制重置。

2． *****实现

附上代码如下：（用java语言进行实现）

import java.util.*;
/**
 * 遗传算法的实现
 * f(x) = 2*x1*x1 + 3*x2*x2
 */
public class ch4 {
 // 两个参数
 private static int x1, x2;
 // 参数范围
 private static int[] fangWei = {0, 1, 2, 3, 4, 5, 6, 7};
 // 初始群体
 private static int[][] xx = new int[4][2];
 // 二进制显示初始群体
 public static String[] str = new String[4];
 // 适应度占比
 public static Map<Integer,Double> x_DaXiao = new HashMap<>();
 // 群体的选择次数
 private static Map<Integer, Integer> x_times = new LinkedHashMap<>();
 // 经历代数
 public static int sum = 1;
 // 最大解
 public static int result = 0;
 // 初始群体选择算法
 public static int[][] startX() {
 System.out.println("随机初始化群体：");
 for (int i = 0; i < 4; i++) {
 xx[i][0] = (int) (Math.random() * fangWei[fangWei.length - 1]);
 xx[i][1] = (int) (Math.random() * fangWei[fangWei.length - 1]);
 }
 printXX();
 // 初始化二进制数组
 str = toBinStr(xx);
 return xx;
 }
 // 计算适应度函数
 public static Map<Integer, Integer> countShiYingDu(int[][] xx) {
 // 适应度集合
 List<Integer> flags = new ArrayList<>();
 // 适应度map
 Map<Integer, Integer> listFlag = new HashMap<>();
 int sum = 0;
 // 计算适应度
 for (int i = 0; i < 4; i++) {
 int num = 2 * xx[i][0] * xx[i][0] + 3 * xx[i][1] * xx[i][1];
 flags.add(num);
 listFlag.put(i, num);
 sum += num;
 }
 // 计算百分比
 for (int j = 0; j < 4; j++) {
 double DaXiao = flags.get(j) / (double) sum;
 String str = String.format("%.2f", DaXiao);
 DaXiao = Double.parseDouble(str);
 x_DaXiao.put(j, DaXiao);
 }
 flags.sort(Comparator.naturalOrder());
 // 最大的适应度
 result = flags.get(3);
 return listFlag;
 }
 public static void selectXX(Map<Integer, Integer> listFlag) {
 int times = 0;
 //利用Map的entrySet方法，转化为list进行排序
 List<Map.Entry<Integer, Integer>> entryList = new ArrayList<>(listFlag.entrySet());
 //利用Collections的sort方法对list排序
 Collections.sort(entryList, new Comparator<Map.Entry<Integer, Integer>>() {
 @Override
 public int compare(Map.Entry<Integer, Integer> o1, Map.Entry<Integer, Integer> o2) {
 return o1.getValue() - o2.getValue();
 }
 });
 //遍历排序好的list，一定要放进LinkedHashMap，因为只有LinkedHashMap是根据插入顺序进行存储
 LinkedHashMap<Integer, Integer> linkedHashMap = new LinkedHashMap<>();
 for (Map.Entry<Integer, Integer> e : entryList) {
 linkedHashMap.put(e.getKey(), e.getValue());
 }
 for (Map.Entry<Integer, Integer> e : entryList) {
 if (times == 0) {
 x_times.put(e.getKey(), 0);
 } else if (times == 1) {
 x_times.put(e.getKey(), 1);
 } else if (times == 2) {
 x_times.put(e.getKey(), 1);
 } else if (times == 3) {
 x_times.put(e.getKey(), 2);
 }
 times++;
 }
 //System.out.println(min_key+" "+key+" "+mid_key+" "+max_key);
 /**
 * 打印计算过程
 */
 String str_ten = "";
 for (int i = 0; i < 4; i++) {
 str_ten += "个体编号："+(i+1)+"\t" +
 "(" + xx[i][0] + ", " + xx[i][1] + ")" + "\t" + "适应度："
 + listFlag.get(i) + "\t" + "占总数的百分比：" + x_DaXiao.get(i)
 + ",选择次数：" + x_times.get(i) + "\n";
 }
 System.out.print(str_ten);
 System.out.println("最大的适应度为：" + result);
 }
 // 根据选择结果重新布局初始群体
 public static int[][] refreshXX() {
 int [][]xx_temp = new int[4][2];
 int flag = 0;
 for (int i = 0; i < 4; i++) {
 int n = x_times.get(i);
 if (n != 0) {
 for (int j = 0; j < n; j++) {
 xx_temp[flag][0] = xx[i][0];
 xx_temp[flag][1] = xx[i][1];
 flag++;
 }
 }
 n=0;
 }
 return xx_temp;
 }
 // 选择算法
 public static void select(){
 System.out.println("进行选择运算：");
 // 选择初始群体
 if(ch4.sum==1) {
 xx = startX();
 }
 // 计算适应度占比
 Map<Integer, Integer> listFlag = countShiYingDu(xx);
 // 根据适应度占比进行选择
 selectXX(listFlag);
 System.out.println("获得新的群体");
 // 重新布局群体
 xx = refreshXX();
 printXX();
 }
 // 交叉算法
 public static void cross(){
 System.out.println("进行交叉运算  ：");
 System.out.println("交叉前个体：");
 str = toBinStr(xx);
 for(String i:str){
 System.out.print(i+"\t");
 }
 System.out.println();
 // 随机选择交叉点
 int cross1 = (int) (Math.random()*6);
 int cross2 = (int) (Math.random()*6);
 // 随机选择交叉群体
 int x1 = (int) (Math.random()*4);
 int x2 = (int) (Math.random()*4);
 // 防止x1==x2
 while(x1==x2){
 x2 = (int) (Math.random()*4);
 }
 System.out.print("配对情况：配对前："+(x1+1)+"="+str[x1]+"和"+(x2+1)+"=" + str[x2]+"进行配对，交叉点："+(cross1+1)+"\t");
 // 第一组进行交叉运算
 String str1 = str[x1];
 String str2 = str[x2];
 String str1_1,str1_2;
 str1_1 = str1.substring(0,cross1)+str2.substring(cross1);
 str1_2 = str2.substring(0,cross1)+str1.substring(cross1);
 str[x1] = str1_1;
 str[x2] = str1_2;
 System.out.println("配对后："+(x1+1)+"="+str[x1]+", "+(x2+1)+"="+str[x2]);
 // 找出剩下两个数
 int x3=0,x4=0;
 boolean flag = false;
 for(int i=0;i<4;i++){
 if(i!=x2&&i!=x1&&x3==0){
 x3 = i;
 flag = true;
 }
 else if(i!=x2&&i!=x1&&flag){
 x4 = i;
 }
 }
 System.out.print("配对情况：配对前："+(x3+1)+"="+str[x3]+"和"+(x4+1)+"=" + str[x4]+"进行配对，交叉点："+(cross2+1)+"\t");
 // 第二组进行交叉运算
 String str2_1,str2_2;
 String str3 = str[x3];
 String str4 = str[x4];
 str2_1 = str3.substring(0,cross2)+str4.substring(cross2);
 str2_2 = str4.substring(0,cross2)+str3.substring(cross2);
 str[x3] = str2_1;
 str[x4] = str2_2;
 System.out.println("配对后："+(x3+1)+"="+str[x3]+", "+(x4+1)+"="+str[x4]);
 // 改变群体
 xx = toStrTen(str);
 System.out.println("交叉后个体：");
 printXX();
 }
 // 变异算法
 public static void variation(){
 System.out.println("进行变异算法：");
 // 群体二进制表示集合
 String str[] = toBinStr(xx);
 // 变异前
 List<String> listStr = new ArrayList<String>(Arrays.asList(str));
 // 随机确定变异点
 int var[] = new int[4];
 for(int i=0;i<4;i++){
 int num_var = (int) (Math.random()*3);
 var[i] = num_var;
 char[] arr = str[i].toCharArray();
 if(arr[num_var] == '0')
 arr[num_var] = '1';
 else
 arr[num_var] = '0';
 str[i] = "";
 for(char j:arr){
 str[i] += j;
 }
 }
 for(int i=0;i<4;i++){
 System.out.print("个体编号："+(i+1)+"\t"+listStr.get(i)+"\t变异点："+(var[i]+1)+"\t变异结果："+str[i].toString()+"\n");
 }
 // 再将变异后的群体转化为十进制。
 xx = toStrTen(str);
 sum++;
 System.out.println("第"+sum+"代群体为：");
 printXX();
 }
 // 二进制显示数字
 public static String num_0b(int num){
 String str = Integer.toBinaryString(num);
 if(str.length()<3&&num>4){
 if(str.length()<2)
 str+="0";
 str+="0";
 }
 else if(str.length()<3&&num<4){
 if(str.length()<2){
 str = "00" + str.substring(0,str.length());
 }
 else
 str = "0" + str.substring(0,str.length());
 }
 return str;
 }
 // 群体二进制表示
 public static String[] toBinStr(int [][]xx){
 for (int i=0;i<4;i++){
 str[i] = num_0b(xx[i][0]) + num_0b(xx[i][1]);
 }
 return str;
 }
 // 群体二进制转十进制
 public static int[][] toStrTen(String [] str){
 for(int i=0;i<4;i++){
 xx[i][0] = Integer.parseInt(str[i].substring(0,3),2);
 xx[i][1] = Integer.parseInt(str[i].substring(3),2);
 }
 return xx;
 }
 // 判断是否找到最优解
 public static boolean checkStr(String [] str){
 boolean flag = false;
 if(str[0]!=null) {
 for (int i = 0; i < 4; i++) {
 if (str[i].equals("111111")) {
 flag = true;
 result = 5*7*7;
 System.out.println("已经找到最大的适应度："+result);
 break;
 }
 }
 }
 return flag;
 }
 // 打印十进制初始群体
 public static void printXX(){
 String str_ten = "";
 for(int i=0;i<4;i++){
 str_ten += "(" + xx[i][0]+", " + xx[i][1]+")" + "\t";
 }
 System.out.println(str_ten);
 }
}

五．实验结果

5.1 实验输入和输出

输入无：

输出：此处输出比较多

----遗传算法----

第1代运算过程：

进行选择运算：

随机初始化群体：

(5, 0) (1, 3) (6, 3) (1, 5)

个体编号：1 (5, 0) 适应度：50 占总数的百分比：0.2,选择次数：1

个体编号：2 (1, 3) 适应度：29 占总数的百分比：0.11,选择次数：0

个体编号：3 (6, 3) 适应度：99 占总数的百分比：0.39,选择次数：2

个体编号：4 (1, 5) 适应度：77 占总数的百分比：0.3,选择次数：1

最大的适应度为：99

获得新的群体

(5, 0) (6, 3) (6, 3) (1, 5)

进行交叉运算 ：

交叉前个体：

101000 110011 110011 001101

配对情况：配对前：4=001101和1=101000进行配对，交叉点：4 配对后：4=001000, 1=101101

配对情况：配对前：2=110011和3=110011进行配对，交叉点：3 配对后：2=110011, 3=110011

交叉后个体：

(5, 5) (6, 3) (6, 3) (1, 0)

进行变异算法：

个体编号：1 101101 变异点：3 变异结果：100101

个体编号：2 110011 变异点：2 变异结果：100011

个体编号：3 110011 变异点：3 变异结果：111011

个体编号：4 001000 变异点：2 变异结果：011000

第2代群体为：

(4, 5) (4, 3) (7, 3) (3, 0)

第2代运算过程：

进行选择运算：

个体编号：1 (4, 5) 适应度：107 占总数的百分比：0.35,选择次数：1

个体编号：2 (4, 3) 适应度：59 占总数的百分比：0.19,选择次数：1

个体编号：3 (7, 3) 适应度：125 占总数的百分比：0.4,选择次数：2

个体编号：4 (3, 0) 适应度：18 占总数的百分比：0.06,选择次数：0

最大的适应度为：125

获得新的群体

(4, 5) (4, 3) (7, 3) (7, 3)

进行交叉运算 ：

交叉前个体：

100101 100011 111011 111011

配对情况：配对前：4=111011和2=100011进行配对，交叉点：1 配对后：4=100011, 2=111011

配对情况：配对前：3=111011和1=100101进行配对，交叉点：5 配对后：3=111001, 1=100111

交叉后个体：

(4, 7) (7, 3) (7, 1) (4, 3)

进行变异算法：

个体编号：1 100111 变异点：3 变异结果：101111

个体编号：2 111011 变异点：3 变异结果：110011

个体编号：3 111001 变异点：2 变异结果：101001

个体编号：4 100011 变异点：2 变异结果：110011

第3代群体为：

(5, 7) (6, 3) (5, 1) (6, 3)

第3代运算过程：

进行选择运算：

个体编号：1 (5, 7) 适应度：197 占总数的百分比：0.44,选择次数：2

个体编号：2 (6, 3) 适应度：99 占总数的百分比：0.22,选择次数：1

个体编号：3 (5, 1) 适应度：53 占总数的百分比：0.12,选择次数：0

个体编号：4 (6, 3) 适应度：99 占总数的百分比：0.22,选择次数：1

最大的适应度为：197

获得新的群体

(5, 7) (5, 7) (6, 3) (6, 3)

进行交叉运算 ：

交叉前个体：

101111 101111 110011 110011

配对情况：配对前：1=101111和3=110011进行配对，交叉点：1 配对后：1=110011, 3=101111

配对情况：配对前：2=101111和4=110011进行配对，交叉点：1 配对后：2=110011, 4=101111

交叉后个体：

(6, 3) (6, 3) (5, 7) (5, 7)

进行变异算法：

个体编号：1 110011 变异点：2 变异结果：100011

个体编号：2 110011 变异点：1 变异结果：010011

个体编号：3 101111 变异点：1 变异结果：001111

个体编号：4 101111 变异点：3 变异结果：100111

第4代群体为：

(4, 3) (2, 3) (1, 7) (4, 7)

第4代运算过程：

进行选择运算：

个体编号：1 (4, 3) 适应度：59 占总数的百分比：0.14,选择次数：1

个体编号：2 (2, 3) 适应度：35 占总数的百分比：0.08,选择次数：0

个体编号：3 (1, 7) 适应度：149 占总数的百分比：0.35,选择次数：1

个体编号：4 (4, 7) 适应度：179 占总数的百分比：0.42,选择次数：2

最大的适应度为：179

获得新的群体

(4, 3) (1, 7) (4, 7) (4, 7)

进行交叉运算 ：

交叉前个体：

100011 001111 100111 100111

配对情况：配对前：1=100011和3=100111进行配对，交叉点：4 配对后：1=100111, 3=100011

配对情况：配对前：2=001111和4=100111进行配对，交叉点：6 配对后：2=001111, 4=100111

交叉后个体：

(4, 7) (1, 7) (4, 3) (4, 7)

进行变异算法：

个体编号：1 100111 变异点：1 变异结果：000111

个体编号：2 001111 变异点：3 变异结果：000111

个体编号：3 100011 变异点：2 变异结果：110011

个体编号：4 100111 变异点：1 变异结果：000111

第5代群体为：

(0, 7) (0, 7) (6, 3) (0, 7)

第5代运算过程：

进行选择运算：

个体编号：1 (0, 7) 适应度：147 占总数的百分比：0.27,选择次数：1

个体编号：2 (0, 7) 适应度：147 占总数的百分比：0.27,选择次数：1

个体编号：3 (6, 3) 适应度：99 占总数的百分比：0.18,选择次数：0

个体编号：4 (0, 7) 适应度：147 占总数的百分比：0.27,选择次数：2

最大的适应度为：147

获得新的群体

(0, 7) (0, 7) (0, 7) (0, 7)

进行交叉运算 ：

交叉前个体：

000111 000111 000111 000111

配对情况：配对前：1=000111和2=000111进行配对，交叉点：1 配对后：1=000111, 2=000111

配对情况：配对前：3=000111和4=000111进行配对，交叉点：6 配对后：3=000111, 4=000111

交叉后个体：

(0, 7) (0, 7) (0, 7) (0, 7)

进行变异算法：

个体编号：1 000111 变异点：2 变异结果：010111

个体编号：2 000111 变异点：3 变异结果：001111

个体编号：3 000111 变异点：3 变异结果：001111

个体编号：4 000111 变异点：1 变异结果：100111

第6代群体为：

(2, 7) (1, 7) (1, 7) (4, 7)

第6代运算过程：

进行选择运算：

个体编号：1 (2, 7) 适应度：155 占总数的百分比：0.25,选择次数：1

个体编号：2 (1, 7) 适应度：149 占总数的百分比：0.24,选择次数：0

个体编号：3 (1, 7) 适应度：149 占总数的百分比：0.24,选择次数：1

个体编号：4 (4, 7) 适应度：179 占总数的百分比：0.28,选择次数：2

最大的适应度为：179

获得新的群体

(2, 7) (1, 7) (4, 7) (4, 7)

进行交叉运算 ：

交叉前个体：

010111 001111 100111 100111

配对情况：配对前：2=001111和1=010111进行配对，交叉点：6 配对后：2=001111, 1=010111

配对情况：配对前：3=100111和4=100111进行配对，交叉点：4 配对后：3=100111, 4=100111

交叉后个体：

(2, 7) (1, 7) (4, 7) (4, 7)

进行变异算法：

个体编号：1 010111 变异点：3 变异结果：011111

个体编号：2 001111 变异点：3 变异结果：000111

个体编号：3 100111 变异点：2 变异结果：110111

个体编号：4 100111 变异点：1 变异结果：000111

第7代群体为：

(3, 7) (0, 7) (6, 7) (0, 7)

第7代运算过程：

进行选择运算：

个体编号：1 (3, 7) 适应度：165 占总数的百分比：0.24,选择次数：1

个体编号：2 (0, 7) 适应度：147 占总数的百分比：0.22,选择次数：0

个体编号：3 (6, 7) 适应度：219 占总数的百分比：0.32,选择次数：2

个体编号：4 (0, 7) 适应度：147 占总数的百分比：0.22,选择次数：1

最大的适应度为：219

获得新的群体

(3, 7) (6, 7) (6, 7) (0, 7)

进行交叉运算 ：

交叉前个体：

011111 110111 110111 000111

配对情况：配对前：2=110111和4=000111进行配对，交叉点：1 配对后：2=000111, 4=110111

配对情况：配对前：3=110111和1=011111进行配对，交叉点：5 配对后：3=110111, 1=011111

交叉后个体：

(3, 7) (0, 7) (6, 7) (6, 7)

进行变异算法：

个体编号：1 011111 变异点：2 变异结果：001111

个体编号：2 000111 变异点：2 变异结果：010111

个体编号：3 110111 变异点：2 变异结果：100111

个体编号：4 110111 变异点：1 变异结果：010111

第8代群体为：

(1, 7) (2, 7) (4, 7) (2, 7)

第8代运算过程：

进行选择运算：

个体编号：1 (1, 7) 适应度：149 占总数的百分比：0.23,选择次数：0

个体编号：2 (2, 7) 适应度：155 占总数的百分比：0.24,选择次数：1

个体编号：3 (4, 7) 适应度：179 占总数的百分比：0.28,选择次数：2

个体编号：4 (2, 7) 适应度：155 占总数的百分比：0.24,选择次数：1

最大的适应度为：179

获得新的群体

(2, 7) (4, 7) (4, 7) (2, 7)

进行交叉运算 ：

交叉前个体：

010111 100111 100111 010111

配对情况：配对前：1=010111和2=100111进行配对，交叉点：1 配对后：1=100111, 2=010111

配对情况：配对前：3=100111和4=010111进行配对，交叉点：4 配对后：3=100111, 4=010111

交叉后个体：

(4, 7) (2, 7) (4, 7) (2, 7)

进行变异算法：

个体编号：1 100111 变异点：1 变异结果：000111

个体编号：2 010111 变异点：1 变异结果：110111

个体编号：3 100111 变异点：3 变异结果：101111

个体编号：4 010111 变异点：1 变异结果：110111

第9代群体为：

(0, 7) (6, 7) (5, 7) (6, 7)

第9代运算过程：

进行选择运算：

个体编号：1 (0, 7) 适应度：147 占总数的百分比：0.19,选择次数：0

个体编号：2 (6, 7) 适应度：219 占总数的百分比：0.28,选择次数：1

个体编号：3 (5, 7) 适应度：197 占总数的百分比：0.25,选择次数：1

个体编号：4 (6, 7) 适应度：219 占总数的百分比：0.28,选择次数：2

最大的适应度为：219

获得新的群体

(6, 7) (5, 7) (6, 7) (6, 7)

进行交叉运算 ：

交叉前个体：

110111 101111 110111 110111

配对情况：配对前：3=110111和2=101111进行配对，交叉点：3 配对后：3=111111, 2=100111

配对情况：配对前：4=110111和1=110111进行配对，交叉点：1 配对后：4=110111, 1=110111

交叉后个体：

(6, 7) (4, 7) (7, 7) (6, 7)

进行变异算法：

个体编号：1 110111 变异点：1 变异结果：010111

个体编号：2 100111 变异点：1 变异结果：000111

个体编号：3 111111 变异点：1 变异结果：011111

个体编号：4 110111 变异点：2 变异结果：100111

第10代群体为：

(2, 7) (0, 7) (3, 7) (4, 7)

第10代运算过程：

进行选择运算：

个体编号：1 (2, 7) 适应度：155 占总数的百分比：0.24,选择次数：1

个体编号：2 (0, 7) 适应度：147 占总数的百分比：0.23,选择次数：0

个体编号：3 (3, 7) 适应度：165 占总数的百分比：0.26,选择次数：1

个体编号：4 (4, 7) 适应度：179 占总数的百分比：0.28,选择次数：2

最大的适应度为：179

获得新的群体

(2, 7) (3, 7) (4, 7) (4, 7)

进行交叉运算 ：

交叉前个体：

010111 011111 100111 100111

配对情况：配对前：2=011111和1=010111进行配对，交叉点：6 配对后：2=011111, 1=010111

配对情况：配对前：3=100111和4=100111进行配对，交叉点：5 配对后：3=100111, 4=100111

交叉后个体：

(2, 7) (3, 7) (4, 7) (4, 7)

进行变异算法：

个体编号：1 010111 变异点：2 变异结果：000111

个体编号：2 011111 变异点：1 变异结果：111111

个体编号：3 100111 变异点：2 变异结果：110111

个体编号：4 100111 变异点：2 变异结果：110111

第11代群体为：

(0, 7) (7, 7) (6, 7) (6, 7)

已经找到最大的适应度：245

Process finished with exit code 0

5.2 实验截图

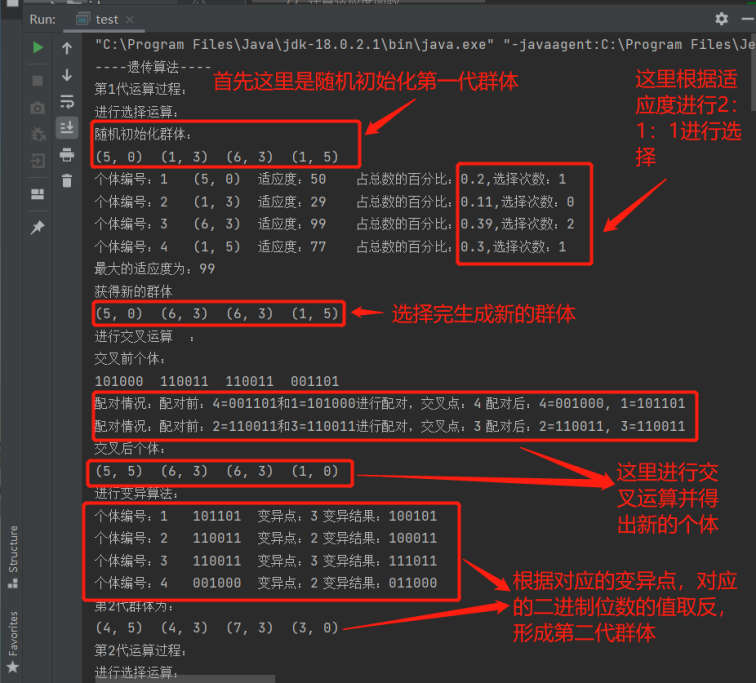
六、实验结果分析与讨论

从上图可以知道，历经10次迭代，最后终于在第十一代群体产生了111111，也就可以得出最大的适应度即为245.其实还有一些实验结果迭代的次数比较大。随机性比较大，无法确定哪一代能产生最大适应度的群体。

我正在参与2024腾讯技术创作特训营第五期有奖征文，快来和我瓜分大奖！