Acwing数学与简单DP(二)
摘花生
最后一步,有两种可能:
- 从上面走
- 从下面走
也就是max(dp[i-1][j],dp[i][j-1]),再加上最后一个位置的值。
#include"bits/stdc++.h"
using namespace std;
int dp[110][110];
int T, R, C;
int main() {
cin >> T;
while (T--) {
cin >> R >> C;
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
cin >> dp[i][j];
}
}
for (int i = 1; i <= R; i++) {
for (int j = 1; j <= C; j++) {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + dp[i][j];
}
}
cout << dp[R][C] << endl;
}
return 0;
}最长上升子序列
最后一步,有两种可能:
- 最后一个元素可以与之前的元素构成上升子序列,长度为已知长度+1
- 最后一个元素没有可组合的子序列,长度为1
最长上升子序列的结束位置未必是最后一个元素,因此需要遍历长度数组,选取最大值。 需要存储:
- 指向序列某个元素时,截至该元素的最长子序列长度
这可以通过创建一个与原序列等长的dp数组实现。 该数组中,与原序列,下标相同的元素,的值,就是原序列截止到该元素处,的最长上升子序列长度。 需要二层循环,平方复杂度:
- 外层循环,更新dp数组的第
i个元素。 - 更新到第
i个元素时,需要查找前i-1个元素。如果前i-1个元素中,某个元素的值,小于当前要更新的元素的值,那么就可以把当前元素接在这个元素后面。dp[i]的值就是dp[该元素的下标]+1。前i-1个元素可能存在多个小于当前元素的元素,取最大的构成最长子序列。
最后遍历长度数组,求最大值。
#include"bits/stdc++.h"
using namespace std;
int a[1010], f[1010];
int n;
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) scanf("%d", a + i);
for (int i = 1; i <= n; i++) {
f[i] = 1;
for (int j = 1; j < i; j++)
if (a[j] < a[i]) {
f[i] = max(f[i], f[j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; i++)res = max(res, f[i]);
cout << res;
return 0;
}地宫取宝
原题链接:https://www.acwing.com/problem/content/description/1214/
限制:
- 只能往下或往右走
- 递增地取
- 刚好取k个数
数据范围,很小,允许多层循环。意味着有多个维度。
f(i,j,k,c)四个维度分别表示:
i,j:坐标k:当前取多少个c:最后一件的价值,由于是递增地取,也就是当前取的最大值

取的条件,w[i,j]的值等于c。对,是等于,而不是大于。因为f(i,j,k,c)中的c指的是最后一件的值,也就是当前元素的值。
如果不选,就直接从上一步把状态k和c转移过来。
如果选了,那上一步就应该选了k-1个物品,而且最大值只能是[1,c-1],把这些状态的方案数累加。
从集合的角度分析DP,本题可以描述为:

因为涉及四层循环,四重DP,所以比较费解。更详细的分析过程在代码下面。
#include"bits/stdc++.h"
using namespace std;
const int MOD = 1000000007;
int w[55][55];
int dp[55][55][13][14];
int n, m, k;
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%d", &w[i][j]);
w[i][j]++;
}
}
dp[1][1][1][w[1][1]] = 1;
dp[1][1][0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (i == 1 && j == 1)continue;
for (int u = 0; u <= k; u++) {
for (int v = 0; v <= 13; v++) {
int &val = dp[i][j][u][v];
val = (val + dp[i - 1][j][u][v]) % MOD;
val = (val + dp[i][j - 1][u][v]) % MOD;
if (u > 0 && v == w[i][j]) {
for (int c = 0; c < v; c++) {
val = (val + dp[i - 1][j][u - 1][c]) % MOD;
val = (val + dp[i][j - 1][u - 1][c]) % MOD;
}
}
}
}
}
}
int res = 0;
for (int i = 0; i <= 13; i++)res = (res + dp[n][m][k][i]) % MOD;
cout << res;
return 0;
}边界情况:第一个元素的选取状态。由于DP是集合划分,本题有四个维度,就要分别考虑四个维度的情况。
第一个元素,坐标为(1,1),i和j都只能为1.
有选和不选两种状态,k表示当前已选取的元素个数,k有1和0两种状态。
c表示当前选取的最大值。如果选了,那么最大值就是w[i][j],如果没选,那么是没有最大值的,需要自定义一个,数据范围是[0,12],如果设置为0,由于后续判断的依据是“大于”而非“大于等于”,所以如果之后出现了0,那么将错过该位置。所有(1,1)的位置在未选取时应设置为-1或其他小于0的数。
而数组下标从0开始,那么需要添加一个偏移量1。偏移量所在的维度c应该整体偏移,因此代码中该维度的范围是[1,13],并且在读入w[i][j]时,进行了++操作。
DP的状态计算,也就是集合划分,主要是参考最后一步。
最后有两种情况,选最后也就是当前元素、不选最后也就是当前元素。
如果不选,那么目前这种方案的k和c不变,与上一步相同,状态值可以从上一步转移过来。如果是从左边过来,那就是dp[i][j][u][v]+=dp[i - 1][j][u][v]。如果是从上面过来,那就是+=dp[i][j-1][u][v].在此省略了取模操作。
为什么要+=,而不是直接用=赋值?当前DP问题的解决方案是基于集合,集合有多种划分,目前的最后一步,有多种情况,把各种情况的方案数加起来,才是集合的值。
如果选,那么需要先判断是否符合可选的条件。k表示当前取多少个,在上面的代码中用的是u。如果值为0,那说明没有取值,当然也就没选取最后一个。DP其实还是在枚举,不过是聪明的枚举,考虑了利用部分条件。c在集合中,表示当前选取的最大元素,因为是递增选取,当确定要选择当前元素时,那么c的值应该当前元素的值。
为什么要判断c==w[i][j]?因为DP的过程还是在枚举,枚举四个维度的所有可能情况。当前枚举的情况未必是符合状态表示的。
如果确定了选取当前元素。那么i,j,k三个维度容易确定:
i和j根据从左边来还是从上边来。k表示元素个数,在选之前,是有k-1个元素,只能从k-1所在的维度中选取。c表示最大值,在选之前,最大值可能是1...c-1中的任何一种情况,枚举所有情况。
if (u > 0 && v == w[i][j]) {
for (int c = 0; c < v; c++) {
val = (val + dp[i - 1][j][u - 1][c]) % MOD;
val = (val + dp[i][j - 1][u - 1][c]) % MOD;
}
}因为会多次修改dp[i][j][u][v],所有创建了对该内存位置的引用&val,对val的修改会影响指向的内存数据。
每次运算都在取模,最多只能加两个数。如果加三个再取模,有可能超出范围报错。
参考
波动数列
第一项设为x,第二项设为x+d1,第二项设为x+d1+d2…
每一个d都只有两种取值:+a,-b
n项加起来的和是s:nx+(n-1)d1+(n-2)d2+...+dn-1=s
原序列所有不同的方案,是由变量决定的。
第一个变量是x:属于任意整数
之后的di:只有两种取值
由于x取法太多,没有限制。并且这是一个等式,可以去掉一个变量,用n-1个变量表示被去掉的那个。
由于是整数序列,x也是整数,所以
应该是n的倍数。
等价于:
s与
模n同余
而s可能是负数(数据范围有给),取模可能是负数。需要实现一个函数,求正余数。
如果最后一项选择+a,那么:
s与
模n同余。
系数,和,下标,的关系是:和等于n。在选择a时,a是最后一项,因此倒数第二项变成了
,而非之前出现的
,此时a就是
。
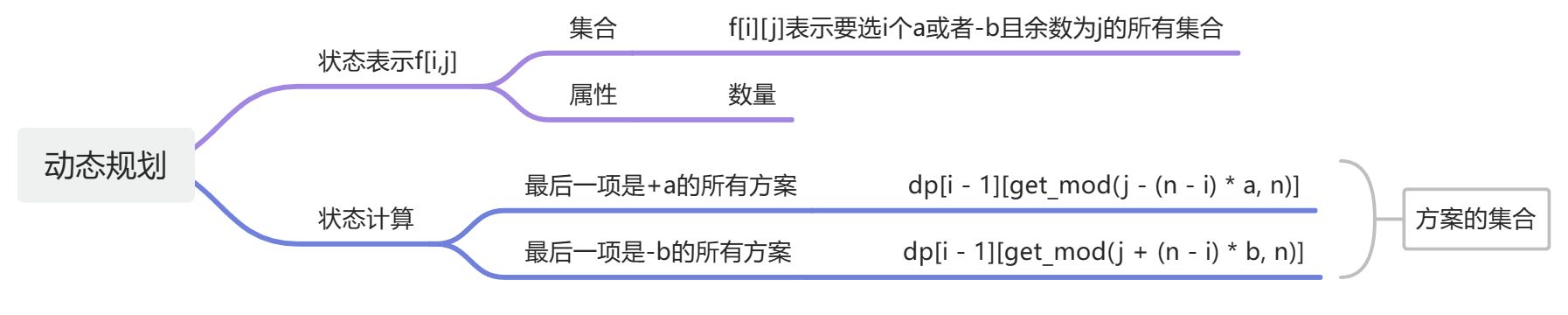
因为系数和下标发生了变动,为了便于理解,设前n-1项的和为C。
对于f[i][j]这个集合,从f[i-1][C%n]状态转移过来的时候,如果选择+a,那么第一个维度,含义是选择的个数,自然+1,也就是[i]。
第二个维度,就是(C+a)%n,等于j。
也就是说:j与C+a模n同余。
那么j-a与C模n同余。
状态转移时,第二个维度的含义是模n的余数。要求转移之前的值,也就是求C%n,那么就可以转换成求(j-a)%n。j-a可能是负数,求出来的是负余数,不在数组下标范围之内。需要求正余数。
也就得到这样一个式子:dp[i][j] = (dp[i - 1][get_mod(j - a, n)] + dp[i - 1][get_mod(j + b, n)]) % MOD;其中get_mod用于求正余数。
但这个状态转移方程是无法通过AC的。
因为上文中:
s与
模n同余
- 模
n的时候,右式有n项。
在从n-1转移到n时,第二维度值是
在从n-2转移到n-1时,第二维度值是
也就是说,di前面是有系数的。
这个状态转移方程:dp[i][j] = (dp[i - 1][get_mod(j - a, n)] + dp[i - 1][get_mod(j + b, n)]) % MOD;中{a,b}的系数是1只考虑了最后一步,也就是从n-1转移到n的情况。
在前n-1项状态转移时,应将系数考虑在内。带系数做减法,才能求出正确的正余数。
系数,与,下标,的和是n。因此有:
#include"bits/stdc++.h"
using namespace std;
int n, s, a, b;
int dp[1010][1010];
int MOD = 100000007;
int get_mod(int a, int b) {
return (a % b + b) % b;
}
int main() {
cin >> n >> s >> a >> b;
dp[0][0] = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = (dp[i - 1][get_mod(j - (n - i) * a, n)] + dp[i - 1][get_mod(j + (n - i) * b, n)]) % MOD;
}
}
cout << dp[n - 1][get_mod(s, n)];
return 0;
}本文参与 腾讯云自媒体同步曝光计划,分享自作者个人站点/博客。
原始发表:2024-02-28,如有侵权请联系 cloudcommunity@tencent.com 删除
评论
登录后参与评论
推荐阅读
目录


