算法妙妙屋-------1.递归的深邃回响：C++ 算法世界的优雅之旅

hope kc

发布于 2024-11-21 14:45:10

17400

代码可运行

文章被收录于专栏：学习学习

运行总次数：0

代码可运行

前言：

递归是一种在算法中广泛应用的思想，其主体思想是通过将复杂的问题分解为更简单的子问题来求解。具体而言，递归通常包括以下几个要素：

基本情况（Base Case）：每个递归算法必须有一个或多个基本情况，用于定义何时停止递归。基本情况是问题的 最小实例 ，直接返回结果，不再进行进一步的递归。
递归情况（Recursive Case）：当问题不是 基本情况 时，递归算法会将问题 拆分成更小的子问题 。算法会调用自身来解决这些子问题，通常会在调用中传递参数以反映问题的简化。
合并结果（Combining Results）：在递归调用返回后，算法 ***会将子问题的结果合并***，以得到原始问题的解。

递归的优势在于其代码通常更简洁且易于理解，尤其是在处理分治问题（如排序、搜索等）时。然而，递归也可能导致栈溢出问题，因为每次调用都会在栈上占用空间，因此在使用时需要考虑调用深度和性能优化。

下面，我们就用习题来给大家做解释吧!

1. 汉诺塔（easy）（非常经典）

题目链接：汉诺塔

递归函数流程：

当前问题规模为n=1时，直接将A中的最上⾯盘⼦挪到C中并返回；
递归将A中最上⾯的n-1个盘⼦挪到B中；
将A中最上⾯的⼀个盘⼦挪到C中；
将B中上⾯n-1个盘⼦挪到C中。

解题思路：

先把n-1盘全部移到B上去
再把第n盘移到C上去
再把n-1盘移到C上去

代码如下：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        dfs(A, B, C,A.size());
    }


    void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n)
    {
        if(n==1)
        {
            C.push_back(A.back());
            A.pop_back();
            return;
        }

         dfs(A, C, B,n-1);//这一步是为了将除了最大的盘子留下外，其他全部转移到B盘
         C.push_back(A.back());
         A.pop_back();//这一步是为了把最大的盘子转移到C盘
         dfs(B, A, C,n-1);//这一步是进行递归，B盘变成了A盘，A盘变成了B盘,目的是为了将其他盘全部转移到C盘
    }
};

2.合并两个有序链表（easy）

题目链接：合并两个有序链表题目描述：将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

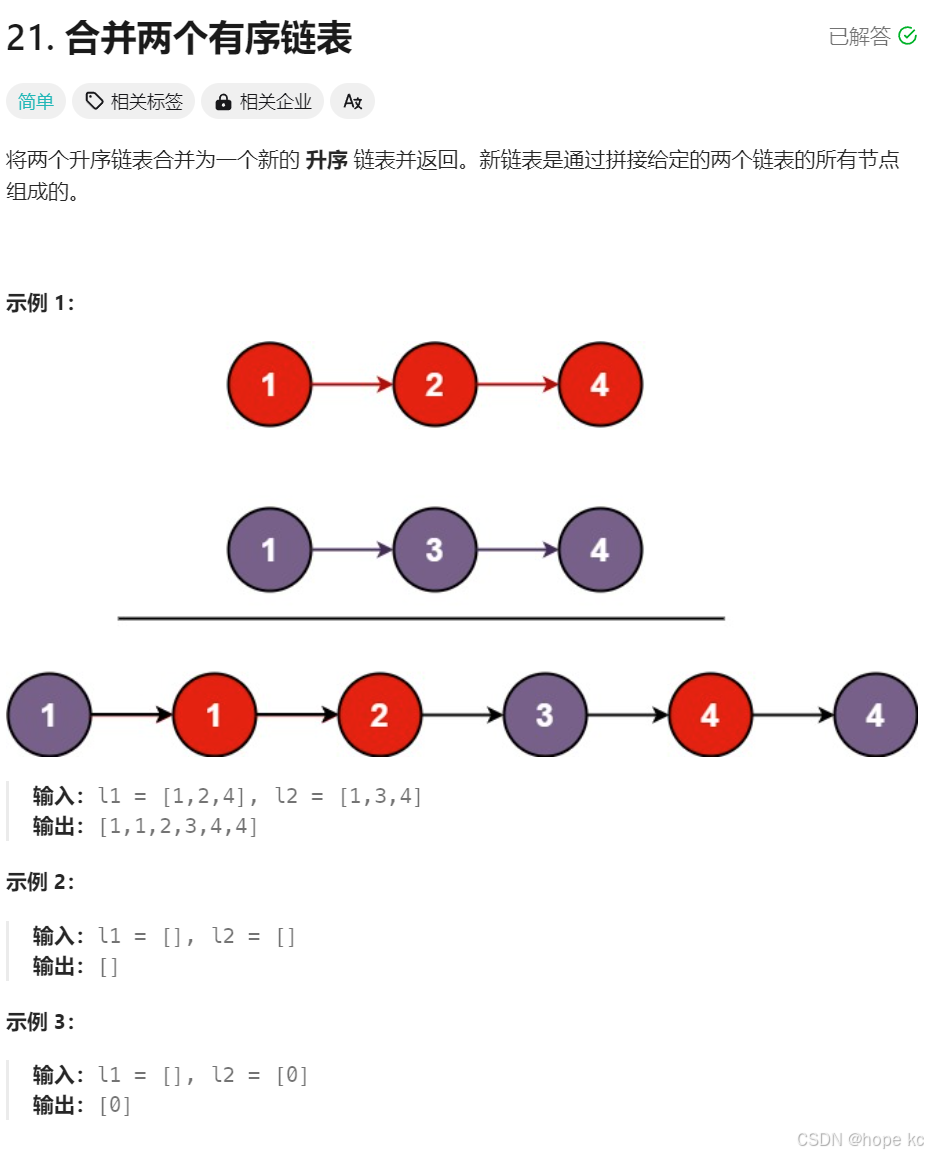
算法思路：

递归函数的含义：交给你两个链表的头结点，你帮我把它们合并起来，并且返回合并后的头结点；
函数体：选择两个头结点中较⼩的结点作为最终合并后的头结点，然后将剩下的链表交给递归函数去处理；
递归出⼝：当某⼀个链表为空的时候，返回另外⼀个链表。

注意注意注意：链表的题⼀定要画图，搞清楚指针的操作！

解题思路：

判断某一个参数是否为空，为空则返回 另一个参数
如果两者都不为空，则 比较l1的元素和l2元素的大小
元素***小的节点留下***，并把 该节点的next 和 另一节点 作为下一轮递归函数的参数
下一轮递归函数的 返回值变为该节点的next
返回该节点 (小的那一个)

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
         if(list1==NULL)
         {
            return list2;
         }

         if(list2==NULL)
          {
            return list1;
          }

        if(list1->val<=list2->val)
        {
            list1->next=mergeTwoLists(list1->next, list2);
            return list1;
        }
        else
        {
            list2->next=mergeTwoLists(list1, list2->next);
            return list2;
        }
    }
};

3. 反转链表（easy）

题目链接：反转链表

题⽬描述：

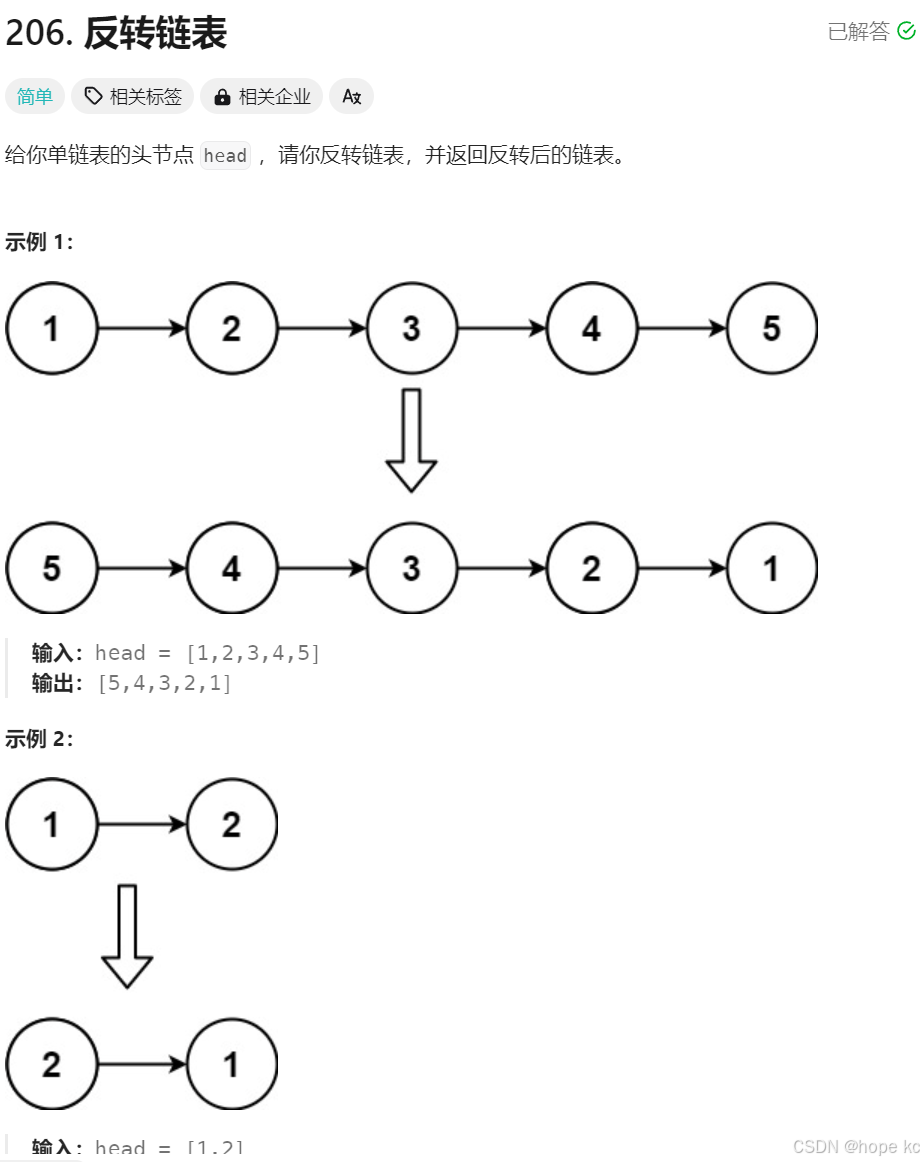
解题思路：

先通过一层循环找到尾，因为 尾就是新的头节点
找到尾之后，把 head 做为参数，传给递归函数

递归函数：

如果head->next为空，直接返回head

否则，将head->next作为参数进入下一次递归
***下一次递归函数的返回值-***>next=head；
head->next=nullptr;
返回head

class Solution {
public:

     ListNode* reverseL(ListNode* head)
     {
       if(head->next==nullptr)
        return head;
     
       else
       { 
        reverseL(head->next)->next=head;
        head->next=nullptr;
        return head;
       }
     }


    ListNode* reverseList(ListNode* head) {
        ListNode* it=head;
        if(head==nullptr)
        return head;
        while(it->next!=nullptr)
        {
            it=it->next;
        }
        reverseL(head);
        return it;
    }
};

4.两两交换链表中的节点（medium）

题目链接：两两交换链表中的节点题目描述：

解题思路：

如果（1）head为空，返回nullptr
如果（2）head->next==nullptr,返回head
否则（3）将head->next->next作为参数进行下一次递归
递归的返回值赋值给head->next->next
交换head和head->next
返回原来的head->next

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {


         if(head==nullptr)
        {
            return nullptr;
        }

         else if(head->next==nullptr)
        {
            return head;
        }

         
            head->next->next=swapPairs(head->next->next);
            
            ListNode* it=head->next;
            head->next=head->next->next;
            it->next=head;//交换head和head->next

            return it;
    }
};