2024-12-01：单面值组合的第 K 小金额。用go语言，给定一个整数数组 coins，表示不同面值的硬币，同时给出一个整数

福大大架构师每日一题

发布于 2024-12-03 21:13:15

13200

代码可运行

运行总次数：0

代码可运行

2024-12-01：单面值组合的第 K 小金额。用go语言，给定一个整数数组 coins，表示不同面值的硬币，同时给出一个整数 k。你可以使用任意数量的这些硬币，但不能将不同面值的硬币组合在一起。请返回可以用这些硬币构成的第 k 个最小金额。

1 <= coins.length <= 15。

1 <= coins[i] <= 25。

1 <= k <= 2 * 10^9

输入：coins = [5,2], k = 7。

输出：12。

解释：给定的硬币可以制造以下金额：

5元硬币产生5的倍数：5, 10, 15, 20等。

2元硬币产生2的倍数：2, 4, 6, 8, 10, 12等。

所有硬币合起来可以产生：2, 4, 5, 6, 8, 10, 12, 14, 15等，12是第7个数。

答案2024-12-01：

chatgpt[1]

题目来自leetcode3116。

大体步骤如下：

1.对给定的硬币面值数组 coins 进行排序，以便后续处理。

2.创建一个空数组 a 用于存放不同面值的硬币。

3.遍历排序后的硬币数组，对于每一个硬币 x：

• 遍历数组 a 中的每个元素 y，检查是否 x 能整除 y，如果可以，则跳过该硬币 x。
• 如果 x 不能整除任何已选中的硬币，则将 x 加入数组 a。

4.计算数组 a 的所有子集的最小公倍数，并根据每个子集包含硬币的数量对最小公倍数的正负号进行调整。

5.使用二进制位运算构建所有子集的最小公倍数。

6.使用二进制计数方法判断对应子集的硬币数量是否大于等于 k。

7.输出第 k 个最小金额。

总体而言，这个解决方案涉及对硬币面值进行排序、计算最小公倍数、二进制位运算等操作。时间复杂度取决于硬币面值数组的长度和 k，为 O(2^n * n + n^2 * log(n))，其中 n 为硬币数量。

额外空间复杂度为 O(2^n)。

Go完整代码如下：

package main

import(
"fmt"
"slices"
"sort"
"math/bits"
)

func findKthSmallest(coins []int, k int)int64{
    slices.Sort(coins)
    a := coins[:0]
next:
for _, x :=range coins {
for _, y :=range a {
if x%y ==0{
continuenext
}
}
        a =append(a, x)
}

    subsetLcm :=make([]int,1<<len(a))
    subsetLcm[0]=1
for i, x :=range a {
        bit :=1<< i
for mask, l :=range subsetLcm[:bit]{
            subsetLcm[bit|mask]= lcm(l, x)
}
}
for i :=range subsetLcm {
if bits.OnesCount(uint(i))%2==0{
            subsetLcm[i]*=-1
}
}

    ans := sort.Search(a[0]*k,func(m int)bool{
        cnt :=0
for _, l :=range subsetLcm[1:]{
            cnt += m / l
}
return cnt >= k
})
returnint64(ans)
}

func gcd(a, b int)int{
for a !=0{
        a, b = b%a, a
}
return b
}

func lcm(a, b int)int{
return a / gcd(a, b)* b
}

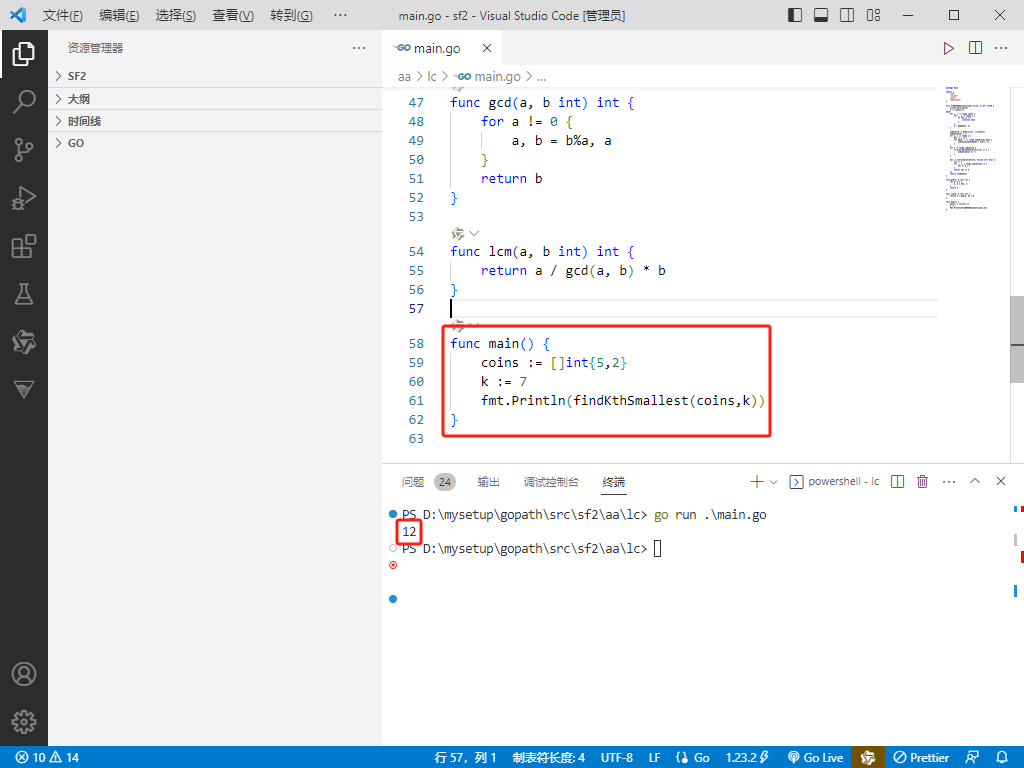
func main(){
    coins :=[]int{5,2}
    k :=7
    fmt.Println(findKthSmallest(coins,k))
}

Rust完整代码如下：

use std::cmp::Ordering;

fnfind_kth_smallest(coins:&[i32], k:i32)->i64{
letmut sorted_coins= coins.to_vec();
    sorted_coins.sort_unstable();

letmut filtered_coins=Vec::new();
'next:for&x in&sorted_coins {
for&y in&filtered_coins {
if x % y ==0{
continue'next;
}
}
        filtered_coins.push(x);
}

letn= filtered_coins.len();
letsubset_lcm_size=1<< n;
letmut subset_lcm=vec![1; subset_lcm_size];

for(i,&x)in filtered_coins.iter().enumerate(){
letbit=1<< i;
formaskin0..bit {
            subset_lcm[bit | mask]=lcm(subset_lcm[mask], x);
}
}

foriin0..subset_lcm_size {
if i.count_ones()%2==0{
            subset_lcm[i]*=-1;
}
}

letmax_search_value= filtered_coins[0]* k;
letmut low=1;
letmut high= max_search_value;

while low < high {
letmid=(low + high)/2;
letmut cnt=0;

for&l in&subset_lcm[1..]{
            cnt += mid / l;
}

if cnt >= k {
            high = mid;// If we have enough counts, we try smaller value
}else{
            low = mid +1;// If not enough, we go higher
}
}

    low asi64
}

fngcd(a:i32, b:i32)->i32{
letmut a= a;
letmut b= b;
while a !=0{
lettemp= b;
        b = a;
        a = temp % a;
}
    b
}

fnlcm(a:i32, b:i32)->i32{
    a /gcd(a, b)* b
}

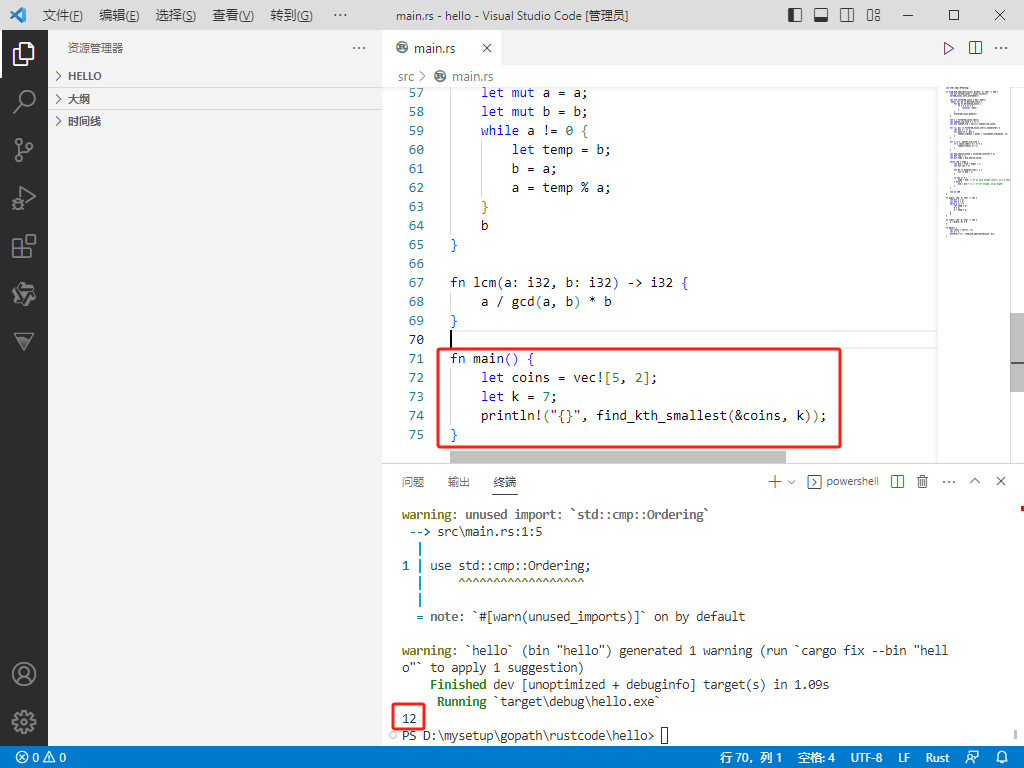
fnmain(){
letcoins=vec![5,2];
letk=7;
println!("{}",find_kth_smallest(&coins, k));
}