算法系列之回溯算法

在计算机科学领域,算法是解决问题的核心。回溯算法作为一种经典的算法设计技巧,以其试错和回退的思想,在解决许多复杂问题时展现出强大的能力。本文将深入探讨回溯算法,包括其核心概念、实现步骤、代码示例以及适用场景,帮助读者更好地理解和应用这一算法。
回溯算法概述
- 回溯算法
回溯算法(Backtracking Algorithm)是一种通过穷举来解决问题的方法,它的核心思想是从一个初始状态出发,暴力搜索所有可能的解决方案,遇到正确解将其记录,直到找到了所有的解或者尝试了所有的可能为止。
- 回溯算法的基本思想
回溯算法的核心思想可以概括为试错和回退:
- 试错: 从问题的初始状态出发,逐步构建候选解,尝试每一种可能的选择。
- 回退: 当发现当前选择无法达到目标状态时,回退到上一步,尝试其他选择,直到找到所有可能的解或确定无解。
- 回溯算法的适用场景
回溯算法通常适用于以下类型的问题:
- 组合问题: 从一组元素中找出所有满足条件的组合,例如子集、排列、组合数等。
- 约束满足问题: 在满足一定约束条件下,寻找所有可能的解,例如八皇后问题、数独等。
- 搜索问题: 在图或树等数据结构中搜索特定路径或目标,例如迷宫问题、图的着色问题等。
回溯算法的实现步骤
- 确定解空间
首先,需要明确问题的解空间,即所有可能的候选解。解空间通常可以用树形结构表示,每个节点代表一个候选解,边代表选择。
- 定义递归函数
使用递归函数来实现回溯算法。递归函数需要包含以下关键步骤:
- 选择: 在当前状态下,选择一个可行的选项。
- 递归: 进入下一层递归,尝试构建更完整的候选解。
- 回退: 如果当前选择无法达到目标状态,则回退到上一步,尝试其他选择。
- 剪枝优化
为了提高算法效率,可以使用剪枝技术,即在递归过程中提前排除不可能达到目标状态的分支,减少不必要的搜索。
Java 实现示例:全排列问题
- 描述:
给出一组数字,返回该组数字的所有排列 例如: [1,2,3]的所有排列如下 [1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1]. (以数字在数组中的位置靠前为优先级,按字典序排列输出。)
数据范围:数字个数 0<n≤6 要求:空间复杂度 O(n!) ,时间复杂度 O(n!)
- 示例:
示例1
输入:[1,2,3]
返回值:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例2
输入:[1]
返回值:[[1]]
- 分析
我们可以将搜索过程展开成一颗递归树,树中的每个节点代表当前的状态,从根节点开始,通过三轮选择后到达叶子节点,每个节点都对因一个排列。如下图所示:
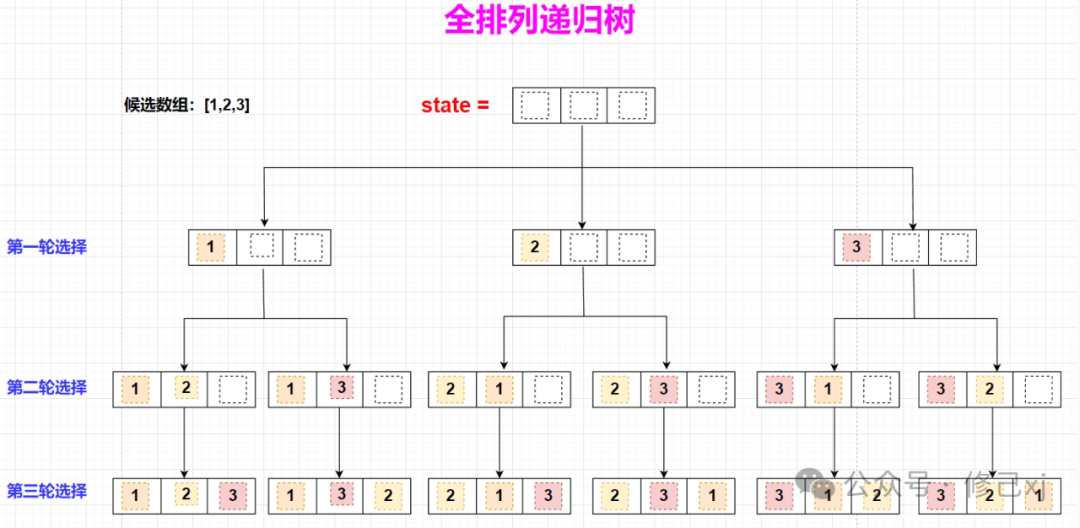
为了实现每个元素只被选择一次,我们引入了一个boolean的数组来标记当前元素是否已经选择,并基于它实现以下的剪枝操作。如下所示:
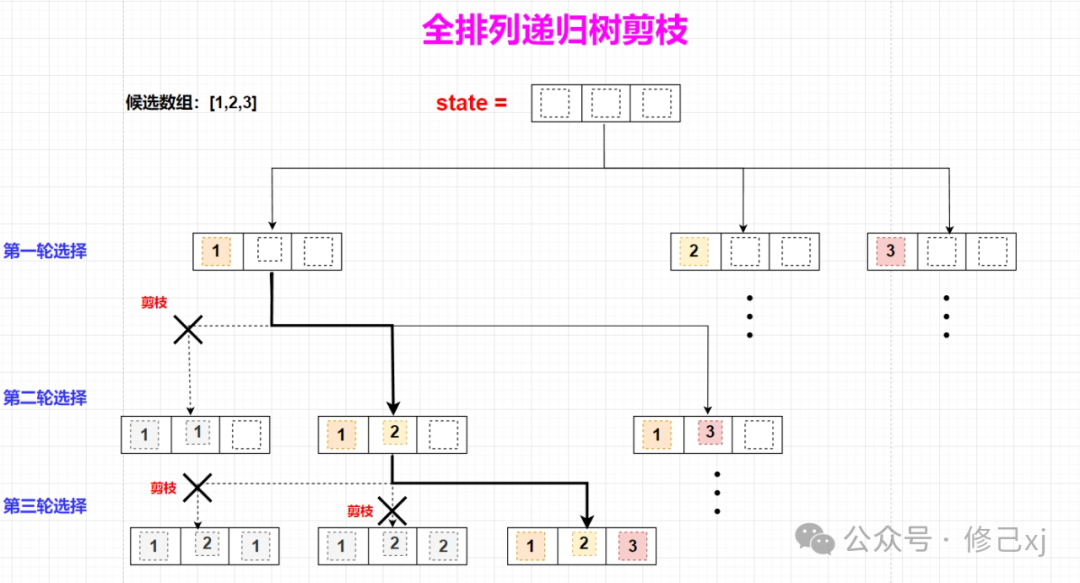
- 代码实现
public class Permutations {
/**
* 回溯法,全排列入口类
* @param nums
* @return
*/
public static List<List<Integer>> permute(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
//递归方法
backtrack(result, new ArrayList<>(),new boolean[nums.length], nums);
return result;
}
/**
* 回溯法,全排列递归方法
* @param result
* @param temp
* @param selected
* @param nums
*/
private static void backtrack(List<List<Integer>> result, List<Integer> temp, boolean[] selected, int[] nums) {
// 如果排列的数组长度为数组长度,则说明已经排列完成,将排列结果添加到结果集
if (temp.size() == nums.length) {
result.add(new ArrayList<>(temp));
return;
}
// 遍历数组,用数组的每个元素一次进行递归
for (int i=0 ; i < nums.length; i++) {
//剪枝:如果当前元素已经被使用过,则跳过
if (selected[i]) {
continue;
}
//排列的集合中添加当前元素
temp.add(nums[i]);
//将当前元素标记为已选则
selected[i] = true;
//递归进行下一轮选择
backtrack(result, temp, selected, nums);
//回退:撤销之前的选择
temp.removeLast();
//恢复之前的状态
selected[i] = false;
}
}
public static void main(String[] args) {
int[] nums = {1,2,3};
List<List<Integer>> result = permute(nums);
System.out.println(result);
}
}
总结
回溯算法是一种强大而灵活的算法设计技巧,适用于解决许多复杂的组合、约束满足和搜索问题。通过系统地构建候选解并在必要时回退,回溯算法能够有效地搜索解空间,找到所有可能的解。在实际应用中,结合剪枝等优化技术,可以进一步提高算法的效率。希望本文能够帮助读者更好地理解和应用回溯算法。


