地图导航的幕后英雄：图论如何改变出行？—全程动画可视化数据结构算法之图算法题目试炼

盛透侧视攻城狮

发布于 2025-03-24 11:02:55

13600

代码可运行

文章被收录于专栏：超前沿网络空间安全全栈学习宝典超前沿网络空间安全全栈学习宝典

运行总次数：0

代码可运行

本篇技术博文摘要 🌟🌟🌟

本文系统归纳了数据结构与算法中图论的核心知识点与实践方法，通过分层递进的结构帮助读者掌握关键技术。主要内容分为四大模块：
图的存储与基本操作
- 详解邻接矩阵与邻接表两种存储结构的实现原理，提供代码算法思路与核心代码实现（如6.2.1/6.2.2题），分析时间复杂度和适用场景，为后续算法奠定基础。
图的遍历算法
- 深度优先搜索（DFS）与广度优先搜索（BFS）的代码实现（如6.3.1-6.3.3题），对比两种遍历策略的应用场景，并通过多道题目强化对连通性检测、路径查找等问题的解决能力。
图的应用算法
- 聚焦经典算法实践，涵盖最短路径（Dijkstra、Floyd）、最小生成树（Prim、Kruskal）、拓扑排序等（如6.4.1题），结合代码实现剖析算法思想，提升实际问题建模能力。
拓展与总结
- 通过链式存储结构示意图等思维扩展题（6.4.2题）深化对复杂图结构的理解，最后的归纳总结梳理图算法知识体系，强调从存储到应用的完整链路，助力读者构建系统化认知。
全文以“理论+代码”双主线展开，注重算法思想与工程实践的融合，适用于进阶学习与面试备考，为高效解决图相关复杂问题提供全面指导。

6.2数据结构与算法之图的存储及基本操作题目

6.2.1题：

代码算法实现思路：

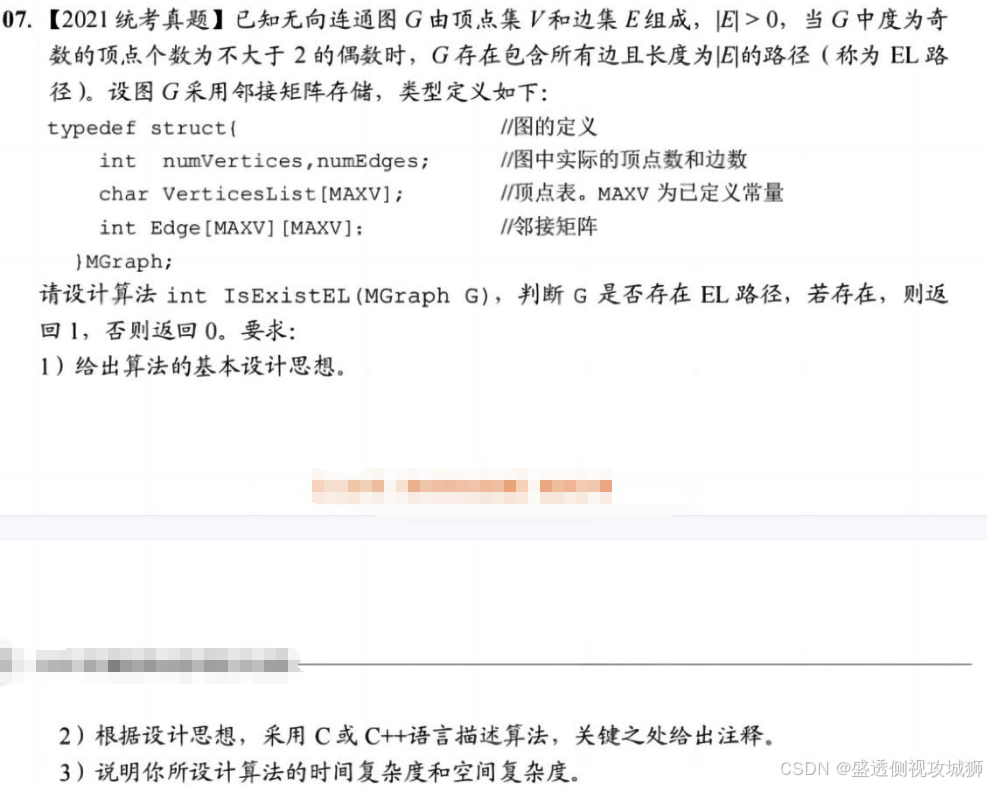
题干已经告诉我们算法的思想。
对于采用邻接矩阵存储的无向图，在邻接矩阵的每一行(列)中,非零元素的个数为本行(列)对应顶点的度。
可以依次计算连通图G中各顶点的度,并记录度为奇数的顶点个数,若个数为0或2,则返回1,否则返回0.

核心代码实现：

int IsExistEL(MGraph G) {  
    //采用邻接矩阵存储，判断图是否存在 EL 路径  
    int degree, i, j, count = 0;  
    for (i = 0; i < G.numVertices; i++) {  
        degree = 0;  
        for (j = 0; j < G.numVertices; j++)  
            degree += G.Edge[i][j];       //依次计算各个顶点的度  
        if (degree % 2 != 0)  
            count++;      //对度为奇数的顶点计数  
    }  
    if (count == 0 || count == 2)  
        return 1;               //存在 EL 路径，返回 1  
    else  
        return 0;               //不存在 EL 路径，返回 0  
}

6.2.2题：

代码算法实现思路：

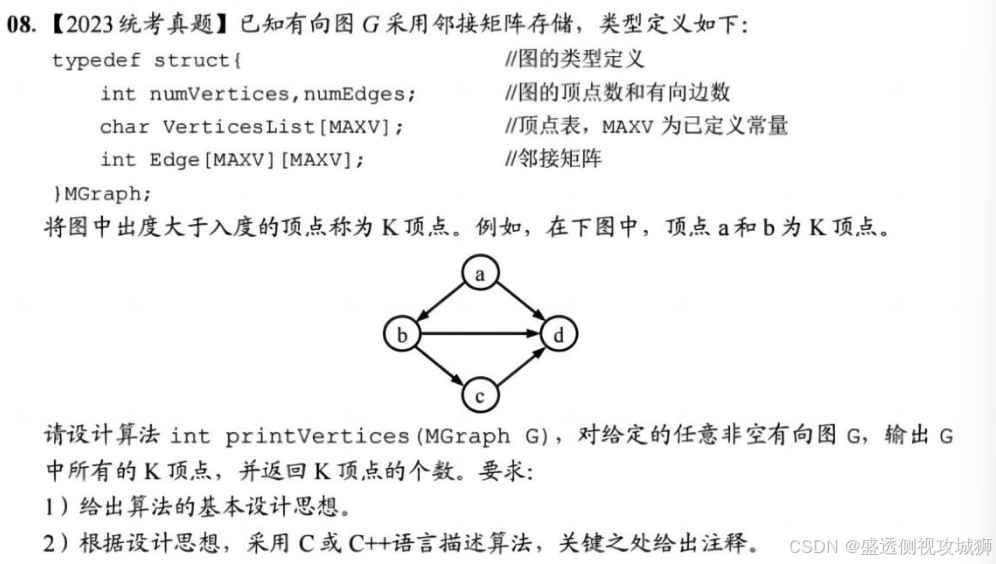
采用邻接矩阵表示有向图时,一行中1的个数为该行对应顶点的出度,一列中1的个数为该列对应顶点的入度。
使用一个初值为零的计数器记录K顶点的个数。
对图G的每个顶点,根据邻接矩阵计算其出度outdegree和入度indegree。
若outdegree-indegree>0,则输出该顶点且计数器加1。
最后返回计数器的值。

核心代码实现：

int printVertices (MGraph G) {  
//采用邻接矩阵存储，输出 K 顶点，返回个数  
    int indegree, outdegree, k, m, count=0;  
    for (k=0;k<G.numVertices;k++) {  
        indegree=outdegree=0;  
        for (m=0;m<G.numVertices;m++)     //计算顶点的出度  
            outdegree+=G.Edge [k][m];  
        for (m=0;m<G.numVertices;m++)     //计算顶点的入度  
            indegree+=G.Edge [m][k];  
        if (outdegree>indegree) {  
            printf("%c",G.VerticesList[k]);  
            count++;  
        }  
    }  
    return count;                               //返回 K 顶点的个数  
}

6.3数据结构与算法之图的遍历算法题目

6.3.1题

代码算法实现思路：

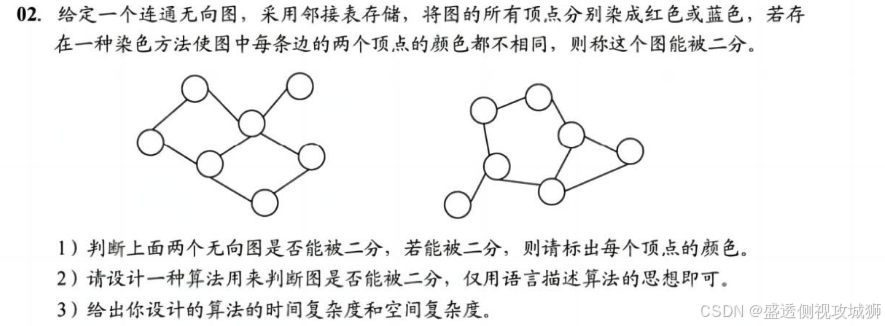
利用广度优先搜索（BFS）对图进行染色。
从每个未访问的顶点出发，将其染为一种颜色（如 0），然后遍历其邻接点，将邻接点染为相反颜色（如 1）。
若在遍历过程中发现邻接点颜色与当前顶点颜色相同，则图不能被二分。

核心代码实现：

#include <vector>
#include <queue>
using namespace std;

// 邻接表结构
struct ALNode {
    int adjvex;
    ALNode* next;
    ALNode(int v) : adjvex(v), next(nullptr) {}
};

struct ALGraph {
    vector<ALNode*> vertices;
    int numVertices;
    ALGraph(int n) : numVertices(n), vertices(n, nullptr) {}
};

bool isBipartite(ALGraph& G) {
    vector<int> color(G.numVertices, -1); // -1表示未染色，0和1表示两种颜色
    queue<int> q;

    for (int i = 0; i < G.numVertices; ++i) {
        if (color[i] == -1) { // 未访问过的顶点
            q.push(i);
            color[i] = 0; // 初始染色为0

            while (!q.empty()) {
                int u = q.front();
                q.pop();

                ALNode* p = G.vertices[u];
                while (p != nullptr) {
                    int v = p->adjvex;
                    if (color[v] == -1) { // 未染色，染成相反颜色
                        color[v] = color[u] ^ 1;
                        q.push(v);
                    } else if (color[v] == color[u]) { // 颜色冲突，非二分图
                        return false;
                    }
                    p = p->next;
                }
            }
        }
    }
    return true; // 所有顶点检查完毕，无冲突
}

6.3.2题

代码算法实现思路：

一个无向图 G 是一棵树的条件是：G 必须是无回路的连通图或有 n-1条边的连通图。
这里采用后者作为判断条件。
对连通的判定,可以用能否一次遍历全部顶点来实现。
可以采用深度优先搜索算法在遍历图的过程中统计可能访问到的顶点个数和边的条数,若一次遍历就能访问到n个顶点和n-1条边，则可断定此图是一棵树。

核心代码实现：

bool isTree (Graph& G) {  
    for (i=1;i<=G.vexnum;i++)  
        visited[i]=FALSE;          //访问标记 visited[]初始化  
    int Vnum=0,Enum=0;             //记录顶点数和边数  
    DFS (G,1,Vnum,Enum,visited);  
    if (Vnum==G.vexnum&&Enum==2*(G.vexnum-1))  
        return true;               //符合树的条件  
    else  
        return false;              //不符合树的条件  
}  
void DFS(Graph& G,int v,int& Vnum,int& Enum,int visited[]){  
//深度优先遍历图 G，统计访问过的顶点数和边数，通过 Vnum 和 Enum 返回  
    visited[v]=TRUE;Vnum++;       //作访问标记，顶点计数  
    int w=FirstNeighbor (G,v);    //取 v 的第一个邻接顶点  
    while (w!=-1) {               //当邻接顶点存在  
        Enum++;                    //边存在，边计数  
        if (!visited[w])           //当该邻接顶点未访问过  
            DFS (G,w,Vnum,Enum,visited);  
        w=NextNeighbor (G,v,w);  
    }  
}

6.3.3题

代码算法实现思路：

两个不同的遍历算法都采用从顶点v,出发,依次遍历图中每个顶点,直到搜索到顶点v
若能够搜索到v,则说明存在由顶点v到顶点v的路径。

DFS核心代码实现：

int visited[MAXSIZE] = {0};    //访问标记数组  
void DFS(ALGraph G, int i, int j, bool &can_reach) {  
    //深度优先判断有向图 G 中顶点 v_i 到顶点 v_j 是否有路径，用 can_reach 来标识  
    if (i == j) {  
        can_reach = true;  
        return;                //i 就是 j  
    }  
    visited[i] = 1;             //置访问标记  
    for (int p = FirstNeighbor(G, i); p >= 0; p = NextNeighbor(G, i, p))  
        if (!visited[p] && !can_reach)     //递归检测邻接点  
            DFS(G, p, j, can_reach);  
}

BFS核心代码实现：

int visited[MAXSIZE]={0};       //访问标记数组  
int BFS(ALGraph G, int i,int j){  
//广度优先判断有向图 G 中顶点 v_i到顶点 v_j是否有路径，是则返回 1，否则返回 0  
    InitQueue(Q); EnQueue(Q,i);  //顶点 i 入队  
    while(!isEmpty(Q)){          //非空循环  
        DeQueue(Q,i);            //队头顶点出队  
        visited[i]=1;            //置访问标记  
        if(i==j)  return 1;  
        for(int p=FirstNeighbor(G,i);p;p=NextNeighbor(G,i,p)){  
                               //检查所有邻接点  
            if(p==j)  
                return 1;       //若 p==j，则查找成功  
            if(!visited[p]){   //否则，顶点 p 入队  
                EnQueue(Q,p);  
                visited[p]=1;  
            }  
        }  
    }  
    return 0;  
}

补充：

本题也可以这样来做：调用以 i 为参数的 DFS（G，i）或 BFS（G，i）
执行结束后判断visited[j]是否为TRUE,若是则说明v已被遍历,图中必存在由v,到v,的路径。
但此种解法每次都耗费最坏时间复杂度对应的时间,需要遍历与v,连通的所有顶点。

6.3.4题

代码算法实现思路：

可以采用基于递归的深度优先遍历算法,从结点u出发,递归深度优先遍历图中结点,若访问到结点v,则输出该搜索路径上的结点。
综上所述,设置一个path数组来存放路径上的结点(初始为空)，d 表示路径长度（初始为-1）。
查找从顶点 u 到 v 的简单路径过程说明如下（我们可以假设查找函数名为 FindPath())

核心代码实现：

void FindPath(AGraph *G,int u,int v,int path[],int d){  
    int w;  
    ArcNode *p;  
    d++;                                  //路径长度增1  
    path[d]=u;                            //将当前顶点添加到路径中  
    visited[u]=1;                         //置已访问标记  
    if(u==v)                              //找到一条路径则输出  
        print(path[]);                    //输出路径上的结点  
    p=G->adjlist[u].firstarc;   //p指向u的第一个相邻点  
    while(p!=NULL){  
        w=p->adjvex;                      //若顶点w未访问，递归访问它  
        if(visited[w]==0)  
            FindPath(G,w,v,path,d);  
        p=p->nextarc;                     //p指向u的下一个相邻点  
    }  
    visited[u]=0;                         //恢复环境，使该顶点可重新使用  
}

6.4数据结构与算法之图的应用算法题

6.4.1题

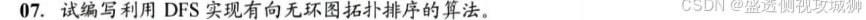
代码算法实现思路：

之前给出了DFS实现拓扑排序的思想
那么我们可以利用DFS求各顶点结束时间的代码(在DFS的基础上加入了time变量)。
将结束时间从大到小排序,即可得到拓扑序列。

核心代码实现：

void FindPath(AGraph *G,int u,int v,int path[],int d){  
    int w;  
    ArcNode *p;  
    d++;                                  //路径长度增1  
    path[d]=u;                            //将当前顶点添加到路径中  
    visited[u]=1;                         //置已访问标记  
    if(u==v)                              //找到一条路径则输出  
        print(path[]);                    //输出路径上的结点  
    p=G->adjlist[u].firstarc;   //p指向u的第一个相邻点  
    while(p!=NULL){  
        w=p->adjvex;                      //若顶点w未访问，递归访问它  
        if(visited[w]==0)  
            FindPath(G,w,v,path,d);  
        p=p->nextarc;                     //p指向u的下一个相邻点  
    }  
    visited[u]=0;                         //恢复环境，使该顶点可重新使用  
}  

bool visited[MAX_VERTEX_NUM];         //访问标记数组  
void DFSTraverse(Graph G){  
    for(v=0;v<G.vexnum;++v)  
        visited[v]=FALSE;               //初始化访问标记数组  
    time=0;  
    for(v=0;v<G.vexnum;++v)            //本代码从v=0开始遍历  
        if(!visited[v]) DFS(G,v);  
}  
void DFS(Graph G,int v){  
    visited[v]=TRUE;  
    visit(v);  
    for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))  
        if(!visited[w]){               //w为v的尚未访问的邻接点  
            DFS(G,w);  
        }  
    time=time+1;finishTime[v]=time;  
}

6.4.2思维扩展题

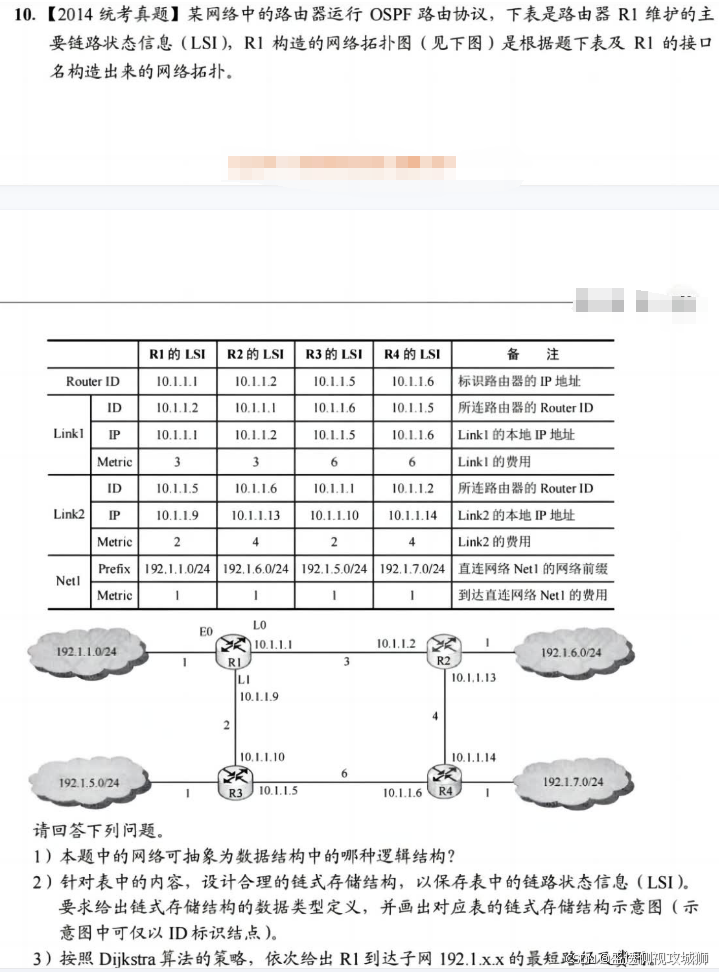
解题思路：

看起来感觉难度较大，但仔细分析就可发现考查的其实是邻接表的数据结构。
1）图题中给出的是一个简单的网络拓扑图，可以抽象为无向图。
2)图的常用存储结构有邻接矩阵法和邻接表法,其中邻接表法属于链式存储结构,因此本题的基本思路就是写出邻接表的数据类型定义，并根据题意调整相应的边表结点和顶点表结点的成员变量。
- 具体分析如下：邻接表由表头顶点和弧顶点组成。
- 根据题目给出的图和表，可将顶点分为三类：路由器、网络和链路。
  - 路由器是连接网络和链路的载体，因此可将它作为表头顶点。
  - 网络和链路则是连接路由器的边,因此可将它们作为弧顶点。
  - 为了简化代码,可将网络和链路的结构合并为一个,用一个标志位来区分它们,这样就可用邻接表来实现图的存储。
链式存储结构的如下图所示。

其数据类型代码定义实现：

typedef struct{  
unsigned int ID, IP;  
}LinkNode;                //Link 的结构  
typedef struct{  
unsigned int Prefix, Mask;  
}NetNode;                 //Net 的结构  
typedef struct Node{  
int Flag;                 //Flag=1 为 Link;Flag=2 为 Net  
union{  
    LinkNode Lnode;  
    NetNode Nnode  
}LinkORNet;  
Unsigned int Metric;  
struct Node *next;  
}ArcNode;                  //弧结点  
typedef struct hNode{  
unsigned int RouterID;  
ArcNode *LN_link;  
struct hNode *next;  
}HNODE;                    //表头结点

其对应表的链式存储结构示意图

深入浅出之图算法归纳总结🌟🌟🌟

图的很多程序对采用邻接表或邻接矩阵的存储结构都适用
主要原因是在图的基本操作函数中保持了相同的参数和返回值，而封闭了内部实现细节。

//例如，取 x 邻接顶点 y 的下一个邻接顶点的函数 NextNeighbor (G, x, y)。  

//1）用邻接矩阵作为存储结构  
int NextNeighbor (MGraph& G, int x, int y) {  
    if (x != -1 && y != -1) {  
        for (int col = y + 1; col < G.vexnum; col++)  
            if (G.Edge[x][col] > 0 && G.Edge[x][col] < maxWeight)  
                return col;                //maxWeight 代表∞  
    }  
    return -1;  
}  


//2）用邻接表作为存储结构  
int NextNeighbor (ALGraph& G, int x, int y) {  
    if (x != -1) {  
        ArcNode *p = G.vertices[x].first;    //顶点 x 存在，对应边链表第一个边结点  
        while (p != NULL && p->data != y)    //寻找邻接顶点 y  
            p = p->next;  
        if (p != NULL && p->next != NULL)  
            return p->next->data;             //返回下一个邻接顶点  
    }  
    return -1;  
}

本文参与腾讯云自媒体同步曝光计划，分享自作者个人站点/博客。

原始发表：2025-03-23，如有侵权请联系 cloudcommunity@tencent.com 删除

可视化