【数据结构】邻接表 vs 邻接矩阵：5大核心优势解析与稀疏图存储优化指南

导读

大家好，很高兴又和大家见面啦！！！

图作为一种复杂的数据结构，其高效存储与操作一直是算法设计的核心问题。邻接矩阵虽能快速判断顶点间关系，但在稀疏图中却面临空间浪费严重的瓶颈。为此，邻接表（Adjacency List）应运而生——它通过为每个顶点维护邻居链表，以空间复杂度 (O(V+E)) 的灵活结构，成为稀疏图、动态图及大规模图场景下的理想选择。

本文从邻接矩阵的不足切入，逐步剖析邻接表的设计思想、存储结构（顶点表与边表）与代码实现（C语言示例），并通过时间复杂度、空间复杂度对比，揭示其性能优势。同时，深入解读邻接表的五大核心特点：

1. 如何高效遍历邻居？
2. 为何判断边存在性效率较低？
3. 有向图与无向图在入度、出度计算上的差异；
4. 邻接表为何不具备唯一性？
5. 稀疏图场景下为何更优？

无论您是初学图论，还是需优化图算法效率，本文将为理解邻接表提供清晰的路径，助您在工程实践中精准选择数据结构，平衡时空效率。

一、邻接矩阵的不足

在邻接矩阵法中，我们通过一维数组存储图中的顶点信息，二维数组存储图中的边的信息。

对于稠密图这种边的数量较多的图而言，邻接矩阵是一个非常实用的存储结构。

通过空间换时间的操作，能够快速的找到两个顶点之间是否存在将其连通的边或者弧。

但是因为邻接矩阵中不仅记录了已有边的信息，还记录了不存在的边的信息，这就导致我们在计算图中边的总数时，会花费大量的时间。

在这种情况下，像稀疏图这种边的数量很少的图，通过邻接矩阵进行存储边的信息，就不是那么的合适。

为了优化邻接矩阵中对空间浪费的问题，我们可以采用链表的方式来存储图中的边，以达到减少空间的损耗。

通过一维数组存储顶点信息，链表存储边的信息共有3中存储结构：

• 邻接表法
• 十字链表
• 邻接多重表

接下来我们就来认识以下第一种存储结构——邻接表法（Adjacency List Method）。

二、邻接表

所谓的邻接表，是指对图 G 中的每个顶点 v_i 都建立一个单链表，第 i 个链表中的结点表示依附于顶点 v_i 的边（对于有向图则是以顶点 v_i 为弧尾的弧），这个单链表就称为顶点的边表 （对于有向图则称为出边表）。边表的头指针和顶点的数据信息采用顺序存储，称为顶点表。

在邻接表中存在两种结点：

• 顶点表结点：
  • 顶点域：存储顶点信息
  • 边表头指针：指向第一条边的边表结点
• 边表结点：
  • 邻接点域：存储与头结点邻接顶点的顶点编号
  • 指针域：指向下一条边的边表结点

邻接表.jpg

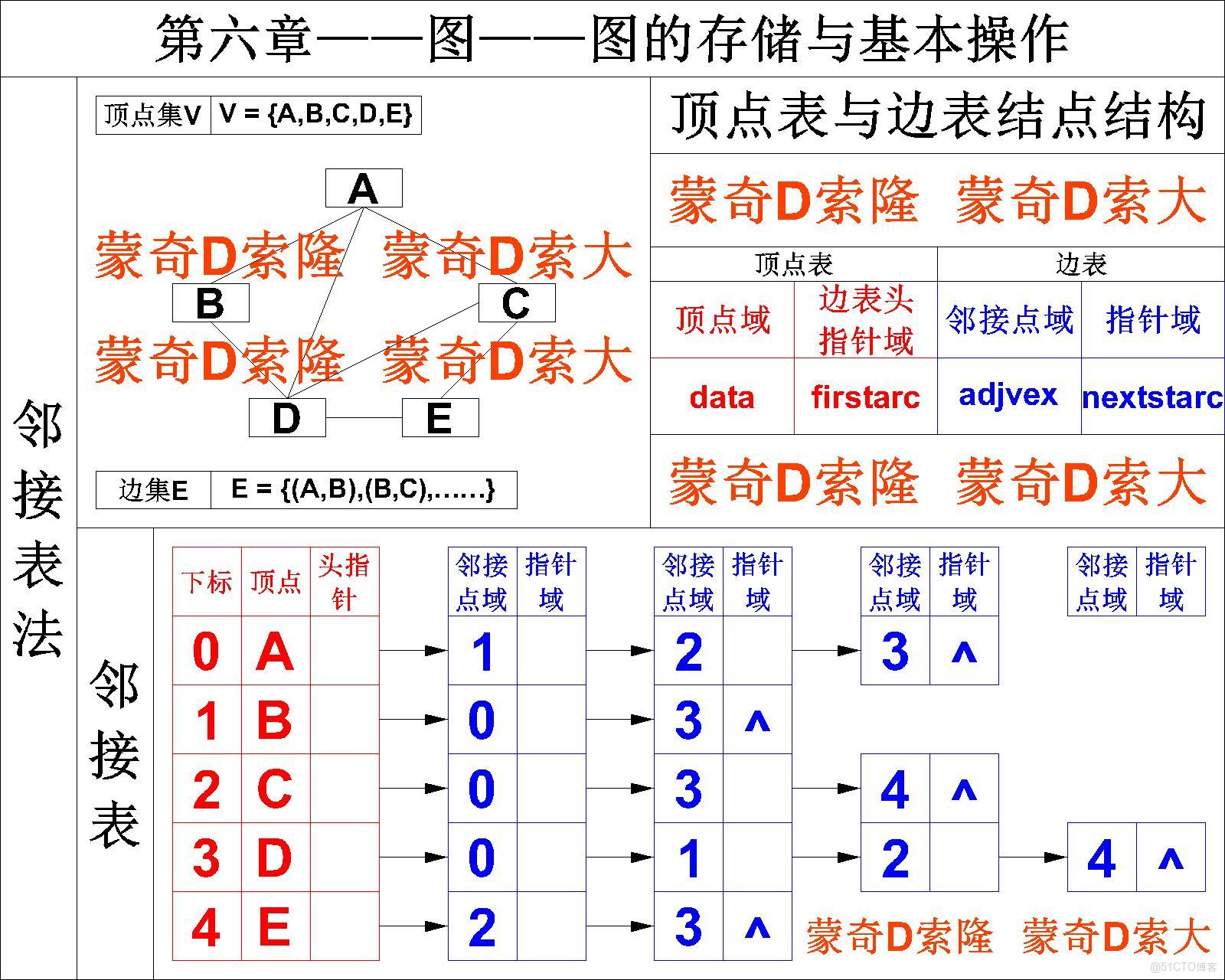
在邻接表中，每个顶点所对应的边表，都记录了与该顶点邻接的其它顶点的编号信息，我们通过该编号信息就能够从顶点表中找到该顶点的信息，从而获取当前边的信息。

就比如，上图中存储的是无向图，顶点A的第一个边表结点中邻接点域存放的编号为1，那么，我们通过查询顶点表中的编号即可得到该顶点为B，因此我们就得到了依附于顶点 A, B 的边 (A, B) ；

当存储的是有向图时，此时边表中记录的是弧尾顶点的编号信息，那么我们由该编号信息获取到该顶点信息时，这个顶点就是弧的弧尾。

graph LR
a--->b--->c
b--->a
0--->A[a/出边表头指针]--->B[1/指针域]--->B'[NULL]
1--->C[b/出边表头指针]--->D[0/指针域]--->D'[2/指针域]--->D''[NULL]
2--->E[c/出边表头指针]--->E'[NULL]

如上图所示，当我们从顶点a的出边表头指针找到第一个邻接的顶点编号信息时，我们再通过顶点表获取到了该顶点为 b，此时我们就得到了有向图的一条从a到b的弧 <a, b>

三、存储结构

在邻接表中，我们需要单独定义顶点表结点与边表（出边表）结点，对应的C语言存储结构如下所示：

typedef char VertexType;
typedef int AdjVexType;
#define MAXSIZE 5
//边表结点
typedef struct EdgeNode {
	AdjVexType adjvex;			// 邻接顶点编号
	struct EdgeNode* nextarc;	// 下一个边表结点
}EdgeNode;						// 边表结点
//顶点表结点
typedef struct VexNode {
	VertexType data;			// 顶点信息
	EdgeNode* firstarc;			// 边表头指针
}VexNode;						// 顶点表结点
//邻接表
typedef struct Adjacency_List_Method_Graph {
	VexNode vexlist[MAXSIZE];	// 顶点表
	int vexnum;					// 当前顶点数
	int edgenum;				// 当前边数
}ALGraph;						// 邻接表

四算法评价

4.1 时间复杂度

在邻接表中，我们在进行遍历时，实际上就是完成了一次顺序表的遍历以及每个顺序表所附带的链表的遍历，因此其时间复杂度是有顺序表的遍历与链表的遍历综合来看：

• 顺序表的遍历时间复杂度为 O(|V|) ，这里的 |V| 为顶点的数量
• 链表的遍历时间与边被记录的次数有关： 在无向图中，由于边会被记录两次，所以遍历时间复杂度为 O(|2E|) 在有向图中，边只会被记录一次，所以遍历时间复杂度为 O(|E|)

因此总的时间复杂度为 ：

• 无向图：T(N) = O(|V| + 2|E|);
• 有向图：T(N) = O(|V| + |E|);

4.2 空间复杂度

在邻接表中，我们需要为顶点和边分别申请空间：

• 顶点申请的空间数量由顶点个数决定，即空间复杂度为 O(|V|)
• 边申请的空间数量由边个数决定 在无向图中，每条边都需要被记录两次，因此对应的空间复杂度为 O(|2E|) 在有向图中，每条边只需要被记录一次，因此对应的空间复杂度为 O(|E|)

记录顶点与边数量的变量所占用的空间是固定的，其对应的空间复杂度为 O(1) ，在总的空间复杂度中可以忽略不计。

因此在无向图中总的空间复杂度为 T(N) = O(|V| + |2E|)；在有向图中总的空间复杂度为 T(N) = O(|V| + |2E|)

五、邻接表特点

图的邻接表存储具有以下特点：

1. 若G为无向图，则所需要的存储空间为 O(|V| + 2|E|) ；若为有向图，则所需的存储空间为 O(|V| + |E|).
2. 对于稀疏图（边数较少的图），采用邻接表表示将极大地节省存储空间
3. 在邻接表中，给定一个顶点，能很容易地找到它的所有邻边，因为只需要读取它的邻接表。在邻接矩阵中，相同的操作则需要扫描一行，花费的时间为 O(N) 。但是，若确定给定的两个顶点之间是否存在边，则在邻接矩阵中能快速查到，而在邻接表中则需要再相应顶点对应的边表中查找另一结点，效率极低。
4. 在无向图的邻接表中，求某个顶点的度秩序计算其邻接表中的边表结点个数。在有向图的邻接表中，求某个顶点的出度只需要计算其邻接表中的边表结点个数；但求某个顶点 x 的入度则需遍历全部的邻接表，统计邻接点域为 x 的边表结点个数。
5. 图的邻接表表示并不唯一，因为在每个顶点对应的边表中，各边结点的链接次序是任意的，它取决于建立邻接表的算法及边的输入次序。

5.1 特点解读

邻接表的特点的前两点都很好理解，这里我就不再赘述。下面我们重点要理解后面的三点：

特点3

在邻接表中，给定一个顶点，能很容易地找到它的所有邻边，因为只需要读取它的邻接表。

这个点可能有朋友不太理解，为什么我们是需要读取邻接表而不是读取边表？

这是因为邻接表是有顶点表和边表组成，而边表中记录的是邻接顶点的定点表编号，如果我们是统计给定顶点边的个数，那么只看该顶点的边表即可，但是我们要想找到所有的边，那么就需要借助边表找到邻接顶点的编号，再由顶点表读取顶点信息才行，因此我们是读取的整个邻接表，而不是单一的边表。

在邻接矩阵中，相同的操作则需要扫描一行，花费的时间为 O(N) 。

这个点可能有朋友会奇怪，在顶点表中，我们也是扫描的边表，按理来说应该花费的时间也是 O(N) 呀，这两者有什么区别吗？

这是因为邻接矩阵中不管两个顶点之间是否存在边，每一行它都是 N 个空间，但是在邻接表中，只记录了与该顶点邻接的顶点编号，这个数量一定不会超过 N ，在大多数情况下，这个数量一定是小于 N 的，因为我们使用邻接表存储时，肯定是用于存储的稀疏图。

但是，若确定给定的两个顶点之间是否存在边，则在邻接矩阵中能快速查到，而在邻接表中则需要再相应顶点对应的边表中查找另一结点，效率极低。

在邻接矩阵中，我们只要知道了两个顶点的信息，我们就能通过点 a_{ij} 的值来判断这两个点之间是否存在边，查找效率为 O(1)；

但是在邻接表中，不管是存储的有向图还是无向图，我们至少都要遍历一个顶点的边表，如果是有向图，最坏情况下，两个顶点的边表我们都需要遍历，因此查找的效率为 O(M)（M \leq N）

特点4

在无向图的邻接表中，求某个顶点的度只需计算其邻接表中的边表结点个数。

在无向图的邻接表中，边表的结点个数就是与该顶点邻接的顶点的个数，也就是该顶点的度数。

在有向图的邻接表中，求某个顶点的出度只需要计算其邻接表中的边表结点个数；

在有向图的邻接表中，出边表中记录的是以该顶点为边尾的顶点数量，即该顶点的出度数；

但求某个顶点 x 的入度则需遍历全部的邻接表，统计邻接点域为 x 的边表结点个数。

在有向图中，对于一个顶点的入度数，我们无法通过自身的边表获取，只能够通过其它顶点的边表获取。

• 如果在其它顶点中找到了存储该顶点的编号信息的出边表结点，那就说明该顶点存在一条入度；
• 若在其它顶点中未找到存储该顶点的编号信息的出边表结点，那就说明此时查找的顶点没有弧是指向该顶点的；

特点5

图的邻接表表示并不唯一，因为在每个顶点对应的边表中，各边结点的链接次序是任意的，它取决于建立邻接表的算法及边的输入次序。

这个特点我们需要理解什么是唯一，在邻接矩阵中，矩阵中的信息是无法改变的，即我不管如何存储边的信息，它所对应的邻接矩阵是唯一的，有变化的无非就是矩阵中存储的值的变化；

但是在邻接表中，顶点表是不会改变，边表则是会变的：

• 在输入的顶点顺序一致时，如果我们在存储边表信息时，采用头插法存储和尾插法存储所得到的边表是不一样的；
• 在存储算法一致时，我们先输入顶点 a 的编号再输入顶点 b的编号与先输入顶点 b 的编号再输入顶点 a 的编号，此时得到的边表也是不一样的

因此我们说邻接表的表示不是唯一的，这个不唯一性就体现在边表上；

结语

邻接表以“顶点表+边表”的链式结构，完美解决了邻接矩阵在稀疏图中的空间浪费问题，其核心优势可总结为以下几点：

1. 空间高效：存储复杂度仅 (O(V+E))，尤其适合边数较少的稀疏图；
2. 动态灵活：快速增删边，适应图结构频繁变化的场景；
3. 邻居遍历高效：直接访问边表，时间复杂度与顶点的实际度数相关，避免邻接矩阵的全行扫描；
4. 支持复杂操作：天然适配DFS、BFS、最短路径等需要频繁遍历邻居的算法。

然而，邻接表并非完美： • 边存在性判断效率低（需遍历链表）； • 有向图入度计算复杂度高（需遍历全表）； • 邻接表表示不唯一，依赖输入顺序和存储逻辑。

实际应用中，邻接表与邻接矩阵的取舍需基于图密度与操作需求：稀疏图优先邻接表，稠密图或频繁边查询场景倾向邻接矩阵。

理解邻接表的设计哲学——“按需存储，避免冗余”，将帮助开发者在算法优化与工程实践中找到时空效率的最佳平衡点。