文档建议反馈控制台
首页
学习
活动
专区
圈层
工具
MCP广场
文章/答案/技术大牛
发布
社区首页 >专栏 >浅谈 Manacher

浅谈 Manacher

原创
作者头像
Clare613
修改于 2025-07-24 10:58:36
修改于 2025-07-24 10:58:36
1901
举报
文章被收录于专栏：ManacherManacher

前言：

关于 Manacher，有很多说法。有人说是马拉车，有人说是 Man 拉车。不多说了，本期难度一般，现在开讲。

何为 Manacher：

Manacher 算法主要是处理字符串中关于回文串的问题的，它可以在 $\mathcal{O(n)}$ 的时间处理出以字符串中每一个字符为中心的回文串半径，由于将原字符串处理成两倍长度的新串，在每两个字符之间加入一个特定的特殊字符，因此原本长度为偶数的回文串就成了以中间特殊字符为中心的奇数长度的回文串了。\

Manacher 算法提供了一种巧妙的办法，将长度为奇数的回文串和长度为偶数的回文串一起考虑，具体做法是，在原字符串的每个相邻两个字符中间插入一个分隔符，同时在首尾也要添加一个分隔符，分隔符的要求是不在原串中出现，一般情况下可以用 # 号。

怎么用：

我们分成三步：\

第一步，在原字符串中插入井号，如下：\

第二步，对于新的字符串，我们进行求 $p_i$ 的值，$p_i$ 表示以 $i$ 为中心点，最大的回文半径。\

我们可以发现，真正的回文串长度为 $p_i-1$，而原本的回文串的回文半径就等于 $\lfloor\dfrac{p_i}{2}\rfloor$。\

第三步，如下：

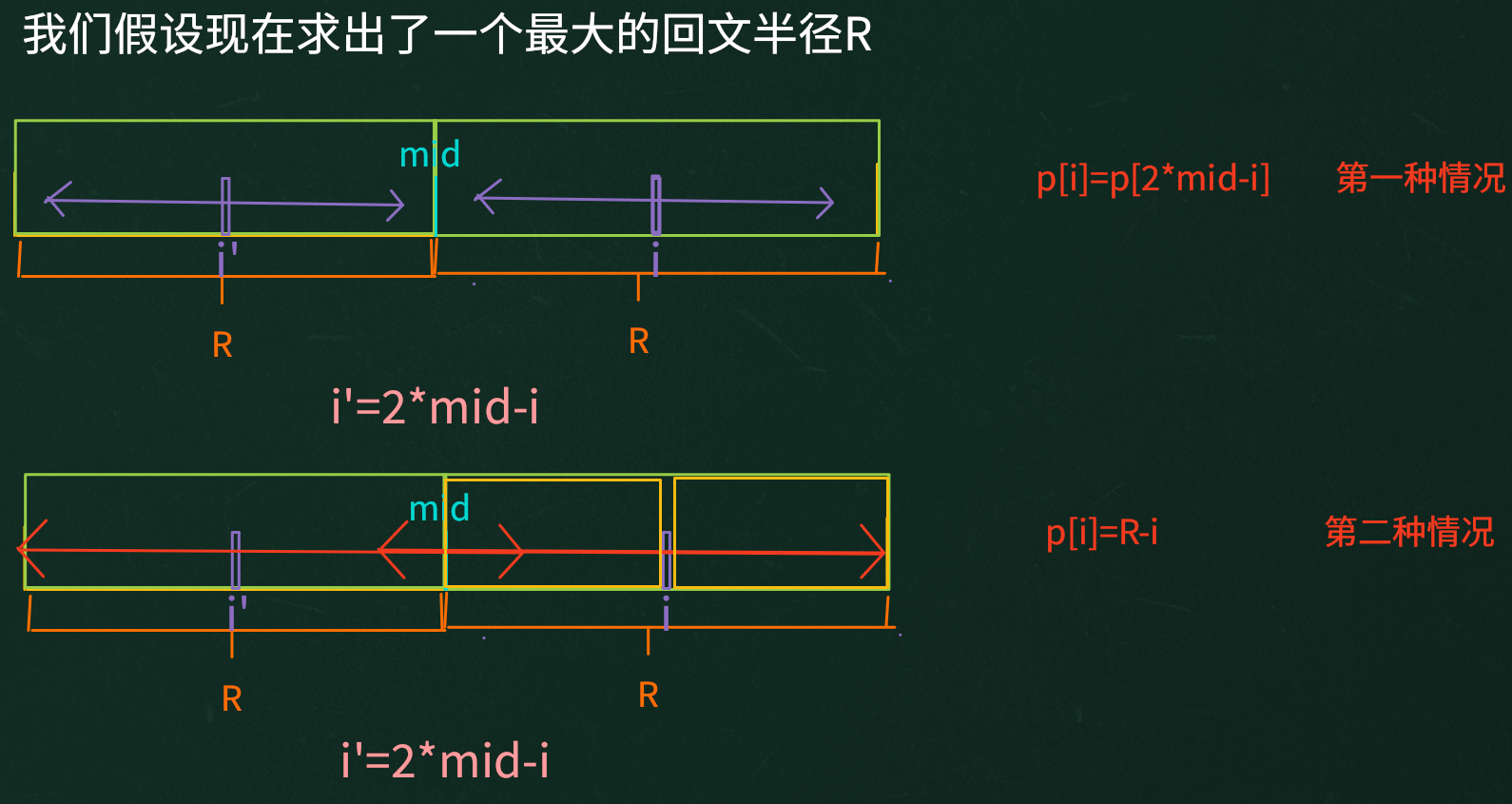
屏幕截图 2025-07-21 235235.png
屏幕截图 2025-07-21 235235.png

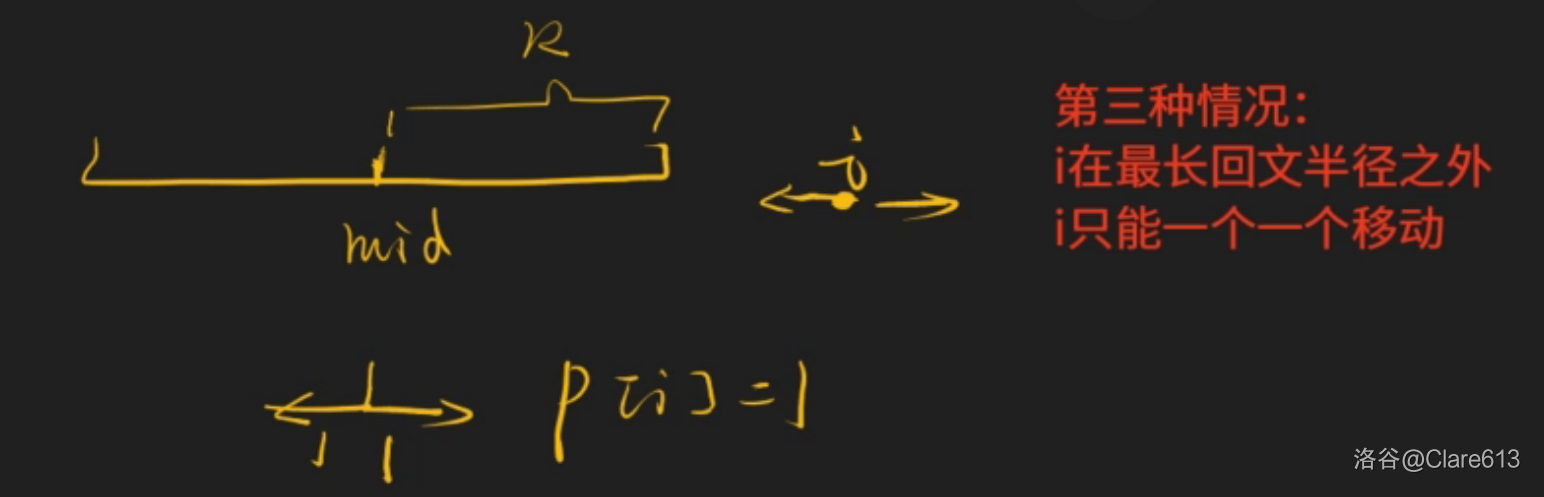
最终代码如下：

代码语言：cpp
复制
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s,str,w;
int n,m,p[110000005];
int k;
const int mod=998244353;
void add(){
	str=" ";
	int len=s.size();
	for(int i=0;i<s.size();i++){
		str+="#";
		str+=s[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
void manacher(){
	int r=0;
	int mid=0;
	int ans=0;
	for(int i=1;i<=m;i++){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while(str[i+p[i]]==str[i-p[i]]){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		ans=max(ans,p[i]-1);
	}
	cout<<ans;
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cout.tie(0)->sync_with_stdio(0);
	cin>>s;
	add();
	manacher();
	return 0;
}

例题：

本期题目是 5 蓝 1 紫，实际上是 4 蓝 2 紫，值得好好练习。

P3805 【模板】manacher：

模板题，直接写。

代码语言：cpp
复制
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s,str,w;
int n,m,p[110000005];
int k;
const int mod=998244353;
void add(){
	str=" ";
	int len=s.size();
	for(int i=0;i<s.size();i++){
		str+="#";
		str+=s[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
void manacher(){
	int r=0;
	int mid=0;
	int ans=0;
	for(int i=1;i<=m;i++){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while(str[i+p[i]]==str[i-p[i]]){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		ans=max(ans,p[i]-1);
	}
	cout<<ans;
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cout.tie(0)->sync_with_stdio(0);
	cin>>s;
	add();
	manacher();
	return 0;
}

P3501 POI 2010 ANT-Antisymmetry：

相对于模板题的判断部分有所改变，然后回文串的数量为 $\sum \dfrac{p_i}{2}$，其他的就没什么了。

代码语言：cpp
复制
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s,str;
int n,m,p[11000005];
void add(){
	str=" "+str;
	int len=s.size();
	for(int i=0;i<s.size();i++){
		str+="#";
		str+=s[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
void manacher(){
	int r=0;
	int mid=0;
	int ans=0;
	for(int i=1;i<=m;i+=2){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while((str[i+p[i]]+str[i-p[i]]=='1'+'0'||str[i+p[i]]+str[i-p[i]]=='#'+'#')){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		ans+=p[i]/2;
	}
	cout<<ans;
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cout.tie(0)->sync_with_stdio(0);
	cin>>n;
	cin>>s;
	add();
	manacher();
	return 0;
}

P1659 国家集训队 拉拉队排练：

这道题其实就是把所有的回文串的长度求出来，然后从大的开始逐步乘起来，假设有一个 $p_i=5$，那么可以产生 $5,3,1$ 这三种各一个，注意一定得是奇数。

代码语言：cpp
复制
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s,str;
int n,m,p[3000005],k;
int cnt[3000005];
const int MOD=19930726;
int poow(int a,int b){
	int cul=1;
	while(b){
		if(b%2) cul=cul*a%MOD;
		a=a*a;
		a%=MOD;
		b/=2;
	}
	return cul;
}
void add(){
	str=" "+str;
	int len=s.size();
	for(int i=0;i<s.size();i++){
		str+="#";
		str+=s[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
void manacher(){
	int r=0;
	int mid=0;
	int ans=1;
	for(int i=1;i<=m;i++){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while(str[i+p[i]]==str[i-p[i]]){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		cnt[p[i]-1]++;
	}
	for(int i=n;i>=1;i--){
		if(i%2==0) continue;
		if(k>=cnt[i]){
			ans*=poow(i,cnt[i]);
			ans%=MOD;
			k-=cnt[i];
		}
		else{
			if(k>0) ans*=poow(i,k);
			ans%=MOD;
			k=0;
			break;
		}
		cnt[i-2]+=cnt[i];
	}
	if(k!=0) cout<<-1;
	else cout<<ans;
}
signed main(){
//	freopen("y.in","r",stdin);
	cin>>n>>k;
	cin>>s;
	add();
	manacher();
	return 0;
}

P4555 国家集训队 最长双回文串&P4287 SHOI2011 双倍回文：

这两道题放一起讲，其实就是对于一个回文串的两侧的中心点为中心的回文串长度，大于等于这一侧的长度。

P4555 国家集训队 最长双回文串：
代码语言：cpp
复制
#include<bits/stdc++.h>
using namespace std;
string s,str;
int n,m,p[1000005],L[1000005],R[1000005];
int f[1000005],id[1000005];
void add(){
	str=" "+str;
	int len=s.size();
	for(int i=0;i<s.size();i++){
		str+="#";
		str+=s[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
void manacher(){
	memset(f,0x3f,sizeof(f));
	for(int i=1;i<=1000000;i++) id[i]=0;
	int r=0;
	int mid=0;
	int ans=0,last=0;
	for(int i=1;i<=m;i++){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while(str[i+p[i]]==str[i-p[i]]){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		L[i+p[i]-1]=max(L[i+p[i]-1],p[i]-1);
		R[i-p[i]+1]=max(R[i-p[i]+1],p[i]-1);
	}
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cout.tie(0)->sync_with_stdio(0);
	cin>>s;
	add();
	manacher();
	for(int i=3;i<=m;i+=2) R[i]=max(R[i],R[i-2]-2);
	for(int i=m-2;i>=1;i-=2) L[i]=max(L[i],L[i+2]-2);
	int ans=0;
	for(int i=1;i<=m;i+=2){
		if(R[i]&&L[i]) ans=max(ans,L[i]+R[i]);
	}
	cout<<ans;
	return 0;
}
P4287 SHOI2011 双倍回文：
代码语言：cpp
复制
#include<bits/stdc++.h>
#define int unsigned long long
using namespace std;
int n,m;
string x,str;
void add(){
	str="!";
	for(int i=0;i<n;i++){
		str+="#";
		str+=x[i];
	}
	str+="#";
	str+="@";
	m=n*2+1;
}
int p[50000005];
void manacher(){
	int r=0,mid=0;
	int ans=0;
	for(int i=1;i<=m;i++){
		p[i]=(i<r?min(p[mid*2-i],r-i+1):1);
		while(str[i-p[i]]==str[i+p[i]]){
			p[i]++;
			if(str[i]=='#'&&(p[i]-1)%4==0&&p[i-p[i]/2]>p[i]/2){
				ans=max(ans,p[i]-1);
			}
		}
		if(r<i+p[i]){
			r=i+p[i]-1;
			mid=i;
		}
	}
	cout<<ans<<"\n";
}
signed main(){
	cin>>n>>x;
	add();
	manacher();
	return 0;
}
/*
!#a#a#a#a#@ 
12345678901
*/

P11749 「TPOI-1C」Standard Problem.：

思路：

这题其实是道假题，我们可以发现如果字符串本身不是一个回文串，那么答案一定是 $0$。我们知道这个后就可以发现，从连着三个起，不管是连几个，他们的答案都是一样的。本质上就是首尾两个字符串，中间加个回文串。\

接着就是算公式，设一个为 $A$，两个为 $B$，三及以上为 $C$，可得：

$$(B-A)\times(k-1)+(C-2\times B+A)*\dfrac{(k-1)\times(k-2)}{2}+A$$

算后好对于答案取模输出即可。

code：
代码语言：cpp
复制
#include<bits/stdc++.h>
#define int long long
using namespace std;
string s,str,w;
int n,m,p[50000005];
int k;
const int mod=998244353;
void add(){
	str=" ";
	int len=w.size();
	for(int i=0;i<w.size();i++){
		str+="#";
		str+=w[i];
	}
	str+="#";
	str+="@";
	m=len*2+1;
}
int manacher(){
//	memset(p,0,sizeof(p));
	int r=0;
	int mid=0;
	int ans=0,last=0;
	for(int i=1;i<=m;i++){
		p[i]=((i<r)?min(p[2*mid-i],r-i):1);
		while(str[i+p[i]]==str[i-p[i]]){
			p[i]++;
		}
		if(i+p[i]>r){
			r=p[i]+i;
			mid=i;
		}
		ans+=p[i]/2;
		ans%=mod;
	}
	return ans;
}
signed main(){
	cin.tie(0)->sync_with_stdio(0);
	cout.tie(0)->sync_with_stdio(0);
	int T;
	cin>>T;
	while(T--){
		cin>>n>>k;
		cin>>s;
		w=s;
		add();
		int A=manacher();
		w=s+s;
		add();
		int B=manacher();
		w=s+s+s;
		add();
		int C=manacher();
		cout<<((((B-A+mod)%mod)*((k-1+mod)%mod))%mod+(C-2*B+A+mod*2)%mod*(((k-1)*(k-2)/2)%mod)+A)%mod<<"\n";
	}
	return 0;
}
/*
abaaba
*/

后话：

想要我更新更多算法的人回复 Clyyds 加上算法名，最后求大家点个赞吧。

原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。

如有侵权，请联系 cloudcommunity@tencent.com 删除。

c++11
c++14
c++17
c++20
c++

原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。

如有侵权，请联系 cloudcommunity@tencent.com 删除。

c++11
c++14
c++17
c++20
c++
评论
登录后参与评论
0 条评论
热度
最新
登录 后参与评论
推荐阅读
目录
  • 前言：
  • 何为 Manacher：
  • 怎么用：
  • 例题：
    • P3805 【模板】manacher：
    • P3501 POI 2010 ANT-Antisymmetry：
    • P1659 国家集训队 拉拉队排练：
    • P4555 国家集训队 最长双回文串&P4287 SHOI2011 双倍回文：
      • P4555 国家集训队 最长双回文串：
      • P4287 SHOI2011 双倍回文：
    • P11749 「TPOI-1C」Standard Problem.：
      • 思路：
      • code：
  • 后话：
领券

腾讯云开发者

扫码关注腾讯云开发者

扫码关注腾讯云开发者

领取腾讯云代金券

热门产品

热门推荐

更多推荐

Copyright © 2013 - 2025 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有 

深圳市腾讯计算机系统有限公司 ICP备案/许可证号：粤B2-20090059 深公网安备号 44030502008569

腾讯云计算（北京）有限责任公司 京ICP证150476号 |  京ICP备11018762号 | 京公网安备号11010802020287

问题归档专栏文章快讯文章归档关键词归档开发者手册归档开发者手册 Section 归档

Copyright © 2013 - 2025 Tencent Cloud.

All Rights Reserved. 腾讯云 版权所有

登录 后参与评论
1