经典算法回顾:全排列问题的递归与回溯解法
经典算法回顾:全排列问题的递归与回溯解法

深度解析算法之穷举vs暴搜vs深搜vs回溯vs剪枝
12.全排列
题目链接
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入: nums = [1,2,3] 输出: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1] ]
示例 2:
输入: nums = [0,1] 输出: [[0,1],[1,0] ]
示例 3:
输入: nums = [1] 输出: [[1] ]
提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
穷举-枚举->两层for循环
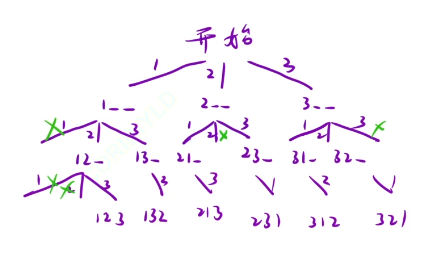
加上一个check数组实现剪枝 查看我们当前路径上哪些数字出现过
ret记录我们最终的结果 path记录我们深搜时候的路径
dfs函数 仅需关心,某个节点在干什么
细节问题: 回溯,将最后一个节点从path中删除,check的状态改成false 剪枝、 递归出口 遇到叶子节点直接添加结果
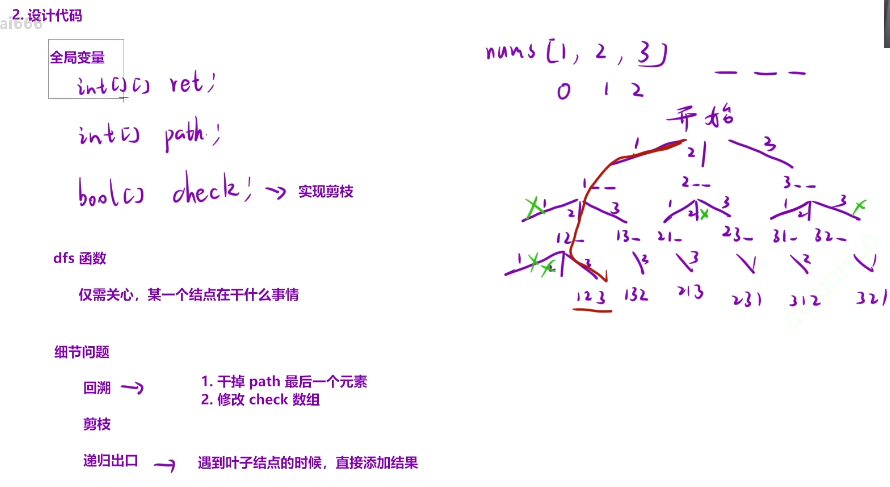
class Solution
{
vector<vector<int>>ret;//返回值
vector<int>path;//返回路径
bool check[7];//标记我们当前数字是否用过
public:
vector<vector<int>> permute(vector<int>& nums)
{
dfs(nums);
return ret;
}
void dfs(vector<int>& nums)
{
//递归出口
if(nums.size()==path.size())//说明我们到了叶子节点了,数组中的数都列举完了,我们再进行返回操作了
{
//将当前路径下的数据添加进ret之中,然后返回
ret.push_back(path);
return;//向上返回
}
for(int i=0;i<nums.size();i++)
{
if(check[i]==false)//说明此时的这个数还没有被用到
{
path.push_back(nums[i]);//将这个数加入到路径中去
check[i]=true;//改变这个数字的状态
dfs(nums);
//回溯->恢复现场,就是我们回来到当前节点后,我们将路径上的最后一个数据删掉并且改变状态就行了
path.pop_back();
check[i]=false;
}
}
//我们在每层返回后再将上一层添加进去的数据删除掉,这个就是剪枝操作
}
};就是将这个数组看成一棵树来进行问题的解决操作
先将递归出口写出,返回的条件就是此时的路径path数组中存的数字个数和nums中的一样,那么我们就可以判断此时就到了叶子节点了
然后我们再进行循环遍历我们的数组 如果此时我们的数的check值为false的话,那么就说明这个数还没用过,那么我们将这个数加入到我们的path中去,并且将这个数的check状态改变下,改变之后,我们就进行递归操作,看看这条路径下有多少个新的线路 递归调用回来之后,我们将路线path后面的那个数据删掉掉,并且将状态改变下,然后就这么一值进行循环操作
13.子集
题目链接
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入: nums = [1,2,3] 输出: [ [],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3] ]
示例 2:
输入: nums = [0] 输出: [[],[0] ]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
全局变量
dfs
细节问题:剪值、回溯、递归出口
某一个数选或者是不选,下面的就是我们的决策树
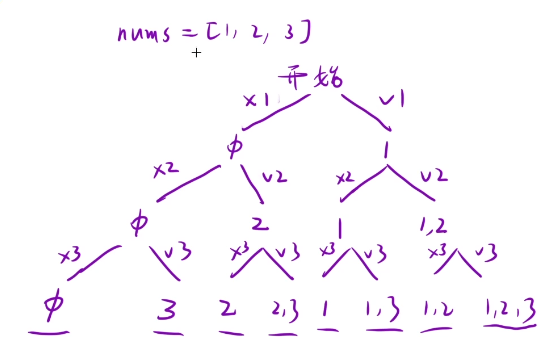
我们得用一个path数组来记录我们选或者不选
一个ret来进行结果的返回
当我们dfs递归回来的时候,我们需要将此时path数组中的最后一个元素给删除,这个就是回溯
当我们的此时i=nums.size()就说明我们到了递归出口了,那么我们就该进行返回操作了

解法二:每一个节点都是我们的结果,这种解法的话肯定是优于解法一的
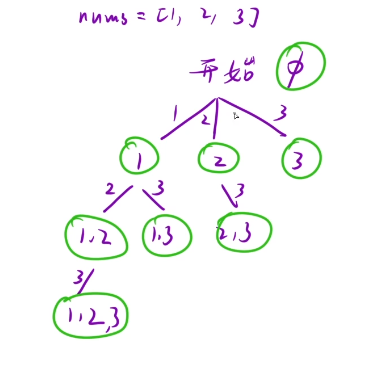
全局变量:int path [] int ret []

解法一的代码
class Solution
{
vector<vector<int>>ret;
vector<int>path;
public:
vector<vector<int>> subsets(vector<int>& nums)
{
//解法一:
dfs(nums,0);
return ret;
}
void dfs(vector<int>& nums,int pos)
{
if(pos==nums.size())//到了叶子节点的话,我们就到了递归出口了
{
ret.push_back(path);
return ;
}
//选
path.push_back(nums[pos]);//将这个pos位置的值算进去
dfs(nums,pos+1);
path.pop_back();//等我们递归结束后我们进行一个回溯的操作
//不选
dfs(nums,pos+1);//直接进入到下一层
}
};我们这里选或者不选 如果我们到了叶子节点的话我们就进行返回的操作,并且在返回之前将这个节点加入到path中去
若果没有到叶子节点的话,那么我们可以将pos这个位置加入到path中,并且从pos+1的位置开始进行递归调用 等我们调用完成了,我们回溯的时候将这个path中最后一个数据删除进行恢复的操作
然后如果不选的话我们直接地规避进入到下一层去
解法二的代码
class Solution
{
vector<vector<int>>ret;
vector<int>path;
public:
vector<vector<int>> subsets(vector<int>& nums)
{
//解法二:
dfs(nums,0);
return ret;
}
void dfs(vector<int>& nums,int pos)
{
//对于这种解法来说,每次进来都是一种结果
ret.push_back(path);//我们直接把path丢进去
for(int i=pos;i<nums.size();i++)
{
path.push_back(nums[i]);//我们直接将这个数丢到我们的path中去
dfs(nums,i+1);//我们直接进入到下一层去
path.pop_back();//递归回来的时候,我们将path中最后一个数删除了进行回溯恢复操作
}
}
};遍历过程:递归遍历 nums 数组,从 pos 到 nums.size() - 1,这样就避免了重复子集的生成,保证每个子集是唯一的。
- 深度优先搜索(DFS):每次递归时,都会选择一个数,加入当前路径
path,然后递归下去,直到所有的子集被生成出来。 - 回溯法:递归调用后,通过
pop_back来移除路径中的元素,恢复到上一层状态,继续尝试其他选择。 假设输入为nums = [1, 2, 3]:
- 初始
path = [],调用dfs([1, 2, 3], 0)。 - 第一次递归时,选择
1,路径变成[1],递归调用dfs([1, 2, 3], 1)。 - 第二次递归时,选择
2,路径变成[1, 2],递归调用dfs([1, 2, 3], 2)。 - 第三次递归时,选择
3,路径变成[1, 2, 3],递归调用dfs([1, 2, 3], 3)。 - 每次递归结束时,都会回溯到上一步,移除元素继续尝试其他选择。
最终返回的 ret 将是所有子集的集合,包括空集和整个集合: [ [], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3] ]。
这个循环从pos位置开始,这个很关键

