浅谈 tarjan
原创
前言：
今天讲一下 tarjan，大家加油，一举攻破它。
何为 tarjan：
如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。\
言简意赅。
做法：
看了这言简意赅得介绍，其实就可以想到 DFS 了。不得不说，长得确实有几分相似。先给代码：
void tarjan(int u){
low[u]=dfn[u]=++ti;
vis[u]=1;
st.push(u);
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
++scc;
while(!st.empty()){
int t=st.top();
op[scc].push\_back(t);
vis[t]=0;
color[t]=scc;
if(u==t){
st.pop();
break;
}
st.pop();
}
}
}看上去确实有点像 DFS，有人就会问了：放一个 stack 干什么？$dfn,low,vis,color,scc$ 又是干什么的？我们慢慢讲。\
强连通的定义：在一个**有向**图中，每两个点都可以相互到达，如下图：\
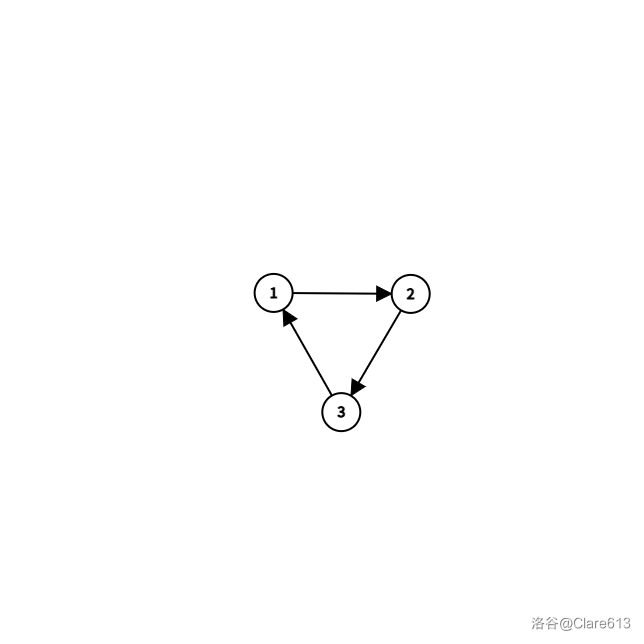
弱连通的定义：在一个**有向**图中，每两个点不一定都可以相互到达，但转为无向图后两个点都可以相互到达，如下图：\
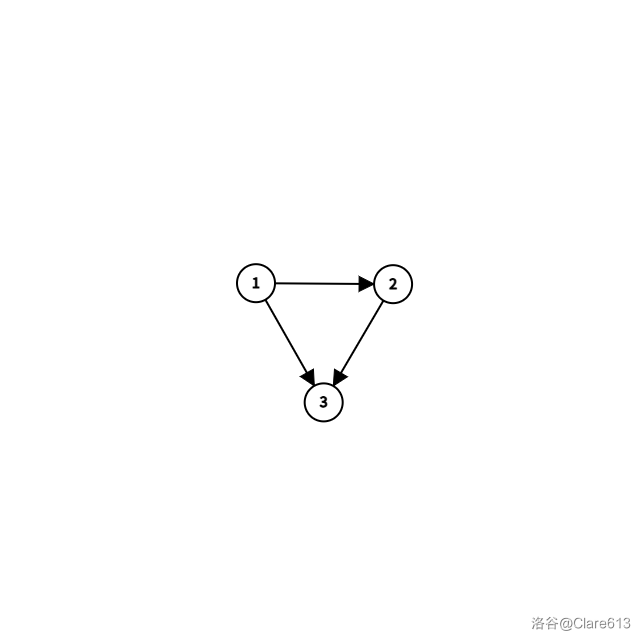
前面的介绍讲了 tarjan 是用来求强连通分量的。我们可以发现，如果要求前连通分量，我们可以想象这张图像一条链一样，然后有个别几条边是往回跳的，那么就需要记录可以跳到的最远的点，编号（时间戳）即为 $dfn$，low 即为最远编号。如图：\
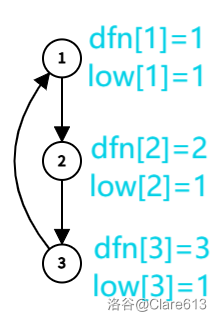
求出前连通分量后，我们可以记录下来，于是就有 $scc$（用于计数）、$color$（用于记录组别）、$st$（记录来的编号）、$vis$（记录是否在栈内）。
例题：
本期一共 18 题，这里挑个几道来讲。
B3609 图论与代数结构 701 强连通分量：
模板题，直接切去吧。
#include<bits/stdc++.h>
using namespace std;
int ti,scc,low[100005],dfn[100005],vis[100005],color[100005];
bool f[100005];
vector<int> g[100005],op[100005];
stack<int> st;
void tarjan(int u){
low[u]=dfn[u]=++ti;
vis[u]=1;
st.push(u);
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]){
++scc;
while(!st.empty()){
int t=st.top();
op[scc].push\_back(t);
vis[t]=0;
color[t]=scc;
if(u==t){
st.pop();
break;
}
st.pop();
}
}
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
g[u].push\_back(v);
}
for(int i=1;i<=n;i++){
if(color[i]==0) tarjan(i);
}
cout<<scc<<"\n";
for(int i=1;i<=n;i++){
if(!f[color[i]]){
f[color[i]]=1;
sort(op[color[i]].begin(),op[color[i]].end());
for(int j=0;j<op[color[i]].size();j++){
cout<<op[color[i]][j]<<" \n"[j==op[color[i]].size()-1];
}
}
}
return 0;
}P2661 NOIP 2015 提高组 信息传递：
对于所有的强连通分量的点数求 $\min$ 就切了。
#include<bits/stdc++.h>
using namespace std;
int scc,ti,dfn[1000005],low[1000005],vis[1000005],color[1000005];
vector<int> g[1000005],op[1000005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
color[st.top()]=scc;
vis[st.top()]=0;
op[scc].push\_back(st.top());
if(u==st.top()){
st.pop();
break;
}
st.pop();
}
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int u;
cin>>u;
g[i].push\_back(u);
}
for(int i=1;i<=n;i++){
if(color[i]==0)tarjan(i);
}
int minn=1e9;
for(int i=1;i<=n;i++){
if(op[color[i]].size()>1){
minn=min(minn,int(op[color[i]].size()));
}
}
cout<<minn;
return 0;
}P3387 【模板】缩点：
我们可以发现，每一个强连通分量都可以看作一个点，于是就有了缩点，按照缩点来求值即可。
#include<bits/stdc++.h>
using namespace std;
int vis[100005],low[100005],dfn[100005],s[100005],sum[100005],dp[100005],color[100005],ti,scc;
vector<int> g[100005],op[100005],eg[100005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
int t=st.top();
color[t]=scc;
vis[t]=0;
sum[scc]+=s[t];
op[scc].push\_back(t);
if(u==t){
st.pop();
break;
}
st.pop();
}
}
}
void dfs(int u){
dp[u]=sum[u];
int maxn=0;
for(int i=0;i<eg[u].size();i++){
int v=eg[u][i];
if(dp[v]==-1){
dfs(v);
}
maxn=max(maxn,dp[v]);
}
dp[u]+=maxn;
}
int u[100005],v[100005];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>s[i];
}
for(int i=1;i<=m;i++){
cin>>u[i]>>v[i];
g[u[i]].push\_back(v[i]);
}
for(int i=1;i<=n;i++){
if(color[i]==0) tarjan(i);
}
for(int i=1;i<=m;i++){
if(color[u[i]]!=color[v[i]]){
eg[color[u[i]]].push\_back(color[v[i]]);
}
}
memset(dp,-1,sizeof dp);
int ans=0;
for(int i=1;i<=scc;i++){
if(dp[i]==-1){
dfs(i);
ans=max(ans,dp[i]);
}
}
cout<<ans;
return 0;
}P2863 USACO06JAN The Cow Prom S：
题面十分直白，没有可以说的。
#include<bits/stdc++.h>
using namespace std;
int scc,ti,dfn[100005],low[100005],vis[100005],s[100005],color[100005],dp[100005],sum[100005];
vector<int> g[100005],eg[100005],op[100005];
bool f[100005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
color[st.top()]=scc;
sum[scc]+=s[st.top()];
vis[st.top()]=0;
op[scc].push\_back(st.top());
if(u==st.top()){
st.pop();
break;
}
st.pop();
}
}
}
void dfs(int u){
dp[u]=sum[u];
int maxn=0;
for(int i=0;i<eg[u].size();i++){
int v=eg[u][i];
if(dp[v]==-1){
dfs(v);
}
maxn=max(maxn,dp[v]);
}
dp[u]+=maxn;
}
int u[100005],v[100005];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>u[i]>>v[i];
g[u[i]].push\_back(v[i]);
}
for(int i=1;i<=n;i++){
if(color[i]==0)tarjan(i);
}
int ans=0;
for(int i=1;i<=scc;i++){
if(op[i].size()>1) ans++;
}
cout<<ans;
return 0;
}P2746 USACO5.3 校园网Network of Schools&P2812 校园网络【USACONetwork of Schools加强版】：
双倍经验，可以分为两个子任务：
- 找出度为 $0$ 的缩点个数。
- 找出入度为 $0$ 的缩点的个数，然后比较最大值。
很快就可以切掉。
#include<bits/stdc++.h>
using namespace std;
int scc,ti,dfn[1000005],low[1000005],vis[1000005],s[1000005],color[1000005],dp[1000005],sum[1000005];
vector<int> g[1000005],eg[1000005],op[1000005];
bool f[1000005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
color[st.top()]=scc;
sum[scc]+=s[st.top()];
vis[st.top()]=0;
op[scc].push\_back(st.top());
if(u==st.top()){
st.pop();
break;
}
st.pop();
}
}
}
int ans=0;
void dfs(int u){
dp[u]=sum[u];
for(int i=0;i<eg[u].size();i++){
int v=eg[u][i];
if(f[v]==0){
f[v]=1;
ans++;
}
if(dp[v]==-1) dfs(v);
}
}
int u[1000005],v[1000005],cnt1=0,cnt2=0;
bool fi1[1000005],fi2[1000005];
int main(){
int n,m=0;
cin>>n;
cnt2=n;
for(int i=1;i<=n;i++){
int s;
bool flag=0;
while(cin>>s){
if(s==0) break;
u[++m]=i;
v[m]=s;
g[i].push\_back(s);
}
}
for(int i=1;i<=n;i++){
if(color[i]==0)tarjan(i);
}
cnt1=cnt2=scc;
for(int i=1;i<=m;i++){
if(color[u[i]]!=color[v[i]]){
if(fi1[color[u[i]]]==0){
cnt1--;
fi1[color[u[i]]]=1;
}
if(fi2[color[v[i]]]==0){
cnt2--;
fi2[color[v[i]]]=1;
}
eg[color[u[i]]].push\_back(color[v[i]]);
}
}
memset(dp,-1,sizeof dp);
for(int i=1;i<=scc;i++){
if(dp[i]==-1){
dfs(i);
}
}
cout<<scc-ans<<"\n"<<(scc==1?0:max(cnt1,cnt2));
return 0;
}P5145 漂浮的鸭子：
求最长强连通距离。
#include<bits/stdc++.h>
using namespace std;
int scc,ti,dfn[1000005],low[1000005],vis[1000005],color[1000005],s[1000005],sum[1000005];
vector<int> g[1000005],op[1000005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
color[st.top()]=scc;
vis[st.top()]=0;
sum[scc]+=s[st.top()];
if(u==st.top()){
st.pop();
break;
}
st.pop();
}
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
int u;
cin>>u>>s[i];
g[i].push\_back(u);
}
for(int i=1;i<=n;i++){
if(color[i]==0)tarjan(i);
}
int maxn=0;
for(int i=1;i<=scc;i++){
maxn=max(maxn,sum[i]);
}
cout<<maxn;
return 0;
}UVA12167 Proving Equivalences：
找出入度为 $0$ 的缩点的个数，然后比较最大值。
#include<bits/stdc++.h>
using namespace std;
int scc,ti,dfn[100005],low[100005],vis[100005],color[100005];
vector<int> g[100005];
bool f[100005];
stack<int> st;
void tarjan(int u){
st.push(u);
vis[u]=1;
dfn[u]=low[u]=++ti;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[v],low[u]);
}
else if(vis[v]==1){
low[u]=min(low[u],dfn[v]);
}
}
if(dfn[u]==low[u]){
++scc;
while(!st.empty()){
color[st.top()]=scc;
vis[st.top()]=0;
if(u==st.top()){
st.pop();
break;
}
st.pop();
}
}
}
int u[100005],v[100005],cnt1=0,cnt2=0;
bool fi1[100005],fi2[100005];
int main(){
int T;
cin>>T;
while(T--){
memset(dfn,0,sizeof dfn);
memset(low,0,sizeof low);
memset(vis,0,sizeof vis);
memset(color,0,sizeof color);
memset(fi1,0,sizeof fi2);
memset(fi2,0,sizeof fi1);
ti=scc=0;
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) g[i].clear();
cnt2=n;
for(int i=1;i<=m;i++){
cin>>u[i]>>v[i];
g[u[i]].push\_back(v[i]);
}
for(int i=1;i<=n;i++){
if(color[i]==0)tarjan(i);
}
cnt1=cnt2=scc;
for(int i=1;i<=m;i++){
if(color[u[i]]!=color[v[i]]){
if(fi1[color[u[i]]]==0){
cnt1--;
fi1[color[u[i]]]=1;
}
if(fi2[color[v[i]]]==0){
cnt2--;
fi2[color[v[i]]]=1;
}
}
}
cout<<(scc==1?0:max(cnt1,cnt2))<<"\n";
}
return 0;
}P3388 【模板】割点（割顶）：
分三种情况：
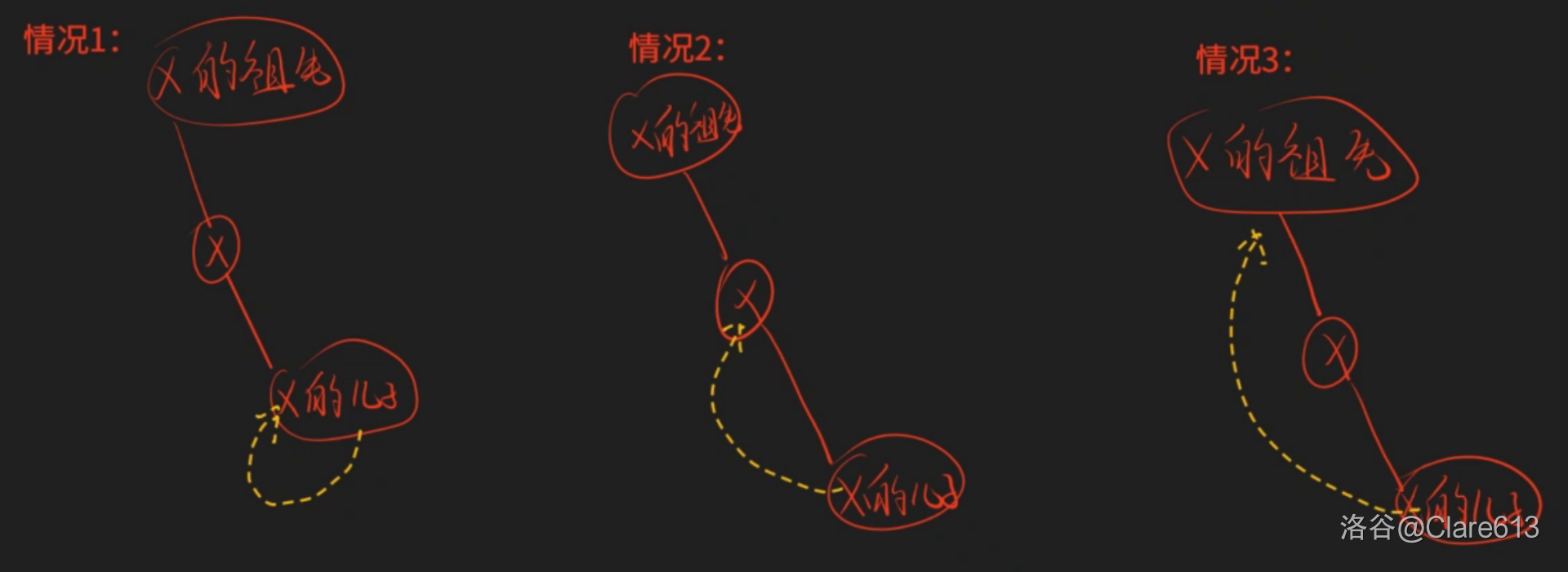
可得：当 $u\not=root||cnt\ge2$ 时，$u$ 为割点。
最终：
#include<bits/stdc++.h>
using namespace std;
int ti,scc,low[100005],dfn[100005],cut[100005],ans,root;
vector<int> g[100005],op[100005];
void tarjan(int u){
low[u]=dfn[u]=++ti;
int cnt=0;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(dfn[u]<=low[v]){
cnt++;
if(u!=root||cnt>=2){
cut[u]=1;
}
}
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
g[u].push\_back(v);
g[v].push\_back(u);
}
for(int i=1;i<=n;i++){
if(dfn[i]==0){
root=i;
tarjan(i);
}
}
for(int i=1;i<=n;i++){
if(cut[i]) ans++;
}
cout<<ans<<"\n";
for(int i=1;i<=n;i++){
if(cut[i]) cout<<i<<" ";
}
return 0;
}U132350 【模板】割边（桥）：
还是分三种情况：
可得：当 $dfnu<lowv$ 时，$u$ 为割边。
最终：
#include<bits/stdc++.h>
using namespace std;
int ti,scc,low[100005],dfn[100005],cut[100005],ans,root;
vector<int> g[100005],op[100005];
void tarjan(int u,int fa){
low[u]=dfn[u]=++ti;
int cnt=0;
for(int i=0;i<g[u].size();i++){
int v=g[u][i];
if(v==fa) continue;
if(!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(dfn[u]<low[v]){
ans++;
}
}
else{
low[u]=min(low[u],dfn[v]);
}
}
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
g[u].push\_back(v);
g[v].push\_back(u);
}
for(int i=1;i<=n;i++){
if(dfn[i]==0){
tarjan(i,0);
}
}
cout<<ans;
return 0;
}后话：
拜拜。
原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。
如有侵权，请联系 cloudcommunity@tencent.com 删除。
原创声明：本文系作者授权腾讯云开发者社区发表，未经许可，不得转载。
如有侵权，请联系 cloudcommunity@tencent.com 删除。
评论
登录后参与评论
推荐阅读
目录
腾讯云开发者
Copyright © 2013 - 2026 Tencent Cloud. All Rights Reserved. 腾讯云 版权所有
深圳市腾讯计算机系统有限公司 ICP备案/许可证号：粤B2-20090059 
粤公网安备44030502008569号
腾讯云计算（北京）有限责任公司 京ICP证150476号 | 京ICP备11018762号